ĐỀ THI THỬ ĐẠI HỌC Ngày 16 tháng 3 năm 2013
PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7.0 điểm)
Câu I (2.0 điểm) ) Cho hàm số
x 2
y
x 1
, có đồ thị (C).
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số
2. Viết phương trình tiếp tuyến của đồ thị (C), biết tiếp tuyến tạo với hai đường tiệm cận của
(C) một tam giác có bán kính đường tròn nội tiếp lớn nhất.
Câu II (2.0 điểm)
1. Giải phương trình:
25x x
4 3sin x cos x 2cos cos 3 sin 2x 3cos x 2
2 2
0
2sin x 3
2. Giải hệ phương trình:
2
2
y 1
x 3y 2 y 4x 2 5y 3x
3
3 6.3 3 2.3
1 2. x y 1 3. 3y 2x
Câu III (1.0 điểm) Tính tích phân:
1
x
2 2
3
4
e x
x 2tan x dx
x cos x
Câu IV (1.0 điểm) Cho hình chóp S.ABCD có đáy ABCD là hình thoi tâm O; AC =
2a 3
, BD = 2a;
hai mặt phẳng (SAC) và (SBD) cùng vuông góc với mặt phẳng (ABCD). Biết khoảng cách từ điểm O
đến mặt phẳng (SAB) bằng
a 3
4
, tính thể tích khối chóp S.ABCD theo a.
Câu V (1.0 điểm) Cho a, b, c là các số thực dương có tổng bằng 1. Chứng minh rằng:
3
1 1 1 10
a b c
b c a 3
PHẦN RIÊNG ( 3.0 điểm) (Thí sinh chỉ được làm một trong hai phần A hoặc B ).
A.Theo chương trình chuẩn:
Câu VI.a (2.0 điểm)
1. Trong mặt phẳng với hệ toạ độ Oxy, cho hình thoi MNPQ có M(1; 2), phương trình NQ là
x y 1 0
. Tìm toạ độ các đỉnh còn lại của hình thoi, biết rằng NQ = 2MP và N có tung độ âm.
2. Trong không gian với hệ trục tọa độ vuông góc Oxyz, cho điểm
I 1;1;1
. Viết phương trình mặt
phẳng
P
qua I cắt các trục tọa độ Ox, Oy, Oz lần lượt tại A, B, C sao cho I là tâm đường tròn ngoại
tiếp tam giác ABC.
CâuVII.a (1.0 điểm) Cho khai triển:
2
10
2 2 14
o 1 2 14
1 2x x x 1 a a x a x ... a x
. Hãy tìm giá
trị của
6
a
.
B. Theo chương trình nâng cao:
Câu VI.b (2.0 điểm)
1. Trong mặt phẳng với hệ trục tọa độ vuông góc Oxy, cho hình bình hành ABCD tâm I, biết A(0;
1) và B(3; 4) thuộc parabol
2
P : y x 2x 1,
điểm I nằm trên cung AB của (P) sao cho tam giác
IAB có diện tich lớn nhất. Tìm tọa độ C và D.
2. Trong không gian với hệ trục tọa độ Oxyz, viết phương trình mặt phẳng (P) đi qua O, vuông
góc với mặt phẳng (Q):
5x 2y 5z 0
và tạo với mặt phẳng (R):
x 4y 8z 6 0
góc
o
45
.
CâuVII.b (1.0 điểm) Cho khai triển đa thức:
2013
2 2013
o 1 2 2013
1 2x a a x a x ... a x
. Tính tổng:
0 1 2 2013
S a 2 a 3 a ... 2014 a
...............................................HẾT...............................................
HƯỚNG DẪN GIẢI
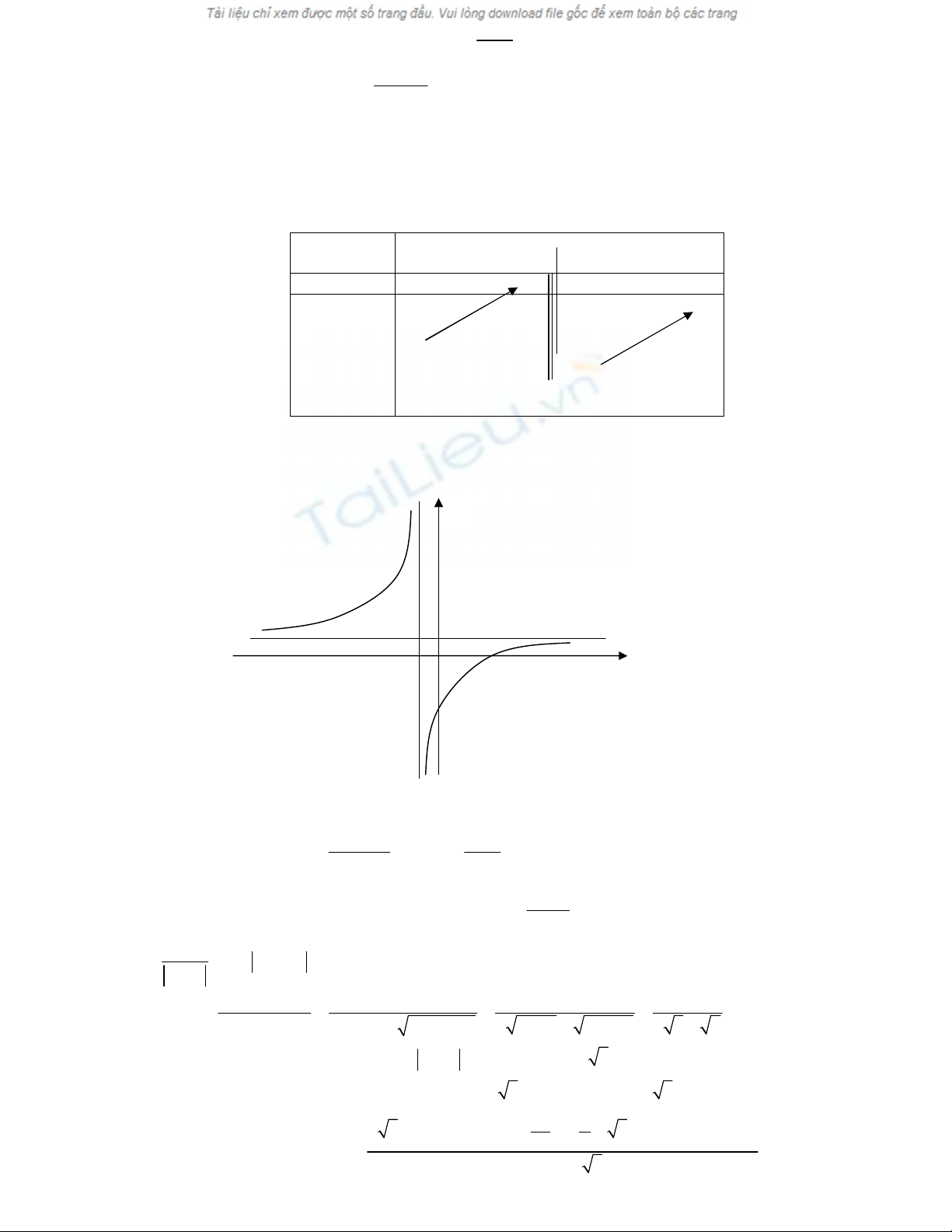
Câu 1: 1, Khảo sát sự biến thiên của hàm số
x 2
y
x 1
, có đồ thị (C).
* Tập xác định: D
\ 1
R
,
2
3
y 0, x D
x 1
* Sự biến thiên:
+ Giới hạn: xx 1 x 1
x
lim y lim y 1, lim y , lim y


 
.
Đồ thị (C) có tiệm cận ngang là đường thẳng y=1, tiệm cận đứng là đường thẳng x=-1
+ Bảng biến thiên:
x -
-1
+
y’ + +
y
+
1
1 -
+ Hàm số đồng biến trên khoảng
; 1

và
1;

.
* Đồ thị:
Đồ thị cắt trục tung tại điểm (0;-2), cắt trục hoành tại điểm (0; 2).
Đồ thị (C) nhận giao điểm hai tiệm cận I(-1; 1) làm tâm đối xứng
Câu 1: 2, Viết phương trình tiếp tuyến của đồ thị (C……..
PT tiếp tuyến d có dạng
o
2
o
3 x 2
y x x
x 1
x 1
, (với
o
x
là hoành độ tiếp điểm)
Giao điểm của d lần lượt với tc đứng, tc ngang là: o
o
x 5
A 1; ;
x 1
o
B 2x 1;1
o
o
6
IA ;IB 2x 2 IA.IB 12
x 1
Bán kính 2 2
IA.IB IA.IB IA.IB 6
rIA IB AB
2 IA.IB 2IA.IB 2 3 6
IA IB IA IB
Dấu “=” xảy ra khi và chỉ khi 2
o o
IA IB x 1 3 x 1 3
Vậy phương trình tiếp tuyến cần tìm là:
y x 2 2 3
hoặc
y x 2 2 3
Câu 2: 1, Giải phương trình :
25x x
4 3sin x cos x 2cos cos 3 sin 2x 3cosx 2
2 2
0
2sin x 3
y
I
-1 O
2
-
2
1 x
Điều kiện :
3
sin x
2
Phương trình đã cho tương đương với phương trình:
2 2
2
2
2 3sin 2xcosx cos3x cos2x 3sin 2x 3cosx 2 0
3sin 2x 2cosx 1 cos3x cosx cos2x 1 2cosx 1 0
3sin 2x 2cosx 1 4cosx.sin x 2sin x 2cos x 1 0
3sin 2x 2cos x 1 2sin x 2cos x 1 2cos x 1 0
2cos x 1 3sin 2x 2sin x 1 0 2cos x 1 3si
n 2x cos2x 2 0
12
cosx x 2k
2cosx 1 0 23k
3sin 2x cos2x 2 0 cos 2x 1 x k
36
Đối chiếu điều kiện ta được nghiệm của phương trình là: 2
x k ;x k2 ;x k2 (k Z)
3 3
Câu 2: 2, Giải hệ phương trình :
2
2
y 1
x 3y 2 y 4x 2 5y 3x
3
3 6.3 3 2.3
1 2. x y 1 3. 3y 2x
1
2
Đk:
x y 1 0
(*)
2 2
2
4x 2 3y 3x y 4x 2 2y 3y 3x y 1 2y
4x 2 2y y x y 4x 2 2y
1 3 6.3 3 2.3 0
3 3 27 6.3 0 3 3 0 y 2x 1
Thay vào (2) ta có: 3
2
1 2 3x 2 3. 4x 3,x
3
Đặt 3
a 3x 2 0;b 4x 3
ta có hệ 2 3
1 2a 3b
4a 3b 1
3
4
Từ
3b 1
3 a
2
thay vào pt (4) ta được 3 2
1
b 0 a
2
3b 9b 6b 0 b 1 a 1
5
b 2 a
2
+)
1
b 0;a
2
không thõa mãn +)
a 1 x 1
b 1 y 1
+)
11
5x
a
4
2
9
b 2 y
2
Kết hợp đk (*) suy ra hệ có nghiệm (x; y) là
11 9
1;1 , ;
9 2
Câu 3: Tính tích phân:
1
x
2 2
3
4
e x
x 2tan x dx
x cos x
Ta có:
112
xx
2 2 2 2
3 3 3 3
4 4 4 4
e x 1 x
I x 2tan x dx e . dx dx 2x tan xdx
x cos x x cos x
(1)