
SỞ GD&ĐT VĨNH PHÚC
TRƯỜNG THPT TAM DƯƠNG
ĐỀ KHẢO SÁT CHUYÊN ĐỀ LẦN 1 NĂM HỌC 2011 - 2012
MÔN: TOÁN 12 KHỐI A
Thời gian làm bài: 180 phút, không kể thời gian phát đề
Câu I (2,0 điểm) Cho hàm số
2 1
1
x
yx
1. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số trên.
2. Tìm trên đồ thị (C) những điểm M sao cho tiếp tuyến tại M tạo với hai đường tiệm cận
của đồ thị (C) một tam giác với đường tròn ngoại tiếp có bán kính bằng
2
.
Câu II (2,0 điểm)
1. Giải phương trình
2
2cos3 cos 3(1 sin 2 ) 2 3 cos 2 4
x x xx
.
2. Giải hệ phương trình
2 2
2
4 1
2
1
x y xy y
y
x y x
Câu II (2,0 điểm)
1. Tính giới hạn
234
2
( 3 9). 1 2 3
lim 2
x
x x x x
x
2. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
2
1 9 6 3
y x x x
Câu IV (2,0 điểm)
1. Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. Biết AB = 2a,
AD = CD = a,SA = 3a (a > 0) và SA vuông góc với mặt phẳng đáy. Tính thể tích khối chóp
S.BCD và tính khoảng cách từ điểm B đến mặt phẳng (SCD) theo a.
2. Cho các sốa,b,c dương thoả mãn
2 2 2 12
abc
.
Tìm giá trị nhỏ nhất của biểu thức:
333
1 1 1
1 1 1
Pabc
Câu V (2,0 điểm)
1. Cho phương trình
42
1 4 3 2 ( 3) 2 0
x m x x m x
.
Tìm m để phương trình có nghiệm thực.
2. Trong mặt phẳng với hệ toạ độ Oxy, cho hình vuông ABCD có M là trung điểm của
cạnh BC, phương trình đường thẳng DM:
2 0
x y
và điểm C(3;3). Biết đỉnh A thuộc
đường thẳng (d): 3x + y 2 = 0 và A có hoành độ âm. Xác định toạ độ các đỉnh A,B,D.
HẾT
Cán bộ coi thi không giải thích gì thêm!
Họ và tên thí sinh:......................................................... ..............................SBD:...................
www.laisac.page.tl
HƯỚNG DẪN CHẤM VÀ THANG ĐIỂM MÔN TOÁN 12 KHỐI A
C©u
Néi dung
§iÓm
1. TXĐ:
\{1}
+ Sự biến thiên:
Giới hạn và tiệm cận:
2 1 2 1
lim lim 2; lim lim 2
11
x x x x
xx
yy
xx
y = 2 là tiệm cận ngang.
1 1 1 1
2 1 2 1
lim lim ; lim lim
11
x x x x
xx
yy
xx
x = 1 là tiệm cận đứng.
2
1
' 0 ( ;1) (1; )
( 1)
yx
x
0,25
BBT
x
∞
1
+∞
y'
0
1
+∞
y
∞
1
Hàm số nghịch biến trên: (; 1) và (1; +)
0,5
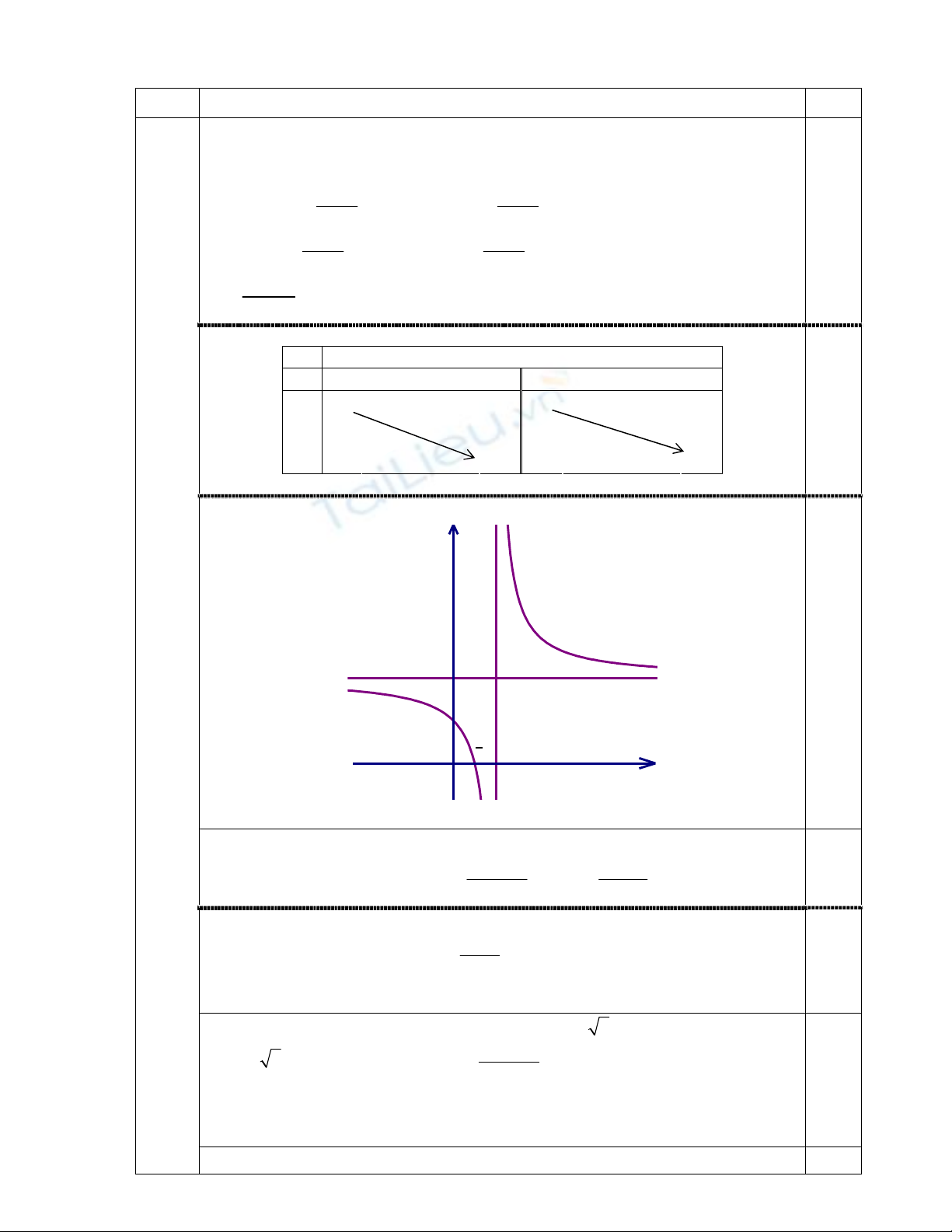
§å thÞ:
1
2
1
2
1
x
y
O
Đồ thị (C) nhận điểm I(1; 2) làm tâm đối xứng
0,25
2. Giả sử
0 0
( ; )
M x y
thuộc đồ thị (C) của hàm số.
Phương trình tiếp tuyến tại M là
0
0
20
0
2 1
1( ) 1
( 1)
x
y x x x
x
0,25
Gọi A,B lần lượt là giao điểm của tiếp tuyến với các đường tiệm cận của (C)
Giao với đường thẳng x = 1 là
0
0
2
1; 1
x
Ax
Giao với đường thẳng y = 2 là
0
2 1;2
B x
0,25
Vì bán kính đường tròn ngoại tiếp tam giác IAB bằng
2
nên
22
02
0
0
422
0000
4
2 2 8 (2 2) 8
( 1)
0
( 1) 2( 1) 1 0 ( 1) 1 2
AB AB x x
x
x x xx
0,5
I
Vậy có hai điểm cần tìm là
12
(0; 1), (2; 3)
M M

1. Phương trình tương đương
2cos3 cos 3(1 sin 2 ) 3 1 cos 4 2
x x xx
0,25
2cos3 cos 3(1 sin 2 ) 3(1 sin 4 )
2cos3 cos 3(sin 4 sin 2 ) 0
2cos3 cos 2 3 sin 3 cos 0
x x xx
x x x x
x x x x
0,25
cos 0 2
cos (cos3 3 sin 3 ) 0 1
tan 3 318 3
xx k
x x x xk
x
Vậy phương trình có hai nghiệm là:
2
x k
và
( )
18 3
k
xk
0,5
2. Nhận xét y = 0 không là nghiệm của hệ phương trình.
Hệ tương đương với:
2
2
14
2
1
xx y
y
y
x y x
0,25
Đặt
21,
x
u v x y
y
. Hệ phương trình có dạng
4
12
u v
vu
0,25
Giải hệ phương trình ta có: u = 1, v = 3
0,25
II
Với
21
11 2
1,
32 5
3
x
ux x
y
vy y
x y
0,25
1. Xét hàm số
2343
( ) ( 3 9) 1 2 3; 2
f x x x x x x
ta có:
(2) 0
f
và
2
3
22
34
3 9 1 41
'( ) 2 3 1 '(2) 6
3 ( 1) 2 (2 3)
x x
f x x x f
xx
0,5
Khi đó giới hạn cần tìm được viết dưới dạng:
2
( ) (2) 41
lim '(2)
26
x
f x f
If
x
0,5
III
2. TXĐ: D = [1; 3]
2
22
3 3 9 6 3 3 3
' 1
9 6 3 9 6 3
xx x x
y
x x x x
2
22
3 3 0
' 0 9 6 3 3 3 0 2
9 6 3 (3 3)
x
yx x x x
x x x
0,5
Ta có f (1) = 0; f (2) = 6; f (3) = 4
Vậy
[ 1;3]
[ 1;3]
max 6; min 0;
y y
0,25
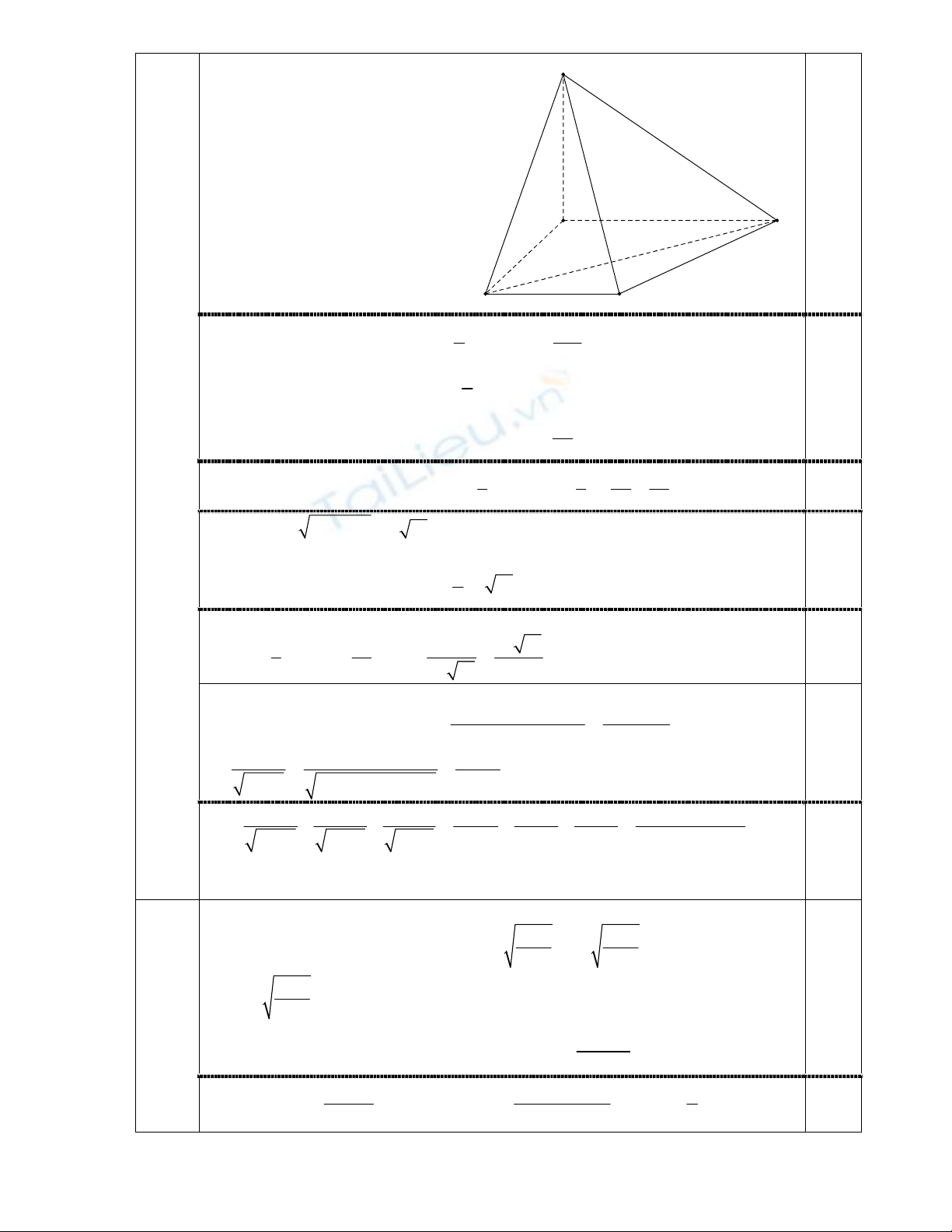
D
C
B
A
S
Diện tích hình thang ABCD là
2
13
(2 ).
22
a
S a a a
;
Diện tích tam giác ABD là
2
1.
2
ABD
S AB AD a
Diện tích tam giác BCD là
2
2
BCD ABD
a
S S S
0,25
Thể tích khối chóp S.BCD là
2 3
11
. 3 .
33 2 2
SBCD BCD
a a
V SA S a
0,25
Ta có:
2 2
910
SD a a a
Vì SA (ABCD)SA CD;AD CD CD SD.
Diện tích tam giác SCD là
2
110
2
SCD
S a
0,25
Gọi d là khoảng cách từ B đến mặt phẳng (SCD). Ta có
33
2
13 3 10
.
3 2 10
10
SBCD SCD
a a a
V d S da
0,25
Ta có:
22
22
321 1 2
1 (1 )(1 ) 44
a a a a
a a a a
2
32
112
2
1 (1 )( 1) a
a a a a
0,5
IV
Vậy
2 2 2 2 2 2
3 3 3
1 1 1 2 2 2 18 1
2 2 2 6
1 1 1 a b c a b c
abc
Dấu đẳng thức xảy ra khi và chỉ khi a = b = c = 2
Vậy GTNN của biểu thức làP = 1
0,5
1. ĐK: x≥ 2. Nhận xét x = 2 không là nghiệm của phương trình.
Với x > 2 phương trình tương đương với:
4
1 1
43 0
2 2
x x
m m
x x
Đặt
41, 1
2
x
t t
x
.
Phương trình có dạng
2
23
4 3 0 ( )
4 1
t
t mt m m f t
t
(t > 1)
0,25
V
Khảo sát
23
( ) 4 1
t
f t t
với t> 1,
2
2
4 2 12 3
'( ) 02
(4 1)
t t
f t t
t
,
0,25

Từ BBT ta có: phương trình có nghiệm
1;
3 3
max ( ) ( )
2 4
m f t f
0,5
2. Gọi
( ; 3 2) ,( )
A t t d t
. Ta có:
( , ) 2 ( , )
d A DM d C DM
4 4 2.4 3 1
2 2
tt t
hay A(3; 7) hoặc A(1; 5).
Vì hoành độ điểm A âm nên A(1; 5)
0,25
Gọi D(m;m 2)
,( )
DM m
( 1; 7); ( 3; 1)
AD m m CD m m
Do tứ giác ABCD là hình vuông nên:
222 2
5 1
. 0 5
( 1) ( 7) ( 3) ( 1)
m m
DA DC m
DA DC m m m m
D(5; 3)
0,5
V
Vì
( 2; 6) ( 3; 1)
AB DC B
Kết luận: A(1; 5); B(3; 1); D(5; 3).
0,25












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



