1
Phng trình vi phân
Bài 8B
PGS. TS. NGUYN XUÂN THO
Chng 7
H PHI TUYN VÀ CÁC HIN TNG
§ 7.1. Nghim cân bng và tính n nh
• S n nh ca nghim kì d
1. t vn 
• i vi mt phương trình vi phân bt kì không phi luôn tìm ưc nghim
tưng minh
• Ngay c khi không tìm ưc nghim tưng minh thì vn cn nhn ưc
nhng thông tin có giá tr v nghim; chng hn như tính không b chn, b
chn, tun hoàn ca nghim, ... minh ho qua mt s ví d dưi ây
Ví d 1. Gi x(t) là nhit  ca mt vt th vi nhit  ban u x(0) = x
0
.
thi im t = 0 vt th ưc nhúng trong mt dung dch có nhit  không i
bng A. Theo nh lý làm ngui ca Newton thì
( )
dx
k x A
dt
= − −
(k > 0, k = const)
• S dng phương pháp tách bi!n, nhn ưc nghim
x(t) = A + (x
0
- A)e
-kt
rõ ràng rng lim ( )
t
x t A
→∞
=
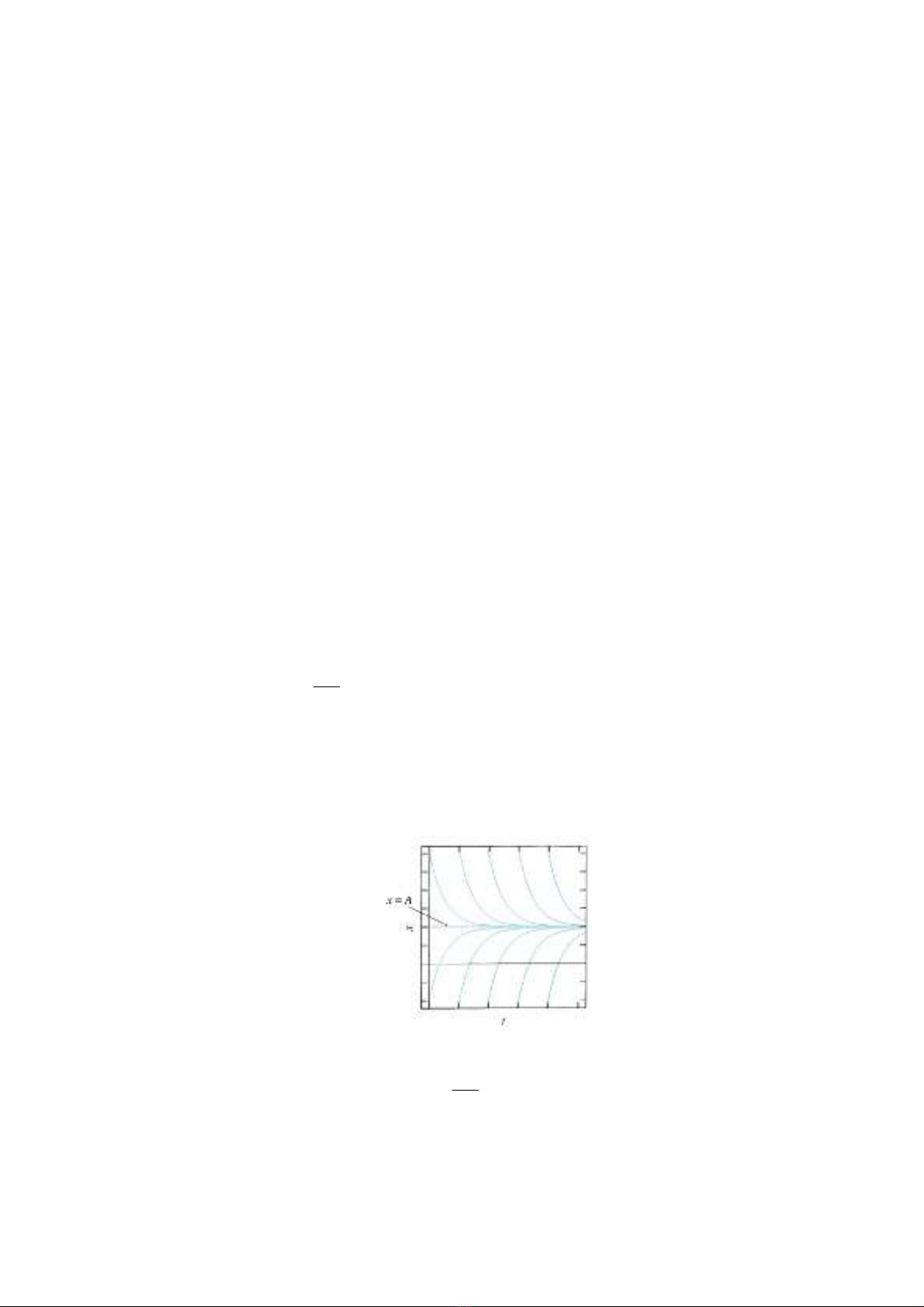
Hình 7.1.1. Các ưng cong nghim in hình ca phương trình làm ngui ca
Newton
( )
dx
k x A
dt
= − −
2
Ví d 2. Xét phương trình v t"ng trư#ng dân s
( )
dx
f x
dt =
# ó
(
f x
là t$ l sinh và t$ l t vong ca các cá th trong mt ơn v thi gian.
• ây là phương trình Otonom cp 1.
• N!u
(
)
=
0
f c thì có x(t) = c là nghim. Nghim hng s ca mt phương trình
vi phân còn ưc gi là nghim cân bng.
• Như vy c trưng nghim ca phương trình otonom cp 1 có th ưc mô t
qua các im k% d ca phương trình.
Ví d 3. Xét phương trình Logistic
( )
dx
kx M x
dt
= −
, # ó k > 0, M > 0.
• Có 2 im k% d, ó là các nghim x = 0 và x = M
• Có nghim (t& mc 1.7) là
0
0 0
( ) ( )
kMt
Mx
x t x M x e
−
=
+ −
• T& ó có
(
)
=
0
x t và
(
)
=
x t M
là nghim cân bng
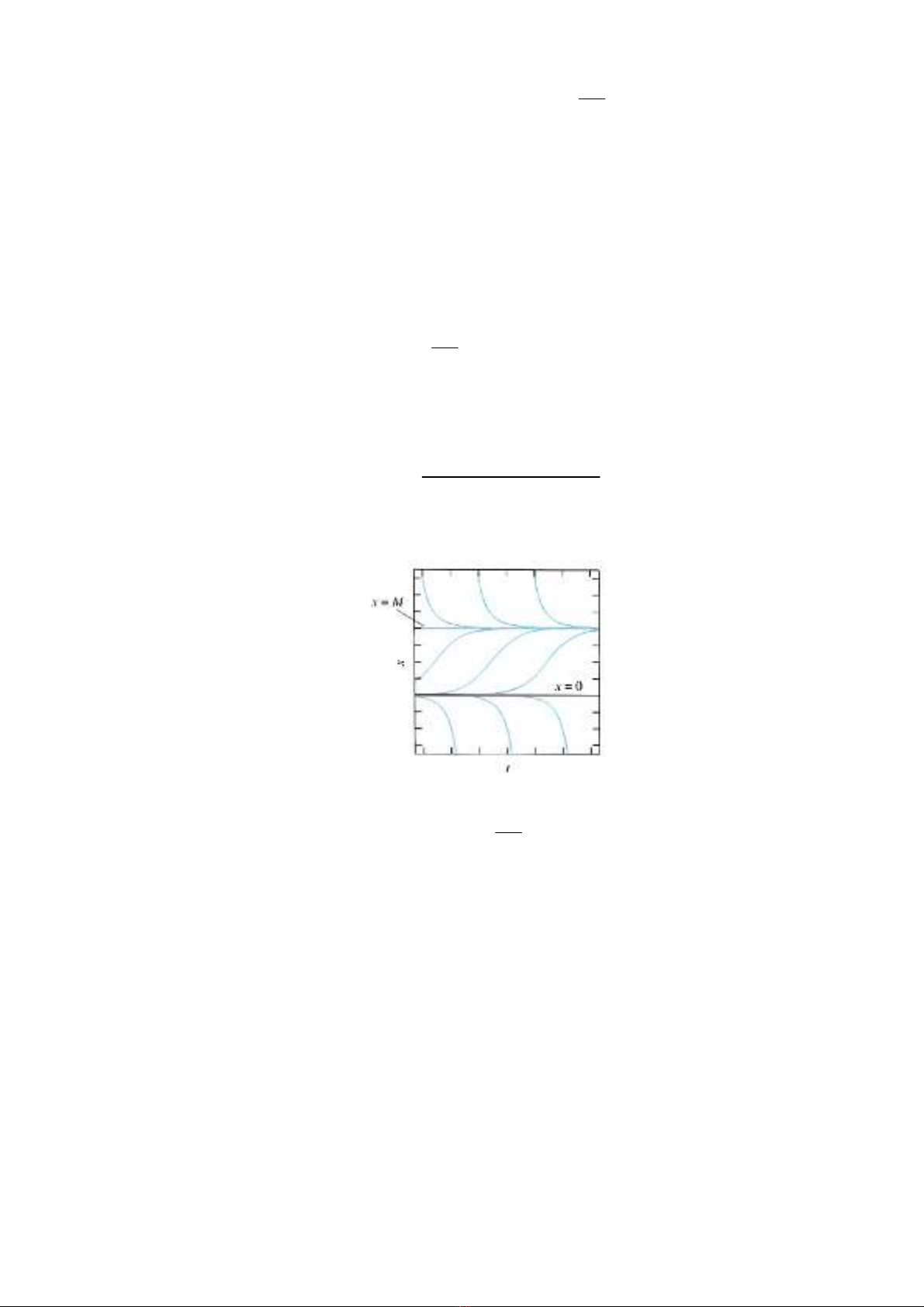
Hình 7.1.3. Các ưng cong nghim in hình
ca phương trình
( )
dx
kx M x
dt
= −
2. S n nh ca các im k d
• im k% d x = c ca 1 phương trình vi phân cp 1, otonom, ưc gi là n
nh n!u ∀ε > 0, ∃δ > 0 sao cho:
|x
0
-c| < δ thì có |x(t) - c| < ε, ∀t > 0.
• im k% d x = c ưc gi là không n nh, n!u nó không là im n nh.
3
Ví d 4.
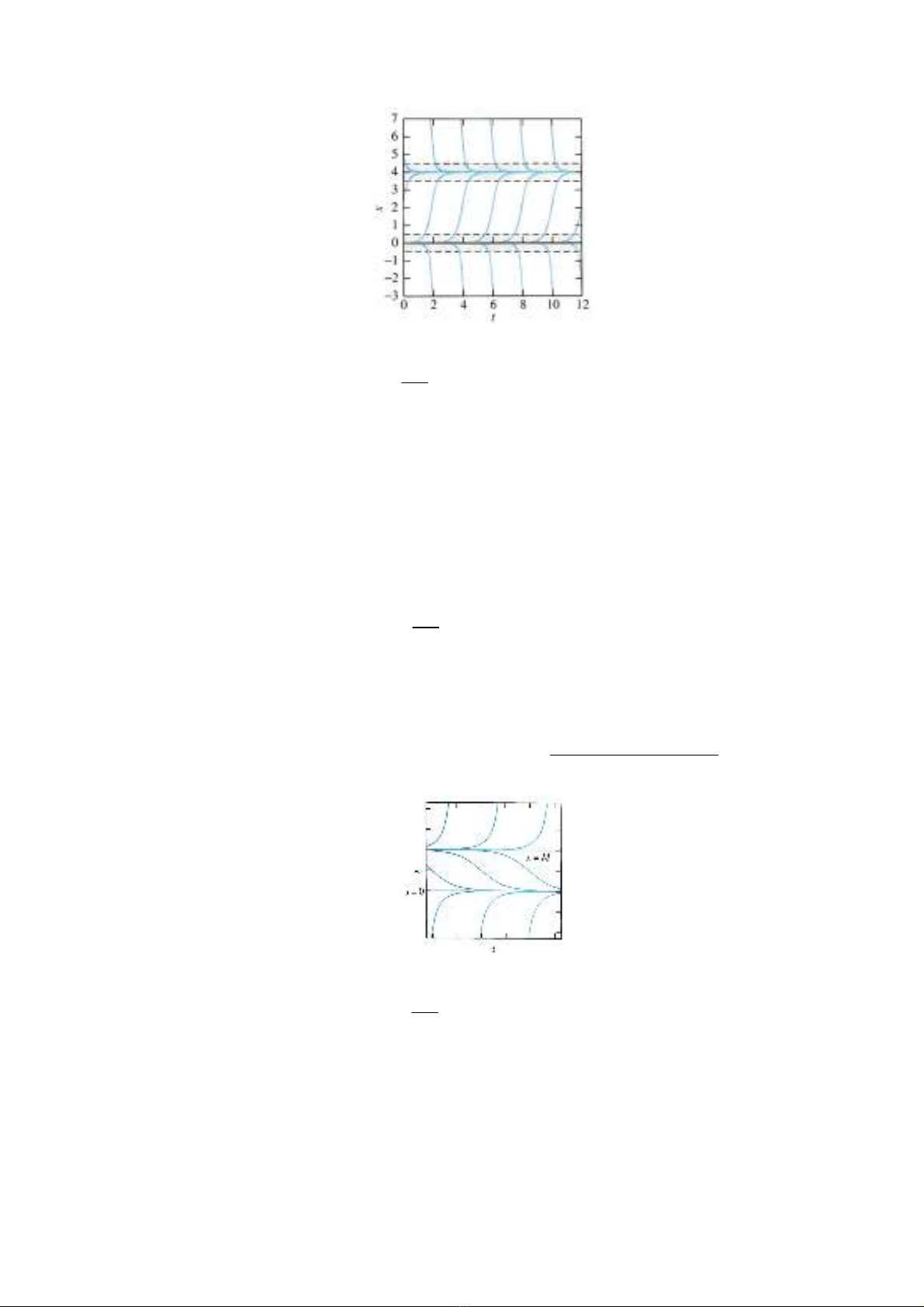
Hình 7.1.4. Các ưng cong nghim, ph'u và vòi ca phương trình
2
4
dx
x x
dt
= −
• Hình 7.1.4 cho cách nhìn "rng hơn" v ưng cong nghim ca mt phương
trình logistic vi k = 1 và M = 4. Chú ý rng di 3,5 < x < 4,5 (bao ly ưng x =
4) ging như cái ph'u ca các ưng cong nghim: khi di chuyn t& trái sang
phi thì các ưng cong nghim chui vào ph'u và # li trong ó. Ngưc li, di
-0,5 < x < 0,5 (bao ly ưng cong nghim không n nh x = 0) ging như 1 cái
vòi: các ưng cong nghim i vào di r(i sau ó i ra kh)i di. Vy im k% d
x = M = 4 là im n nh, còn im k% d x = 0 là im không n nh.
Ví d 5. Xét phương trình n/t*t
( )
dx
kx x M
dt = − ,
(
)
=
0
0
x x
.
• Có 2 im k% d là x = 0 và x = M tương +ng vi các nghim cân bng
x(t) = 0 và x(t) = M.
• Nghim tho mãn iu kin ban u là
0
0 0
( ) ( )
kMt
Mx
x t x M x e
=
+ −
Hình 7.1.6. Các ưng cong nghim in hình ca phương trình
( )
dx
kx x M
dt = −
• Mt di h,p quanh nghim n nh x = 0 ưc xem như mt cái ph'u, trong
khi mt di dc theo ưng cong nghim x = M ưc xem như mt cái vòi ca
các ưng cong nghim. Tính cht các nghim ca phương trình (9) ưc tóm
4
t*t b#i sơ ( pha # Hình 7.1.7. im k% d x = 0 là im n nh, còn im k% d
x = M là im không n nh.
Hình 7.1.7. Biu ( pha in hình ca phương trình
( )
( )
dx
f x kx x M
dt ==−
a) Bùng n dân s
Phương trình vi phân otonom
2
dx
ax bx h
dt
= − −
vi a > 0, b > 0, h > 0 ưc coi là phương trình mô t vic bùng n dân s.
Ví d 6. Xét phương trình vi phân
( )
dx
kx M x h
dt
= − −
(2.1)
• Phương trình này th hin s dân ti hn M khi h = 0 mà không có bùng n
dân s.
• Các im k% d ± −
=
2
( ) 4
,
2
kM kM hk
H N
k
• Gi s t$ l bùng n h  nh) sao cho 4h < kM
2
, khi ó các c"n ca H, N u
thc và khi 0 < H < N < M, ta vi!t li phương trình dưi dng:
( )( )
dx
k N x x H
dt
= − −
• Có nghim
( )
0 0 ( )
0 0
( ) ( )
( ) ( ) ( )
k N H t
k N H t
N x H H x N e
x t x H x N e
− −
− −
− − −
=
− − −
Hình 7.1.8. Các ưng cong nghim in hình ca phương trình
( )( )
dx
k N x x H
dt
= − −
• Vy ưng cong nghim ưc mô t như # Hình 7.1.8 (d' thy mt ph'u ca
nghim dc theo ưng x = N và mt vòi ca nghim dc theo ưng x = H).
5
Nghim hng x(t) = N là nghim ti hn cân bng, còn nghim hng x(t) = H là
nghim ngư-ng cân bng nghim này chia các nghim thành 2 nhánh: n!u x
0
>
H thì dân s t !n giá tr N, n!u x
0
< H thì dân s gim dn.
• im k% d n nh x = N và im k% d không n nh x = H, ưc mô t # sơ
( pha trong Hình 7.1.9
Hình 7.1.9. Sơ ( pha ca phương trình
( ) ( )( )
dx
f x k N x x H
dt = = − −
Ví d 7. Chúng ta xét mt +ng dng c th v các k!t lun n nh # ví d 6, vi
gi thi!t rng k = 1 và M = 4 vi lưng cá trong h( là x(t) g(m hàng tr"m ln
kim tra sau t n"m. Dù cá không b câu thì cui cùng trong h( vn còn khong
400 con, cho dù s cá ban du vi s lưng như th! nào. Bây gi, gi s h = 3
 cho hàng n"m thu hoch ưc 300 con (# m+c hng s qua các n"m), khi
ó phương trình (2.1) tr# thành
(4 ) 3
dx x x
dt
= − −
, và phương trình bc 2:
-x
2
+ 4x - 3 = 0 = (3 - x).(x - 1) = 0
có các nghim là H = 1, N = 3. Do vy lưng cá ngư-ng cân bng là 100 con và
ngư-ng ti hn cân bng là 300 con. Tóm li, n!u trong h( ban u có hơn 100
con, thì s cá s. t giá tr ti hn 300 con khi thi gian t t"ng lên. Nhưng n!u
lưng cá ban u trong h( ít hơn 100 con, thì h( s. b "câu h!t" và s lưng cá
s. h!t sau mt khong thi gian hu hn.
b) S r nhánh và tính c lp các tham s
• Mt h sinh hc hoc mt h vt lý, ưc c trưng b#i mt phương trình vi
phân, s. ph thuc rt nhiu vào giá tr ca các h s hay các tham s có mt
trong phương trình. Chng hn, s lưng các im k% d ca mt phương trình
vi phân có th b thay i t ngt khi thay i giá tr ca mt tham s.
Ví d 8. Phương trình vi phân
(4 )
dx
x x h
dt
= − −
(x có giá tr hàng tr"m) c trưng cho s bùng n dân s (2.1) khi k = 1 và cho
s dân ti hn khi M = 4. Trong Ví d 7, chúng ta ã xét trưng hp h = 3 và
thy rng ngư-ng ti hn cân bng là N = 300 và s dân ngư-ng cân bng là
H = 100. Các ưng cong nghim in hình, bao g(m c các nghim cân bng
x(t) = 3 và x(t) = 1, ưc mô t # Hình 7.1.8.
• Khi k = 1 và M = 4, dân s ti hn N và s dân t ngư-ng H là
1
, (4 16 4 ) 2 4
2
H N h h
= ± − = ± −
(2.2)