Tài liu luyn thi ði hc Cơ hc vt rn toàn tp Trn Th An (havang1895@gmail.com – 09.3556.4557) Trang 1
CHUYN ðNG QUAY CA VT RN QUANH MT TRC C ðNH
A. TÓM TT KIN THC CƠ BN
1. To" ñ$ góc
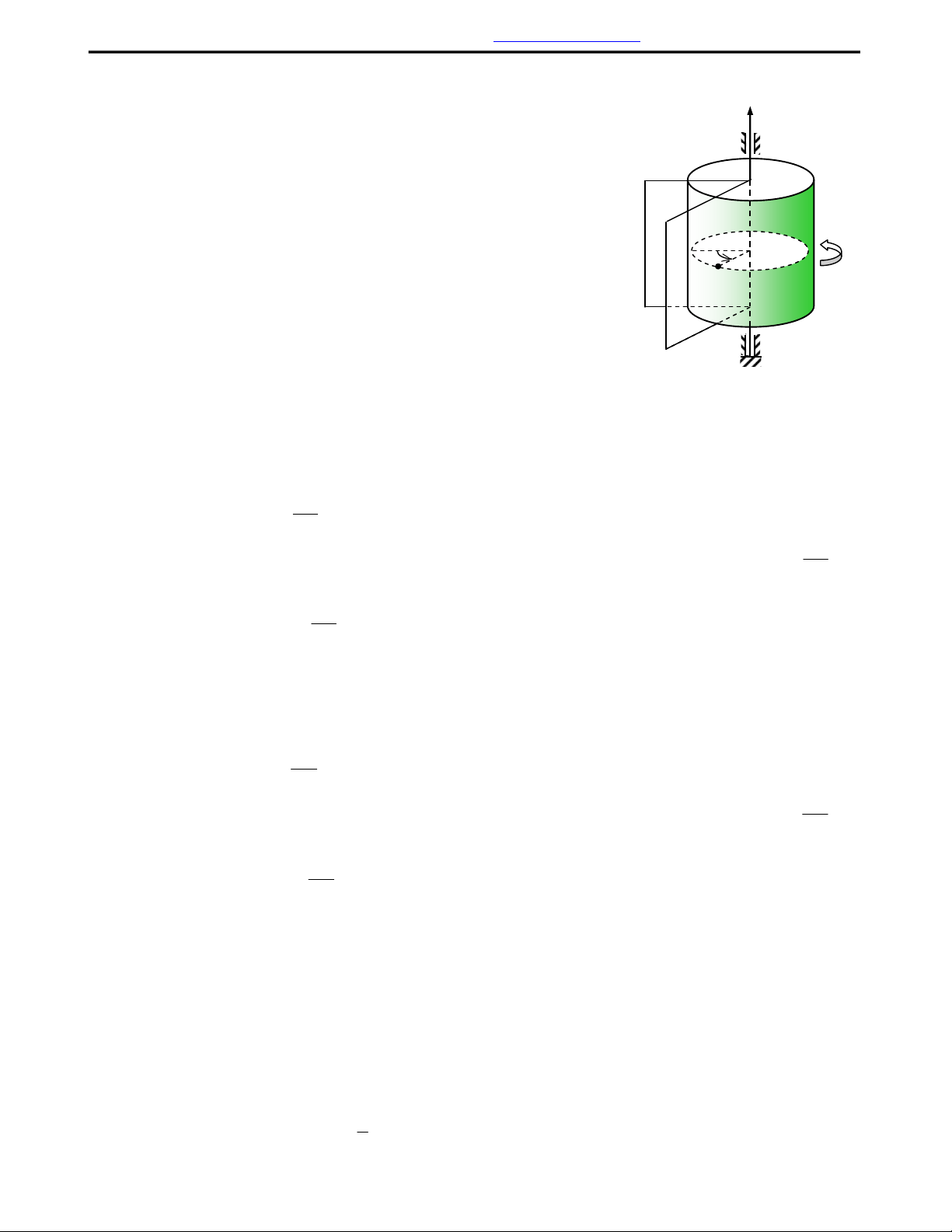
Khi vt rn quay quanh mt trc c ñnh (hình 1) thì :
Mi ñim trên vt v ch mt ñư"ng tròn n%m trong m't ph)ng vuông
góc v,i trc quay, có bán kính r b%ng kho2ng cách t3 ñim ñó ñ4n trc
quay, có tâm O 6 trên trc quay.
M8i ñim c9a vt ñ:u quay ñư;c cùng mt góc trong cùng mt
kho2ng th"i gian.
Trên hình 1, v trí c9a vt t i mi th"i ñim ñư;c xác ñnh b%ng góc φ
gi?a mt m/t ph0ng ñ2ng P gn v,i vt và mt m/t ph0ng c4 ñ5nh P
0
(hai
m't ph)ng này ñ:u chAa trc quay Az). Góc φ ñư;c g8i là to ñ2 góc c9a
vt. Góc φ ñư;c ño b%ng rañian, kí hiFu là rad.
Khi vt rn quay, sH bi4n thiên c9a φ theo th"i gian t th hiFn quy lut
chuyn ñng quay c9a vt.
2. T)c ñ$ góc
Tc ñ góc là ñ i lư;ng ñ'c trưng cho mAc ñ nhanh chm c9a chuyn ñng quay c9a vt rn.
J th"i ñim t, to ñ góc c9a vt là φ. J th"i ñim t + 9t, to ñ góc c9a vt là φ + 9φ. Như vy, trong
kho2ng th"i gian 9t, góc quay c9a vt là 9φ.
T4c ñ2 góc trung bình ω
tb
c9a vt rn trong kho2ng th"i gian 9t là :
t
tb
=
ϕ
ω
(1.1)
T4c ñ2 góc t=c th>i ω
6 th"i ñim
t
(g8i tt là tc ñ góc) ñư;c xác ñnh b%ng gi,i h n c9a tL s
t
ϕ
khi
cho
9t
dNn t,i 0. Như vy :
t
t
=
→
ϕ
ω
0
lim
hay )(
'
t
ϕω
= (1.2)
ðơn v c9a tc ñ góc là
rad/s
.
3. Gia t)c góc
T i th"i ñim
t
, vt có tc ñ góc là
ω
. T i th"i ñim
t + 9t
, vt có tc ñ góc là
ω + 9ω
. Như vy, trong
kho2ng th"i gian
9t
, tc ñ góc c9a vt bi4n thiên mt lư;ng là
9ω
.
Gia t4c góc trung bình γ
tb
c9a vt rn trong kho2ng th"i gian
9t
là :
t
tb
=
ω
γ
(1.3)
Gia t4c góc t=c th>i γ
6 th"i ñim
t
(g8i tt là gia tc góc) ñư;c xác ñnh b%ng gi,i h n c9a tL s
t
ω
khi
cho
9t
dNn t,i 0. Như vy :
t
t
=
→
ω
γ
0
lim hay )(
'
t
ωγ
=
(1.4)
ðơn v c9a gia tc góc là rad/s
2
.
4. Các phương trình ñ$ng h7c c8a chuy;n ñ$ng quay
a)
Trư"ng h;p tc ñ góc c9a vt rn không ñVi theo th"i gian (ω = h%ng s, γ = 0) thì chuyn ñng
quay c9a vt rn là chuyDn ñ2ng quay ñFu.
Ch8n gc th"i gian t = 0 lúc m't ph)ng P lFch v,i m't ph)ng P
0
mt góc φ
0
, t3 (1) ta có :
φ = φ
0
+ ωt (1.5)
b)
Trư"ng h;p gia tc góc c9a vt rn không ñVi theo th"i gian (γ = h%ng s) thì chuyn ñng quay c9a
vt rn là chuyDn ñ2ng quay bin ñHi ñFu.
Các phương trình c9a chuyn ñng quay bi4n ñVi ñ:u c9a vt rn quanh mt trc c ñnh :
t
γ
ω
ω
+
=
0
(1.6)
2
00
2
1tt
γωϕϕ
++=
(1.7)
)(2
0
2
0
2
ϕϕγωω
−=−
(1.8)
P
0
P
A
z
Hình 1
φ
r
O

Tài liu luyn thi ði hc Cơ hc vt rn toàn tp Trn Th An (havang1895@gmail.com – 09.3556.4557) Trang 2
trong ñó φ
0
là to ñ góc t i th"i ñim ban ñNu t = 0.
ω
0
là tc ñ góc t i th"i ñim ban ñNu t = 0.
φ là to ñ góc t i th"i ñim t.
ω là tc ñ góc t i th"i ñim t.
γ là gia tc góc (γ = h%ng s).
N4u vt rn chL quay theo mt chi:u nhbt ñnh và tc ñ góc tăng dNn theo th"i gian thì chuyn ñng
quay là nhanh dn. Khi ñó γ và ω mang cùng dbu.
N4u vt rn chL quay theo mt chi:u nhbt ñnh và tc ñ góc gi2m dNn theo th"i gian thì chuyn ñng
quay là chm dn. Khi ñó γ và ω mang khác dbu.
5. V@n t)c và gia t)c c8a các ñi;m trên v@t quay
Tc ñ dài v c9a mt ñim trên vt rn liên hF v,i tc ñ góc ω c9a vt rn và bán kính qud ñ o r c9a
ñim ñó theo công thAc :
r
v
ω
=
(1.9)
N4u vt rn quay ñFu thì mi ñim c9a vt chuyn ñng tròn ñ:u. Khi ñó vectơ vn tc
v
c9a mi ñim
chL thay ñVi v: hư,ng mà không thay ñVi v: ñ l,n, do ñó mi ñim c9a vt có gia tc hư,ng tâm
n
a
v,i ñ
l,n xác ñnh b6i công thAc :
r
r
v
a
n
2
2
ω
==
(1.10)
N4u
vt rn quay không ñFu
thì mi ñim c9a vt chuyn ñng tròn không ñ:u. Khi ñó vectơ vn tc
v
c9a mi ñim thay ñVi c2 v: hư,ng và ñ l,n, do ñó mi ñim c9a vt có gia tc
a
(hình 2) gfm hai thành
phNn :
+ Thành phNn
n
a
vuông góc v,i
v
,
ñc trưng cho s thay ñi v hưng
c9a
v
, thành phNn này chính là
gia t4c hưLng tâm
, có ñ l,n xác ñnh b6i công thAc :
r
r
v
a
n
2
2
ω
==
(1.11)
+ Thành phNn
t
a
có phương c9a
v
,
ñc trưng cho s thay ñi v ñ ln
c9a
v
, thành phNn này ñư;c
g8i là
gia t4c tip tuyn
, có ñ l,n xác ñnh b6i công thAc :
γ
r
t
v
a
t
=
=
(1.12)
Vectơ gia tc
a
c9a ñim chuyn ñng tròn không ñ:u trên vt là :
tn
aaa
+
=
(1.13)
V: ñ l,n :
22
tn
aaa +=
(1.14)
Vectơ gia tc a
c9a mt ñim trên vt rn h;p v,i bán kính OM c9a nó mt
góc
α
, v,i :
2
tan
ω
γ
α
==
n
t
a
a (1.15)
PHƯƠNG TRÌNH ðNG LIC HJC CA VT RN QUAY QUANH MT TRC C ðNH
A. TÓM TT KIN THC CƠ BN
1. M)i liên hL giMa gia t)c góc và momen lOc
a) Momen lOc ñ)i vPi m$t trQc quay c) ñRnh
Momen M c9a lHc
F
ñi v,i trc quay i có ñ l,n b%ng :
FdM
=
(2.1)
trong ñó d là tay ñòn c9a lHc
F
(kho2ng cách t3 trc quay i ñ4n giá c9a lHc
F
)
v
t
a
n
a
a
r
O
M
α
Hình 2

Tài liu luyn thi ði hc Cơ hc vt rn toàn tp Trn Th An (havang1895@gmail.com – 09.3556.4557) Trang 3
Ch8n chi:u quay c9a vt làm chi:u dương, ta có quy ư,c :
M > 0 khi
F
có tác dng làm vt quay theo chi:u dương
M < 0 khi
F
có tác dng làm vt quay theo chi:u ngư;c chi:u dương.
b)
M)i liên hL giMa gia t)c góc và momen lOc
S
Trư"ng h;p vt rn là mt qu2 cNu nhl có khi lư;ng m
gn vào mt ñNu thanh rbt nhm và dài r. Vt quay trên m't
ph)ng nhnn n%m ngang xung quanh mt trc i th)ng ñAng ñi
qua mt ñNu c9a thanh dư,i tác dng c9a lHc
F
(hình 1).
Phương trình ñng lHc h8c c9a vt rn này là :
γ
)(
2
mrM = (2.2)
trong ñó M là momen c9a lHc
F
ñi v,i trc quay i, γ là
gia tc góc c9a vt rn m.
Trư"ng h;p vt rn gfm nhi:u chbt ñim khi lư;ng m
i
, m
j
, … 6 cách trc quay i nh?ng kho2ng r
i
, r
j
,
… khác nhau.
Phương trình ñng lHc h8c c9a vt rn này là :
γ
=
∑
i
ii
rmM
2
(2.3)
2. Momen quán tính
Trong phương trình (2.3), ñ i lư;ng
2
i
i
i
rm
∑
ñ'c trưng cho mAc quán tính c9a vt quay và ñư;c g8i là
momen quán tính, kí hiFu là I.
Momen quán tính I ñi vi mt tr c là ñ"i lư#ng ñc trưng cho m$c quán tính c%a v&t r'n trong
chuy(n ñng quay quanh tr c )y.
2
i
i
i
rmI
∑
=
(2.4)
Momen quán tính có ñơn v là kg.m
2
.
Momen quán tính c9a mt vt rn không chL ph thuc khi lư;ng c9a vt rn mà còn ph thuc c2 vào
sH phân b khi lư;ng xa hay gNn trc quay.
Momen quán tính c9a mt s vt rn ñi v,i trc quay ñi qua khi tâm:
+ Thanh ñfng chbt có khi lư;ng
m
và
có ti4t diFn nhl so v,i chi:u
dài
l
c9a nó, trc quay i ñi qua trung ñim c9a thanh và vuông góc v,i
thanh (hình 2) :
2
12
1
mlI =
(2.5)
+ Vành tròn ñfng chbt có khi lư;ng
m (trT rUng có kh4i lưVng m)
, có bán
kính
R
, trc quay i ñi qua tâm vành tròn và vuông góc v,i m't ph)ng vành tròn
(hình 3) :
2
mRI
=
(2.6)
+ ðĩa tròn mlng (tr ñ'c) ñfng chbt có khi lư;ng
m
, có bán kính
R
, trc quay i ñi qua tâm ñĩa tròn và
vuông góc v,i m't ñĩa (hình 4) :
2
2
1mRI
=
(2.7)
+ Qu2 cNu ñ'c ñfng chbt có khi lư;ng
m
, có bán kính
R
, trc quay i ñi qua
tâm qu2 cNu (hình 5) :
2
5
2mRI
=
(2.8)
+ Qu2 cNu ñ'c rng có khi lư;ng
m
, có bán kính
R
, trc quay i ñi qua tâm
qu2 cNu
Hình1
O r
F
i
i
l
Hình 2
R
9
Hình 3
i
R
Hình 4
i
R
Hình 5

Tài liu luyn thi ði hc Cơ hc vt rn toàn tp Trn Th An (havang1895@gmail.com – 09.3556.4557) Trang 4
2
2
3
I mR
=
3. Phương trình ñ$ng lOc h7c c8a v@t rUn quay quanh m$t trQc
Phương trình ñ2ng lXc hc cYa vt rn quay quanh m2t trTc là :
γ
IM
=
(2.9)
I
: momen quán tính c9a vt rn ñi v,i trc quay i
M
: momen lHc tác dng vào vt rn ñi v,i trc quay i
γ : gia tc góc c9a vt rn trong chuyn ñng quay quanh trc i
4. Bài t@p ví dQ
Mt thùng nư,c khi lư;ng
m
ñư;c th2 xung gi4ng nh" mt s;i dây qubn quanh
mt ròng r8c có bán kính
R
và momen quán tính
I
ñi v,i trc quay c9a nó (hình 6).
Khi lư;ng c9a dây không ñáng k. Ròng r8c coi như quay tH do không ma sát quanh
mt trc c ñnh. Xác ñnh biu thAc tính gia tc c9a thùng nư,c.
Bài gi,i :
Thùng nư,c chu tác dng c9a tr8ng lHc
gm
và lHc căng
T
c9a s;i dây.
Áp dng ñnh lut II Newton cho chuyn ñng tnh ti4n c9a thùng nư,c, ta có :
maTmg
=
−
(1)
Ròng r8c chu tác dng c9a tr8ng lHc
gM
, ph2n lHc Q
c9a trc quay và lHc căng
'
T
c9a s;i dây (
T’ = T
).
LHc căng
'
T
gây ra chuyn ñng quay cho ròng r8c. Momen c9a lHc căng dây
'
T
ñi v,i trc quay c9a ròng r8c là :
TR
R
T
M
=
=
'
.
Áp dng phương trình ñng lHc h8c cho chuyn ñng quay c9a ròng r8c, ta có :
γ
ITR
=
(2)
Gia tc tnh ti4n
a
c9a thùng nư,c liên hF v,i gia tc góc
γ
c9a ròng r8c theo hF
thAc :
R
a
=
γ
(3)
T3 (2) và (3) suy ra :
2
R
Ia
R
I
T==
γ
(4)
Thay
T
t3 (4) vào (1), ta ñư;c :
ma
R
Ia
mg =−
2
Suy ra :
g
m
I
R
I
m
mg
a
+
=
+
=
2
2
R
1
1
(5)
MOMEN ðNG LƯYNG. ðNH LUT BO TOÀN MOMEN ðNG LƯYNG
A. TÓM TT KIN THC CƠ BN
1. Momen ñ$ng lư[ng
Momen ñng lư;ng
L
c9a vt rn trong chuyn ñng quay quanh trc là :
ω
IL
=
(3.1)
trong ñó
I
là momen quán tính c9a vt rn ñi v,i trc quay
ω
là tc ñ góc c9a vt rn trong chuyn ñng quay quanh trc
ðơn v c9a momen ñng lư;ng là kg.m
2
/s.
2. D"ng khác c8a phương trình ñ$ng lOc h7c c8a v@t rUn quay quanh m$t trQc
Phương trình ñng lHc h8c c9a vt rn quay quanh mt trc ñư;c vi4t dư,i d ng khác là :
t
L
M
=
(3.2)
trong ñó
M
là momen lHc tác dng vào vt rn
ω
IL
=
là momen ñng lư;ng c9a vt rn ñi v,i trc quay
L
là ñ bi4n thiên c9a momen ñng lư;ng c9a vt rn trong th"i gian
t
Hình 6
Q
gM
'
T
T
gm
H
ình
7. C
ác
l
Hc
t
ác
dng vào ròng r8c
và thùng nư,c.

Tài liu luyn thi ði hc Cơ hc vt rn toàn tp Trn Th An (havang1895@gmail.com – 09.3556.4557) Trang 5
3. ðRnh lu@t b^o toàn momen ñ$ng lư[ng
N/u tng các momen lc tác d ng lên mt v&t r'n (hay h3 v&t) ñi vi mt tr c b6ng không thì tng
momen ñng lư#ng c%a v&t (hay h3 v&t) ñi vi mt tr c ñó ñư#c b,o toàn.
⇔
=
0M
L =Iω = h^ng s4 (3.3)
+ Trư"ng h;p I không ñVi thì ω không ñVi : vt rn (hay hF vt)
ñAng yên ho'c quay ñ:u.
+ Trư"ng h;p I thay ñVi thì ω thay ñVi : vt rn (hay hF vt) có I gi2m thì ω tăng, có I tăng
thì ω gi2m (Iω = h%ng s hay I
1
ω
1
= I
2
ω
2
).
ðNG NĂNG CA VT RN QUAY QUANH MT TRC C ðNH
A. TÓM TT KIN THC CƠ BN
1. ð$ng năng c8a v@t rUn quay quanh m$t trQc c) ñRnh
ðng năng W
ñ
c9a vt rn quay quanh mt trc c ñnh là :
W
ñ
2
2
1
ω
I
=
(4.1)
trong ñó I là momen quán tính c9a vt rn ñi v,i trc quay
ω là tc ñ góc c9a vt rn trong chuyn ñng quay quanh trc
ðng năng W
ñ
c9a vt rn quay quanh mt trc c ñnh có th vi4t dư,i d ng :
W
ñ
I
L
2
2
= (4.2)
trong ñó
L
là momen ñng lư;ng c9a vt rn ñi v,i trc quay
I
là momen quán tính c9a vt rn ñi v,i trc quay
ðng năng c9a vt rn có ñơn v là jun, kí hiFu là J.
2. ðRnh lí bian thiên ñ$ng năng c8a v@t rUn quay quanh m$t trQc c) ñRnh
ð bi/n thiên ñng năng c%a mt v&t b6ng tng công c%a các ngo"i lc tác d ng vào v&t.
9W
ñ
=
AII =−
2
1
2
2
2
1
2
1
ωω
(4.3)






![Tài liệu ôn thi THPT Quốc gia Vật lý lớp 12 [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2024/20240403/vananh9a2kcr/135x160/5571712163061.jpg)








![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)




