Xác suất thống kê – Đề tham khảo 2 Trần Ngọc Hội
1
ĐỀ THAM KHẢO 2
MÔN: XÁC SUẤT THỐNG KÊ
THỜI GIAN LÀM BÀI: 90 PHÚT
(Được sử dụng tài liệu và máy tính)
(GV: Trần Ngọc Hội - 2009)
Câu 1. Có hai lô hàng: Lô I chứa rất nhiều sản phẩm với tỉ lệ loại tốt là 70%; Lô II
chứa 20 sản phẩm với tỉ lệ loại tốt là 60%. Lấy ngẫu nhiên 3 sản phẩm từ lô I bỏ sang
lô II, sau đó từ lô II chọn ra 4 sản phẩm. Tính xác suất để trong 4 sản phẩm chọn ra,
số tốt nhiều hơn số xấu.
Câu 2. Một máy sản xuất sản phẩm với tỉ lệ loại tốt là 60%. Sản phẩm được đóng
thành hai loại kiện gồm 30% kiện loại I và 70% kiện loại II. Mỗi kiện loại I chứa 6
sản phẩm; mỗi kiện loại II chứa 5 sản phẩm. Một kiện được xếp vào loại A nếu số tốt
nhiều hơn số xấu. Chọn ngẫu nhiên 200 kiện. Tính xác suất để
a) có 128 kiện loại A;
b) có từ 125 đến 160 kiện loại A.
Câu 3. Để khảo sát chỉ tiêu X của một loại sản phẩm, người ta quan sát một mẫu và
có kết qủa sau:
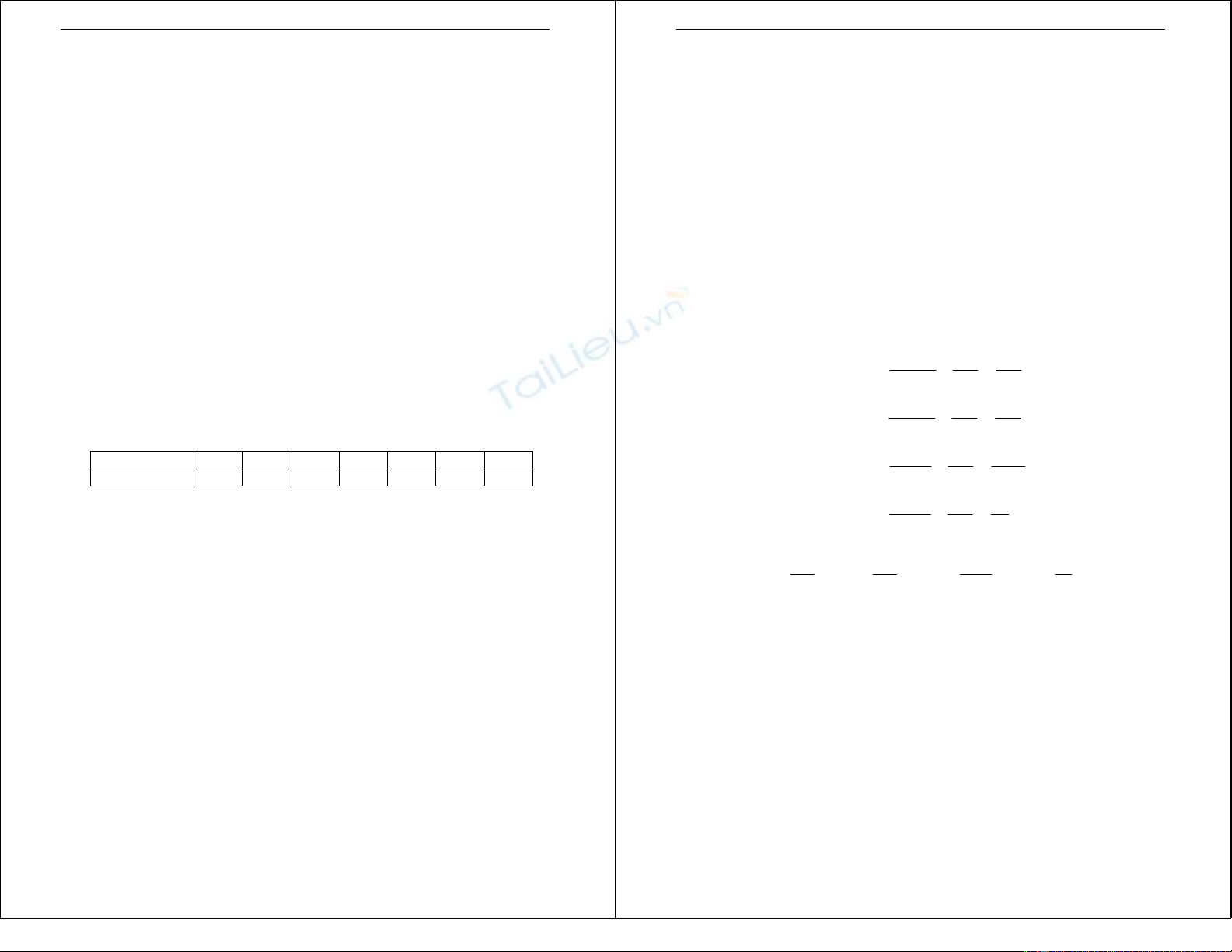
X(cm) 11−13 13−15 15−17 17−19 19−21 21−23 23−25
Số sản phẩm 12 14 30 29 18 16 12
a) Nếu muốn ước lượng giá trị trung bình của chỉ tiêu X với độ chính xác 0,6cm
thì sẽ đạt được độ tin cậy là bao nhiêu?
b) Những sản phẩm có chỉ tiêu X từ 17cm−23cm là những sản phẩm loại A. Ước
lượng tỉ lệ sản phẩm loại A với độ tin cậy 95%. Với độ tin cậy đó, nếu trong
kho có 1000 sản phẩm loại A thì tổng số sản phẩm có trong kho khoảng bao
nhiêu?
Câu 4. Một máy sản xuất sản phẩm với tỉ lệ loại tốt là 60%. Do sự cố về điện, máy bị
hỏng. Sau khi sửa chữa và cho máy hoạt động lại, người ta kiểm tra ngẫu nhiên 500
sản phẩm thì thấy có 275 sản phẩm tốt.
a) Với mức ý nghĩa 1%, tỉ lệ sản phẩm tốt do máy sản xuất có bị thay đổi không?
b) Với mức ý nghĩa 5%, có thể nói tỉ lệ sản phẩm tốt do máy sản xuất bị sụt giảm
đi hay không?
Xác suất thống kê – Đề tham khảo 2 Trần Ngọc Hội
2
Lời giải
Câu 1. Từ giả thiết ta suy ra lô II chứa 20 sản phẩm gồm 20.60% = 12 sản phẩm tốt
và 8 sản phẩm xấu.
Gọi A là biến cố số sản phẩm tốt nhiều hơn số xấu trong 4 sản phẩm chọn ra từ lô II.
Gọi Aj (j = 0, 1, 2, 3) là biến cố có j sản phẩm tốt và (3-j) sản phẩm xấu có trong 3 sản
phẩm lấy từ lô I. Khi đó A0, A1, A2, A3 là một hệ đầy đủ, xung khắc từng đôi và theo
công thức Bernoulli với n = 3 , p = 70% = 0,7, ta có:
003 3
03
112 1 2
13
221 2
23
330 3
33
p(A ) C p q (0, 3) 0, 027;
p(A ) C p q 3(0, 7) (0, 3) 0,189;
p(A ) C p q 3(0, 7) (0, 3) 0, 441;
p(A ) C p q (0, 7) 0, 343.
===
== =
== =
===
Theo công thức xác suất đầy đủ, ta có:
P(A) = P(A0)P(A/A0) + P(A1)P(A/A1) + P(A2)P(A/A2) + P(A3)P(A/A3).
Mặt khác, theo giả thiết, A xảy ra khi chọn được 3 tốt,1 xấu hoặc được 4 tốt, do đó
theo công thức Xác suất lựa chọn, ta có:
31 4
12 11 12
044
23 23
31 4
13 10 13
144
23 23
31 4
14 9 14
244
23 23
31 4
15 8 15
344
23 23
CC C 53
P(A / A ) ;
161
CC
CC C 65
P(A / A ) ;
161
CC
CC C611
P(A / A ) ;
1265
CC
CC C 13
P(A / A ) .
23
CC
=+=
=+=
=+=
=+=
Suy ra:
53 65 611 13
P(A) = 0,027 + 0,189 + 0,441 + 0,343 0, 4921.
161 161 1265 23 =
Kết luận: Xác suất để trong 4 sản phẩm chọn ra từ lô II, số sản phẩm tốt nhiều hơn số
sản phẩm xấu là 0,4921.
Câu 2. Trước hết ta cần tính xác suất p để một kiện thuộc loại A.
Chọn ngẫu nhiên một kiện. Gọi B là biến cố kiện thuộc loại A. Ta cần tính p = P(B).
Gọi A1, A2 lần lượt là biến cố kiện thuộc loại I, II. Khi đó A1, A2 là một hệ đầy đủ,
xung khắc từng đôi và giả thiết cho ta:
P(A1) = 30% = 0,3; P(A2) = 70% = 0,7.
Theo công thức xác suất đầy đủ, ta có:
P(B) = P(A1)P(B/A1) + P(A2)P(B/A2).
Mặt khác, theo giả thiết, kiện thuộc loại A nếu số tốt nhiều hơn số xấu. Do đó theo
công thức Bernoulli ta có:
Printed with FinePrint trial version - purchase at www.fineprint.com

Xác suất thống kê – Đề tham khảo 2 Trần Ngọc Hội
3
442 551 660
16 6 6
42 51 6
332 441 550
25 5 5
32 41 5
P(B / A ) C p q C p q C p q
15(0, 6) (0, 4) 6(0, 6) (0, 4) (0, 6) 0, 54432;
P(B/A ) Cpq Cpq Cpq
10(0, 6) (0, 4) 5(0, 6) (0, 4) (0, 6) 0, 68256.
=++
=++=
=++
=++=
Suy ra
P(B) = 0,3.0,54432 + 0,7.0,68256 = 0,641088.
Vậy xác suất để một kiện thuộc loại A là p = 0,641088.
Bây giờ, chọn ra 200 kiện. Gọi X là số kiện loại A có trong 200 kiện được chọn, thì X
có phân phối nhị thức X ∼ B(n,p) với n = 200, p = 0,641088. Vì n = 200 khá lớn và p
= 0,641088 không quá gần 0 cũng không quá gần 1 nên ta có thể xem X có phân phối
chuẩn như sau:
X ∼ N(μ, σ2)
Với μ = np = 200.0,641088 = 128,2176;
npq 200.0, 641088.(1 0, 641088) 6,7837σ= = − = .
a) Xác suất để có 128 kiện loại A là:
1 128 1 128 128, 2176
P (X 128) f ( ) f ( )
6,7837 6,7837
1 1 0, 3988
f ( 0, 03) f (0, 03) 0, 0588
6, 7837 6, 7837 6, 7837
−μ −
== =
σσ
=−= ==
(Tra bảng giá trị hàm Gauss ta được f(0,03) = 0,3988).
Vậy xác suất để có 128 kiện loại A là 5,88%.
b) Xác suất để có từ 125-160 kiện loại A là :
160 125
P(125 X 160) ( ) ( )
160 128, 2176 125 128,2176
()()
6,7837 6,7837
(4,685) ( 0,47) (4, 5) (0, 47)
0, 499997 0,1808 0, 6808.
−μ −μ
≤≤ =ϕ −ϕ
σσ
−−
=ϕ −ϕ
=ϕ −ϕ− =ϕ +ϕ
=+=
(Tra bảng giá trị hàm Laplace ta được ϕ(4,5) = 0,499997; ϕ(0,47) = 0,1808).
Vậy xác suất để có từ 125-160 kiện loại A là 68,08%.
Câu 3. Lập bảng
Xi 12 14 16 18 20 22 24
ni 12 14 30 29 18 16 12
Ta có:
n131;= ii
X
n 2342;=
∑ 2
ii
X n 43404.=
∑
• Kỳ vọng mẫu của X là
Xác suất thống kê – Đề tham khảo 2 Trần Ngọc Hội
4
ii
1
X X n 17, 8779(cm).
n
==
∑
• Phương sai mẫu của X là:
222 22
ii
1
S X n X (3, 4220) (cm ).
n
=−=
∑
• Phương sai mẫu đã hiệu chỉnh của X là:
2
222
n
S S (3, 4352) (cm ).
n1
==
−
a) Nếu muốn ước lượng giá trị trung bình của chỉ tiêu X với độ chính xác 0,6cm
thì sẽ đạt được độ tin cậy là bao nhiêu?
Yêu cầu của bài tóan: Xác định độ tin cậy γ = 1 − α.
Giả thiết: - Ước khỏang cho kỳ vọng của X.
- Độ chính xác ε = 0,6cm.
Vì n ≥ 30, σ2 = D(X) chưa biết nên ta có công thức tính độ chính xác của ước lượng:
S
zn
α
ε=
trong đó ϕ(zα) = (1− α)/2 = γ /2 . Suy ra
n0,6.131
z2,00
S 3, 4352
α
ε
== =
Tra bảng giá trị hàm Laplace ta được độ tin cậy là:
2 (z ) 2 (2, 00) 2.0, 4772 95, 44%.
α
γ
=ϕ =ϕ = =
Vậy độ tin cậy đạt được là 95,44%.
b) Những sản phẩm có chỉ tiêu X từ 17cm-23cm là những sản phẩm loại A. Ước
lượng tỉ lệ sản phẩm loại A với độ tin cậy 95%. Với độ tin cậy đó, nếu trong
kho có 1000 sản phẩm loại A thì tổng số sản phẩm có trong kho khoảng bao
nhiêu?
Đây là bài toán ước lượng khoảng cho tỉ lệ p các sản phẩm loại A với độ tin cậy γ
= 1 − α = 95% = 0,95. Ta có công thức ước lượng khoảng :
nn nn
nn
F(1 F) F(1 F)
(F z ; F z )
nn
αα
−−
−+,
trong đó ϕ(zα) = γ /2 = 0,95/2 = 0,475. Tra bảng giá trị hàm Laplace ta được zα =
1,96. Mặt khác, trong n =131 sản phẩm có m = 29 + 18 + 16 = 63 sản phẩm có chỉ
tiêu X từ 17cm-23cm nên số sản phẩm loại A có trong mẫu là m = 63. Suy ra tỉ lệ mẫu
sản phẩm loại A là Fn = m/n = 63/131 = 0,4809. Vậy ước lượng khoảng là:
0, 4809(1 0, 4809) 0, 4809(1 0, 4809)
(0, 4809 1, 96 ; 0, 4809 1, 96 )
131 131
(39, 53%; 56, 65%).
−−
−+
=
Printed with FinePrint trial version - purchase at www.fineprint.com

Xác suất thống kê – Đề tham khảo 2 Trần Ngọc Hội
5
Nói cách khác, với độ tin cậy 99%, tỉ lệ sản phẩm loại A nằm trong khoảng từ 39,53%
đến 56,65%.
Khi trong kho có 1000 sản phẩm loại A, N là tổng số sản phẩm có trong kho, ta có
tỉ lệ sản phẩm loại A là 1000/N. Theo kết quả trên, với độ tin cậy 95%, tỉ lệ sản phẩm
loại A nằm trong khoảng từ 39,53% đến 56,65%, do đó
1000 1000 1000
39,53% 56,65% N
N 56,65% 39,53%
1765, 23 N 2529,72
1766 N 2529
≤≤ ⇔ ≤≤
⇔≤≤
⇔≤≤
Vậy với độ tin cậy 95%, ta ước lượng trong kho có từ 1766 đến 2529 sản phẩm.
Câu 4. Từ giả thiết ta suy ra:
• Cỡ mẫu n = 500.
• Số sản phẩm loại tốt có trong mẫu là m = 275.
• Tỉ lệ mẫu sản phẩm tốt là Fn = m/n = 275/500 = 0,55.
a) Với mức ý nghĩa 1%, tỉ lệ sản phẩm tốt do máy sản xuất có bị thay đổi không?
Ta đưa về bài toán kiểm định giả thiết về tỉ lệ p các sản phẩm tốt với mức ý nghĩa
α = 1% = 0,01:
H0: p = 60% = 0,6 với giả thiết đối H1: p ≠ 0,6.
Ta kiểm định như sau:
Bước 1: Ta có
n0
00
(F p ) n (0, 55 0, 6) 500
z 2, 2822.
p(1 p) 0,6(1 0,6)
−−
== =−
−−
Bước 2: Tra bảng giá trị hàm Laplace để tìm zα thoả
ϕ(zα) = (1 − α)/2 = 0,99/2 = 0,495
ta được zα = 2,58.
Bước 3: Vì |z|= 2,2822 < 2,58 = zα nên ta chấp nhận giả thiết H0: p = 0,6.
Kết luận: Với mức ý nghĩa 1%, có thể nói tỉ lệ sản phẩm tốt do máy sản xuất không bị
thay đổi.
b) Với mức ý nghĩa 5%, có thể nói tỉ lệ sản phẩm tốt do máy sản xuất bị sụt giảm
đi hay không?
Ta đưa về bài toán kiểm định giả thiết về tỉ lệ p các sản phẩm tốt với mức ý nghĩa
α = 5% = 0,05:
H0: p = 60% = 0,6 với giả thiết đối H1: p < 0,6.
Ta kiểm định như sau:
Bước 1: Tương tự câu a), ta có
Xác suất thống kê – Đề tham khảo 2 Trần Ngọc Hội
6
n0
00
(F p ) n
z2,2822.
p(1 p)
−
==−
−
Bước 2: Tra bảng giá trị hàm Laplace để tìm z2α thoả
ϕ(z2α) = (1 − 2α)/2 = 0,90/2 = 0,45
ta được z2α = 1,65.
Bước 3: Vì −z = 2,2822 > 1,65= z2α nên ta bác bỏ giả thiết H0: p = 0,6, nghĩa là
chấp nhận H1: p < 0,6.
Kết luận: Với mức ý nghĩa 5%, có thể nói tỉ lệ sản phẩm tốt do máy sản xuất bị sụt
giảm.
------------------------
Printed with FinePrint trial version - purchase at www.fineprint.com


























