Hong Duc Univers ity
307 Le Lai Str. Thanh Hoa City, Thanh hoa, Viet nam
C¬ häc lîng tö
NguyÔn V¨n
Khiªm
Hong Duc Univers ity
307 Le Lai Str. Thanh Hoa City, Thanh hoa, Viet nam
Bµi 9
Rµo thÕ vµ hè thÕ
Hong Duc Univers ity
307 Le Lai Str. Thanh Hoa City, Thanh hoa, Viet nam
Ta xÐt tiÕp hai vÝ dô ®iÓn h×nh cña chuyÓn ®éng mét chiÒu:
chuyÓn ®éng trong rµo thÕ vµ hè thÕ.
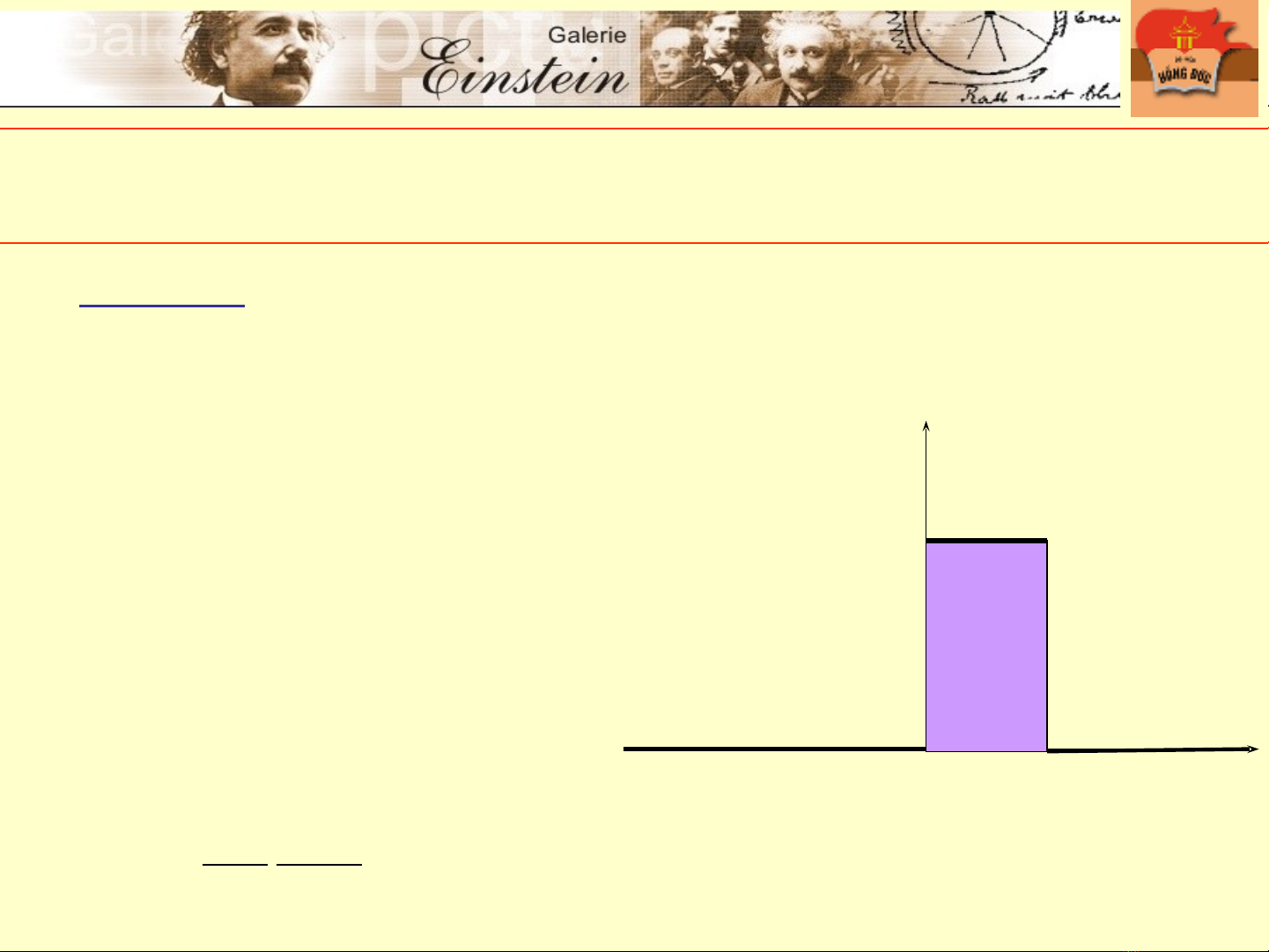
1.Rµo thÕ
Rµo thÕ lµ trêng thÕ cã d¹ng:
<<
><
=
axU
axx
xU 0
00
0
nÕu
hoÆc nÕu,
)(
U
U0
x
0
H×nh 2: BiÓu diÔn Rµo
thÕ
a
gi¸ trÞ cña U(x) t¹i x = 0
vµ x = a cã thÓ cho tuú
ý). §å thÞ hµm U(x) cho
bëi h×nh 2.
ë hai vïng x < 0 vµ x > a,
ph¬ng tr×nh (8.7) trë
thµnh:
ϕ
ϕ
E
dx
d
m
=−
2
22
2
Hong Duc Univers ity
307 Le Lai Str. Thanh Hoa City, Thanh hoa, Viet nam
h
ay
2
2 2
2 (9.1)
d mE
dx
ϕϕ
= − h
NghiÖm tæng qu¸t cña (9.1) cã
d¹ng:
ikxikx
BeAe
−
+=
ϕ
trong ®ã
mEk 2
1
=
Tuy nhiªn, do yªu cÇu tù nhiªn vÒ tÝnh liªn tôc khi “khíp” nghiÖm ë
hai bªn víi nghiÖm khong gi÷a nªn nãi chung c¸c hÖ sè A vµ B
trong (9.2) phi ®îc chän kh¸c nhau cho khong x < 0 vµ khong x >
Do ®ã, nghiÖm cho khong bªn tr¸i sÏ lµ:
ikxikx
L
eBeA
−
+=
11
ϕ
Hong Duc Univers ity
307 Le Lai Str. Thanh Hoa City, Thanh hoa, Viet nam
vµ cho khong bªn phi lµ:
ikxikx
R
eBeA
−
+=
22
ϕ
ë khong gi÷a, ph¬ng tr×nh (9.7) trë thµnh:
ϕϕ
ϕ
EU
dx
d
m
=+−
0
22
2
hay
( )
ϕ
ϕ
2
0
2
2
EUm
dx
d−
−=
NghiÖm tæng qu¸t cña ph¬ng trinh nµy
lµ:
ilxilx
M
eBeA
−
+=
33
ϕ
trong ®ã
( )
0
2UEm
l
−
=
.