intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Giải tích hàm nhiều biến – Chương 2: Tích phân bội

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:166

Thêm vào BST
Báo xấu
63
lượt xem 6
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng "Giải tích hàm nhiều biến - Chương 2: Tích phân bội" cung cấp cho người học các kiến thức: Một số mặt bậc hai thường gặp, tích phân kép, tích phân bội ba. Mời các bạn cùng tham khảo nội dung chi tiết.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Giải tích hàm nhiều biến – Chương 2: Tích phân bội

  1. CHƯƠNG II: TÍCH PHÂN BỘI §0: MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP §1: TÍCH PHÂN KÉP I. Định nghĩa và Cách tính II. Đổi biến trong tích phân kép III. Ứng dụng hình học của tích phân kép §2: TÍCH PHÂN BỘI BA I. Định nghĩa và Cách tính II. Đổi biến trong tích phân bội ba III. Ứng dụng hình học của tích phân bội ba CuuDuongThanCong.com https://fb.com/tailieudientucntt
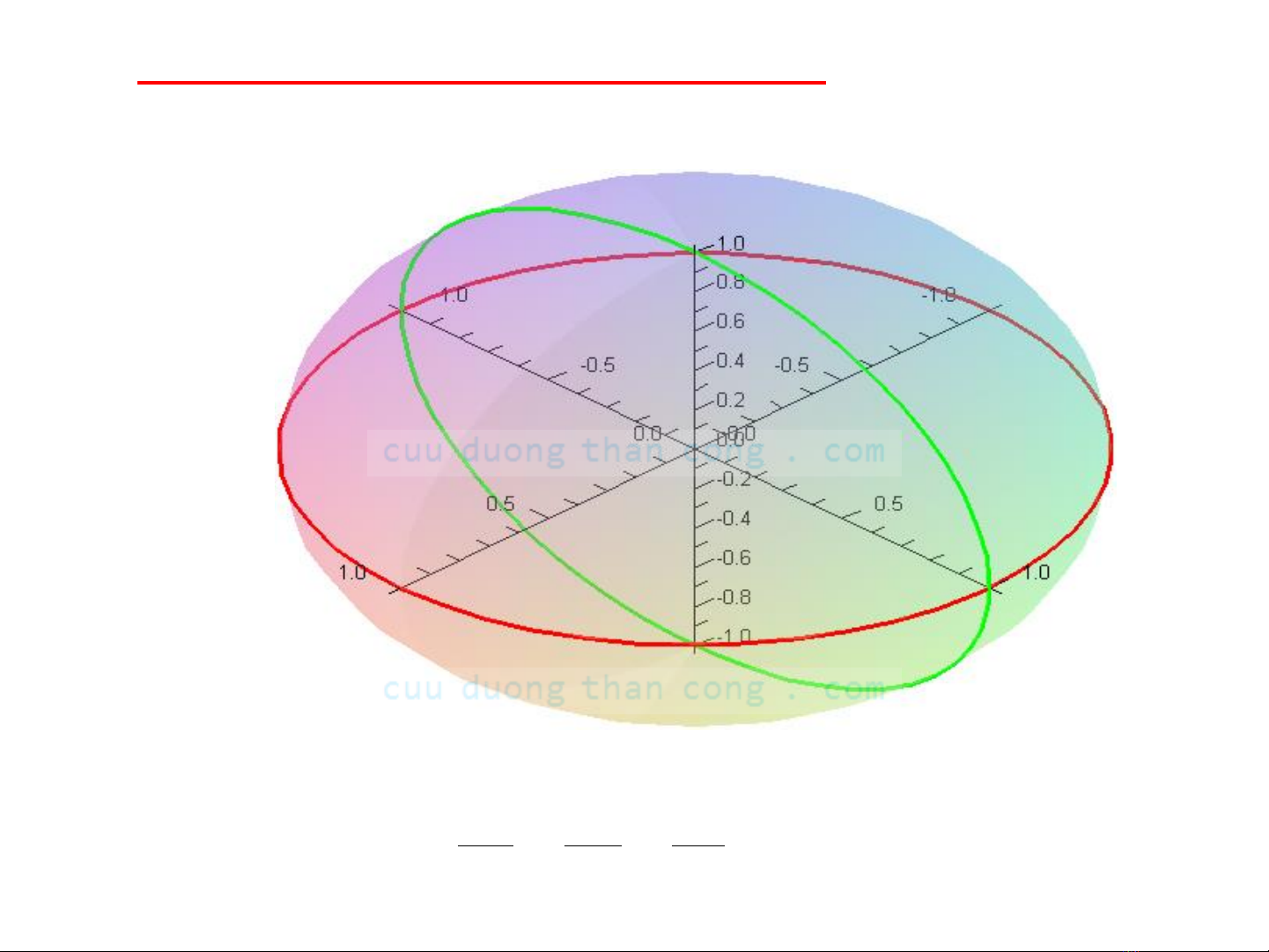
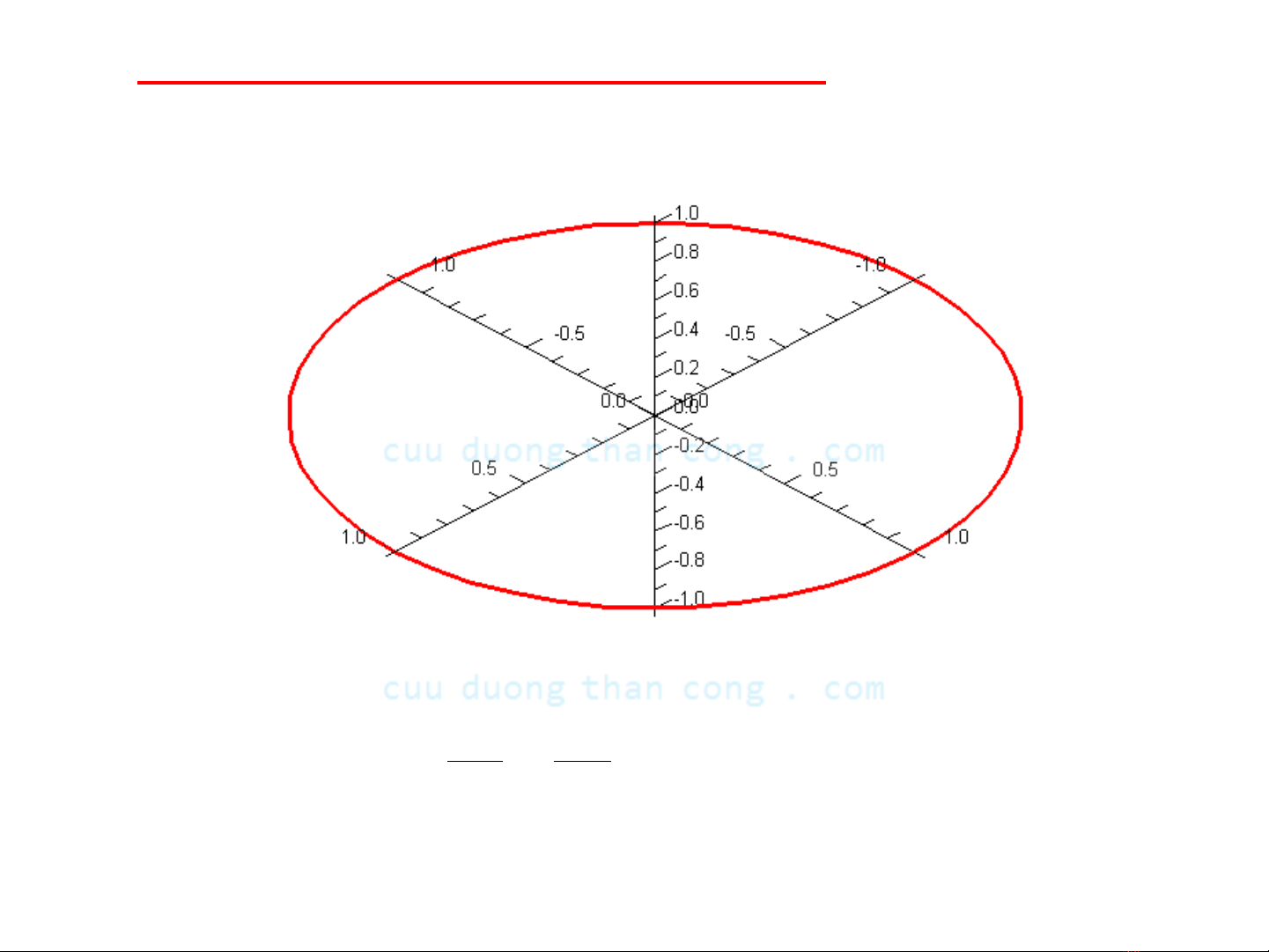
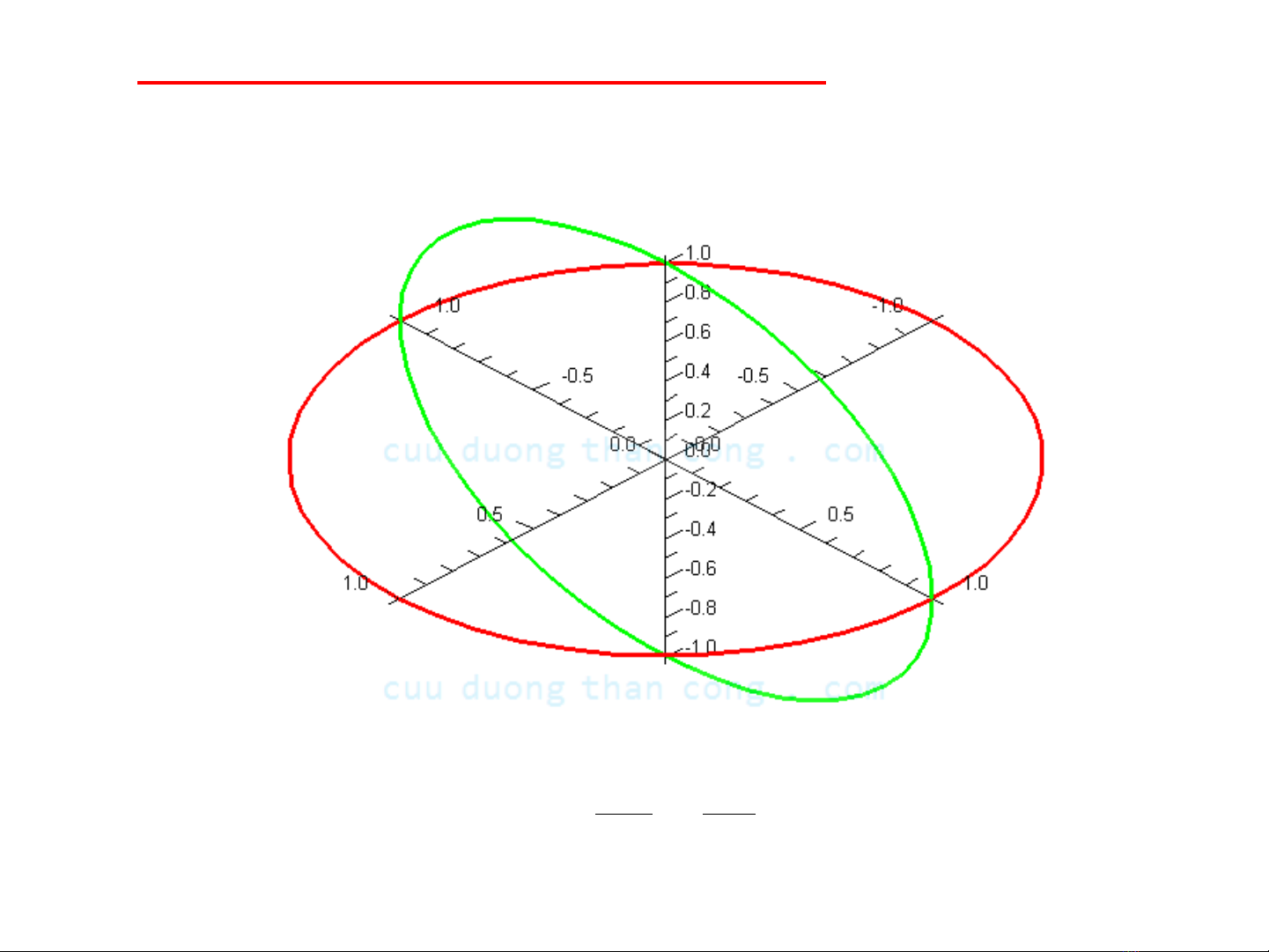
  2. §0. Một số mặt bậc hai thường gặp I. Mặt Ellipsoid: x 2 y 2 z2 1. Phương trình: 2  2  2 1 a b c 2. Cách gọi tên mặt: Với phương trình trên, ta cho x = 0, y = 0, z = 0 ta đều nhận được giao tuyến của mặt với 3 mặt tọa độ làcác đường Ellipse. Tức là nếu cả 3 giao tuyến của mặt S với 3 mặt tọa độ hoặc các mặt song song với các mặt tọa độ đều là ellipse thì ta sẽ gọi mặt S là mặt Ellipsoid 3. Cách vẽ hình Vẽ 3 giao tuyến của S với 3 mặt tọa độ CuuDuongThanCong.com https://fb.com/tailieudientucntt
  3. §0. Một số mặt bậc hai thường gặp x2 y2 Vẽ đường 2  2  1 trên mặt phẳng nằm ellipse a b ngang z = 0 CuuDuongThanCong.com https://fb.com/tailieudientucntt
  4. §0. Một số mặt bậc hai thường gặp y2 z2 trên mặt phẳng Vẽ thêm đường ellipse   1 b2 c2 x=0 CuuDuongThanCong.com https://fb.com/tailieudientucntt
  5. §0. Một số mặt bậc hai thường gặp 2 2 2 Vẽ mặt ellipsoid x y z  2  2 1 2 a b CuuDuongThanCong.com c https://fb.com/tailieudientucntt
  6. §0. Một số mặt bậc hai thường gặp x2+z2=1, y=0 y2+z2=1,x=0 x2+y2=1,z=0 x2 z2 Có thể vẽ thêm đường ellipse 2  2 1 a c trên mặt phẳng y = 0 CuuDuongThanCong.com https://fb.com/tailieudientucntt
  7. §0. Một số mặt bậc hai thường gặp II. Mặt Paraboloid Elliptic: x2 y2 1. Phương trình : z a2 b2 2. Cách gọi tên mặt: Với phương trình trên, ta cho x = 0, y = 0 thì được 2 giao tuyến với 2 mặt tọa độ là 2 đường Parabol và cho z=c, c>0 ta được đường còn lại là 1 đường Ellipse. Tức là nếu 2 trong 3 giao tuyến với các mặt tọa độ hoặc các mặt song song với các mặt tọa độ là 2 Parabol, giao tuyến còn lại là 1 Ellipse thì ta gọi mặt S là Paraboloid Elliptic 3. Vẽ hình CuuDuongThanCong.com https://fb.com/tailieudientucntt
  8. §0. MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP Vẽ đường parabol y2 = z trên mặt phẳng x = 0 CuuDuongThanCong.com https://fb.com/tailieudientucntt
  9. §0. MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP Vẽ đường ellipse x2+y2 = 1 trên mặt phẳng z = 1 CuuDuongThanCong.com https://fb.com/tailieudientucntt
  10. §0. MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP Vẽ mặt parabolid x2+y2 = z CuuDuongThanCong.com https://fb.com/tailieudientucntt
  11. §0. MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP z=x2, y=0 x2+y2=1,z=1 z=y2, x=0 Vẽ thêm đường parabol x2 = z trên mặt phẳng y = 0 CuuDuongThanCong.com https://fb.com/tailieudientucntt
  12. §0. MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP III. Mặt Trụ bậc 2: Định nghĩa mặt trụ bậc 2: Mặt trụ bậc 2 là mặt tạo bởi các đường thẳng song song với 1 phương cố định và tựa lên 1 đường cong cố định. Các đường thẳng đó gọi là các đường sinh của mặt trụ, đường cong cố định gọi là đường chuẩn của mặt trụ. CuuDuongThanCong.com https://fb.com/tailieudientucntt
  13. §0. MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP Thông thường, ta sẽ chỉ gặp các mặt trụ có đường sinh song song với 1 trong 3 trục tọa độ. Mặt trụ song song với trục nào thì phương trình mặt sẽ thiếu biến đó, còn phương trình chứa 2 biến còn lại là phương trình đường chuẩn của mặt trụ trong mặt tọa độ tương ứng và ta gọi tên mặt trụ theo tên của đường chuẩn CuuDuongThanCong.com https://fb.com/tailieudientucntt
  14. §0. MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP Ví dụ: Mặt x2+y2 = 1 Phương trình không chứa z nên nó biểu diễn mặt trụ đường sinh song song với trục Oz, đường chuẩn là đường tròn x2+y2=1 trong mặt phẳng z = 0 và ta gọi đây là mặt trụ tròn xoay theo tên của đường chuẩn Vẽ đường tròn x2+y2=1, trên mặt z=0 Mặt trụ tạo bởi các đường thẳng song song với Oz và tựa lên đường tròn trên CuuDuongThanCong.com https://fb.com/tailieudientucntt
  15. §0. MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP Ví dụ : Mặt z=x2 Phương trình không chứa y nên nó biểu diễn mặt trụ song song với trục Oy, đường chuẩn là parabol z=x2 trên mặt phẳng y=0 nên ta gọi đây là mặt trụ parabol Vẽ parabol z=x2 trong mặt phẳng y=0 Vẽ mặt trụ có đường sinh song song với trục Oy, tựa lên đường chuẩn là parabol z=x2 ở trên CuuDuongThanCong.com https://fb.com/tailieudientucntt
  16. §0. MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP IV. Mặt nón bậc 2 : Mặt nón bậc 2 là mặt tạo bởi các đường thẳng đi qua 1 điểm cố định và tựa lên 1 đường cong cố định. Các đường thẳng đó gọi là các đường sinh của mặt nón, đường cong cố định gọi là đường chuẩn của mặt nón và điểm cố định gọi là đỉnh của nón Ví dụ: Mặt nón x2+y2=z2 Cắt dọc mặt nón bởi các mặt x=0 hoặc y=0 ta được 2 đường thẳng cùng đi qua gốc tọa độ O, cắt ngang bởi mặt z = c và z = -c , c tùy ý, ta được giao tuyến là 2 đường tròn tâm tại (0,0,c) và (0,0,-c) bán kính bằng c CuuDuongThanCong.com https://fb.com/tailieudientucntt
  17. §0. MỘT SỐ MẶT BẬC HAI THƯỜNG GẶP Vẽ giao tuyến x2+y2=1, z=1 Và giao tuyến x2=z2, y=0 Vẽ mặt nón x2+y2=z2, lấy phần z > 0 CuuDuongThanCong.com https://fb.com/tailieudientucntt
  18. §1: Tích phân kép – Định nghĩa và cách tính Dij Thể tích các hình hộp nhỏ với đáy dưới là Dij, trên là phần mặt z=f(x,y) sẽ được tính xấp xỉ với hình hộp chữ nhật đáy là Dij, chiều cao là f(xi,yj). CuuDuongThanCong.com https://fb.com/tailieudientucntt
  19. §1: Tích phân kép – Định nghĩa và cách tính Khi đó, vật thể ban đầu có thể tích xấp xỉ với tổng thể tích các hình hộp chữ nhật nhỏ xếp liên tiếp nhau CuuDuongThanCong.com https://fb.com/tailieudientucntt
  20. §1: Tích phân kép – Định nghĩa và cách tính Định nghĩa tích phân kép : Cho hàm f(x,y) xác định trong miền đóng, bị chặn D Chia miền D thành n phần không dẫm lên nhau là D1, D2, D3, …(các phần không có phần chung) tương ứng có diện tích là ΔS1, ΔS2, ΔS3, … Trên mỗi miền Dk ta lấy 1 điểm Mk(xk,yk) tùy ý. Lập tổng (gọi là tổng tích phân kép của hàm f(x,y)) n Sn   f ( xk , y k )Sk k 1 Hiển nhiên tổng trên phụ thuộc vào cách chia miền D và cách lấy điểm Mk CuuDuongThanCong.com https://fb.com/tailieudientucntt
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright © 2022-2032 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
3=>0