Đ ÔN 1Ề
I. PH N CHUNG Ầ
Câu 1 Cho hàm s : ố
2 3
2
x
yx
+
=−
có đ th ( ồ ị
C
).
a.Kh o sát và v đ th ( C ) . ả ẽ ồ ị
b.Xác đ nh m đ đ ng th ng (d): ị ể ườ ẳ
y x m= +
c t đ th (C) t i hai đi m phân bi t A, B sao cho tamắ ồ ị ạ ể ệ
giác OAB có di n tích b ng ệ ằ
2 3
(v i O là g c t a đ ).ớ ố ọ ộ
Câu 2 a.Gi i h ph ng trình: ả ệ ươ
2
4 2 2
1
log log 16 4 log 2
4 8 16 4
xy
y
x
x x xy x x y
+ = −
+ + = +
b.Gi i ph ng trình: ả ươ
2
3
1 2 os 2 tan 2 cot 4 3
sinx.cos
c x x x
x
−+ + =
.
Câu 3 a.Tính tích phân sau:
3
2 3 sinx-cosx
dx
I
π
π
=+
∫
b.Tìm m đ ph ng trình sau có nghi m: ể ươ ệ
1 6 8 1 6 8 6
x m
x x x x +
+ + − + + − − =
Câu 4 a.Cho hình chóp tam giác S.ABC, trong đó
, SC = a và ABC là tam giác vuông cân đ nhỉ
C, gi s góc gi a hai m t ph ng (SCB) và (ABC) b ng ả ử ữ ặ ẳ ằ
α
. Tính th tích kh i chóp S.ABC theo a và ể ố
α
.
Tìm
α
đ th tích đó đ t giá tr l n nh t.ể ể ạ ị ớ ấ
b.Trong m t ph ng t a đ Oxy, cho đ ng tròn (C): ặ ẳ ọ ộ ườ
( ) ( )
2 2
1 2 9x y− + − =
. L p ph ng trình đ ng th ngậ ươ ườ ẳ
(d) đi qua g c t a đ và c t (C) t i hai đi m A, B sao cho AB = 4.ố ọ ộ ắ ạ ể
Câu 5 .Xét các s th c d ng x, y, z th a mãn: ố ự ươ ỏ
1x y z+ + =
. Tim giá tr nh nh t c a bi u th c: ị ỏ ấ ủ ể ứ
( ) ( ) ( )
2 2 2
x y z y z x z x y
Pyz zx xy
+ + +
= + +
II. PH N T CH NẦ Ự Ọ
1.Theo ch ng trình chu n.ươ ẩ
Câu VI a.
1/ Trong m t ph ng v i h t a đ Oxy, cho đi m I(1 ; 2) và hai đ ng th ng dặ ẳ ớ ệ ọ ộ ể ườ ẳ 1: x – y = 0,
d2: x + y = 0. Tìm các đi m A trên Ox, B trên dể1 và C trên d2 sao cho tam giác ABC vuông cân t i A đ ngạ ồ
th i B và C đ i x ng v i nhau qua đi m I.ờ ố ứ ớ ể
2/ Trong không gian v i h t a đ Oxyz, cho đ ng th ng d: ớ ệ ọ ộ ườ ẳ
2
1
1
1
2
+
=
−
=zyx
và hai m t ph ngặ ẳ
022:)(,052:)( =++−=+−+ zyxzyx
βα
. L p ph ng trình m t c u (S) có tâm trên d và ti p xúc v iậ ươ ặ ầ ế ớ
hai m t ph ng đã cho.ặ ẳ
Câu VI a. Gi i ph ng trình sau trong t p s ph c: ả ươ ậ ố ứ
010)45()22(
23
=−−+−+ iziziz
2. Theo ch ng trình nâng caoươ .
Câu VI b.
1/ Trong m t ph ng v i h t a đ Oxy, cho đ ng th ng d: x – y – 3 = 0 và đi m M( 2cosặ ẳ ớ ệ ọ ộ ườ ẳ ể 2t ; 2(1 +
sint.cost) ( t là tham s ). Ch ng minh r ng t p h p c a đi m M là đ ng tròn (C). Hãy vi t ph ng trìnhố ứ ằ ậ ợ ủ ể ườ ế ươ
đ ng tròn (C’) đ i x ng v i (C) qua d.ườ ố ứ ớ
2/ Trong không gian v i h t a đ Oxyz, cho hai đ ng th ng dớ ệ ọ ộ ườ ẳ 1:
=
=
−=
tz
y
tx
3
22
d2:
21
1
1
2zyx =
−
=
−
. Vi t ph ng trình đ ng th ng d song song v i Oz c t c dế ươ ườ ẳ ớ ắ ả 1 và d2.
Câu VII b. (1 đi m).Gi i h ph ng trình : ể ả ệ ươ
=+−+
=−
1)(log)(log
2
32
22
yxyx
yx
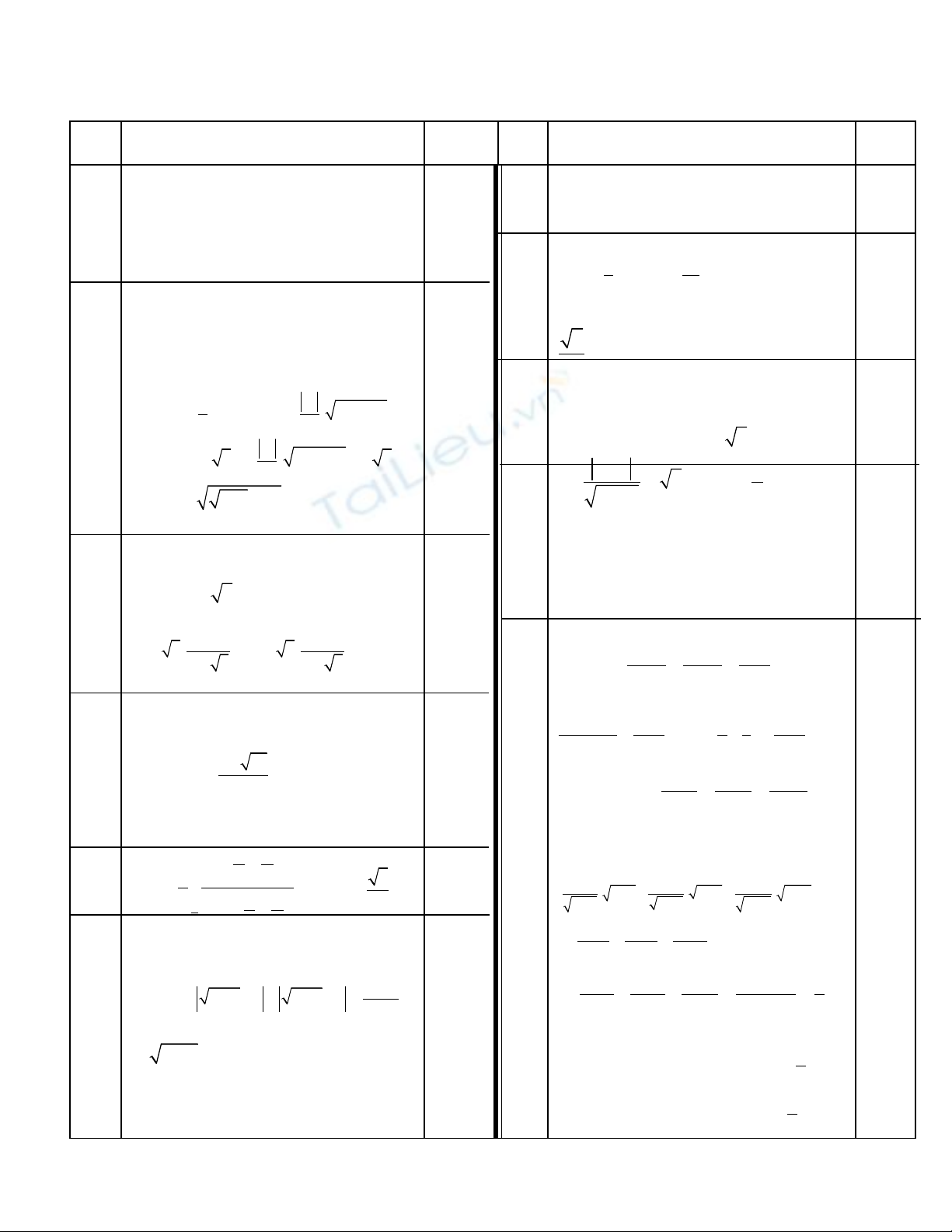
ĐÁP ÁN Đ THI TH ĐH L N MÔN TOÁN L P 12 NĂM H C 2008-2009Ề Ử Ầ Ớ Ọ
Câu H ng d nướ ẫ Đi mểCâu H ng d nướ ẫ Điể
m
Câu
1a
Câu
1b
Câu
2a
Câu
2b
Câu
3a
Câu
3b
+) TXĐ: D = R
+) Tính đ c y’, KL kho ng đ nượ ả ơ
đi u, đi m c c tr , ti m c nệ ể ự ị ệ ậ
+) BBT:
+) Đ th :ồ ị
+) PT hoành đ giao đi m:ộ ể
2
( 4) 2 3 0x m x m+ − − − =
(*) có hai
nghi m PT ệ
⇔
2
28 0m m R
+ > ⇔ ∈
+) G i A(xọ1; x1+ m), B(x2; x2+ m),
v i xớ1, x2 là các nghi m PT (*).ệ
+)
2
1( ; ). . 28
2 2
OAB
m
S d O d AB m
= = +
+)
2
2 3 . 28 2 3
2
OAB
m
S m
= ⇔ + =
208 14m
⇔ = ± −
+) ĐK:
> > ≠ ≠
0, 0, 1, 1x y xy y
+) T PT (1) ta có: xy = 4ừ
+) Th vào (2) ta có: xế2–4x + 1 = 0
2 3x⇔ = ±
+) KL : H có các nghi m làệ ệ :
4 4
2 3; ; 2 3;
2 3 2 3
+ −
+ −
+) ĐK: sin4x
≠
0
+) PT
3
cot 4 4cot4 3 0x x⇔ − − =
cot4 1
1 13
cot4 2
x
x
=
⇔±
=
+) Gi i đúng các h nghi mả ọ ệ
+) KL: K t lu n đúngế ậ
+)
π
π
π
π
+
=
+
∫
2
3
12 6
8cos 2 6
x
d
Ix
+)
= − 3
4
I
+) ĐK:
≥8x
+) PT
+
⇔ − + + − − =
8 3 8 3 6
x m
x x
+) N u ế
17x≥
, ta có PT tr thànhở :
12 8x x m+ − =
. PT có nghi mệ
17x
≥
⇔
77 100m
≤ ≤
+) N u ế
8 17x≤ <
, ta có PT tr ở
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.25
0.5+0,5
0.25
0.25
0.25
Câu
4a
Câu
4b
Câu
5a
Câu
5b
thành : 36 – x = m. PT có nghi m ệ
⇔
19 28m< ≤
+) KL:
77 100m
≤ ≤
ho c ặ
19 28m
< ≤
+)
V hình đúngẽ
+)
32
1
V= . sin .(1 sin )
3 3
ABC
a
SA S
α α
= −
+) Xét h/s
2
.(1 )y t t
= −
suy ra Vmax =
2
2
khi
0
45
α
=
+) Đ ng tròn I(1; 2), R = 3.ườ
Đường th ng ẳ
( )∆
c n tìm y = kxầ
+) YCBT
⇔
( , ) 5d I ∆ =
2
21
52
1
kk
k
−
⇔ = ⇔ = −
+
+)
(3; 1;2), (1;3; 1)
P d
n u= − = −
uur uur
.
Giao đi m c a (d) và (P) là đi mể ủ ể
A(15; 28; - 9)
+) Đ ng th ng (d’) c n tìm qua Aườ ẳ ầ
nh n ậ
, ( 4;5;10)
P d
n u
= −
uur uur
là VTCP
( '):d⇒
15 28 9
4 5 10
x y z
− − +
= =
−
+) Ta có:
( ) ( )
22 2
1 1 4
+
= + + ≥
+ +
x y z x x
y z
yz y z y z y z
Do đó
2 2 2
4x y z
Py z z x x y
≥ + +
+ + +
+) Aùp d ng BĐT B.C.S ta có:ụ
2
( )x y z+ + =
2
. . .
x y z
y z z x x y
y z z x x y
+ + + + +
+ + +
2 2 2
(2 2 2 )
x y z x y z
y z z x x y
≤ + + + +
+ + +
2 2 2
1
2 2
x y z x y z
y z z x x y
+ +
⇒ + + ≥ =
+ + +
T đó ta có ừ
2P
≥
D u “=” x y ra khi ấ ả
1
3
x y z= = =
KL: minP = 2, khi
1
3
x y z= = =
0.25
0.25
0.25
0.5
0.25
0.75
0.5
0.5
0.25
0.5
0.25
H tế