Trêng THPT NguyÔn §×nh ChiÓu
---------------------------------------------------------------------------------------------------------------------
Tên bài soạn: HAI ĐƯỜNG THẲNG SONG
( 2 tiết : 19+20)
( Hình học 11 )
A. MỤC ĐÍCH YÊU CẦU: Làm cho HS nắm được :
Vị trí tương đối của 2 đt phân biệt: chéo nhau, cắt nhau và song song
Các tính chất của các đt song song và định lí về giao tuyến của 3 mp
Cách chứng minh 2 đt song song
B. CHUẨN BỊ:Đọc kĩ SGK + SGV- Sử dụng mô hình tứ diện, hình chóp
C. TIẾN TRÌNH GIỜ DẠY:
I.Kiểm tra bài cũ:Phát biểu các tính chất thừa nhận của HHKG, cách xác định mp.
AD: làm BT17 (SGK)
II. Bài mới:
TG
Phương pháp Nội dung
H1? Nêu vị trí tương đối
của 2 đt trong mp ?
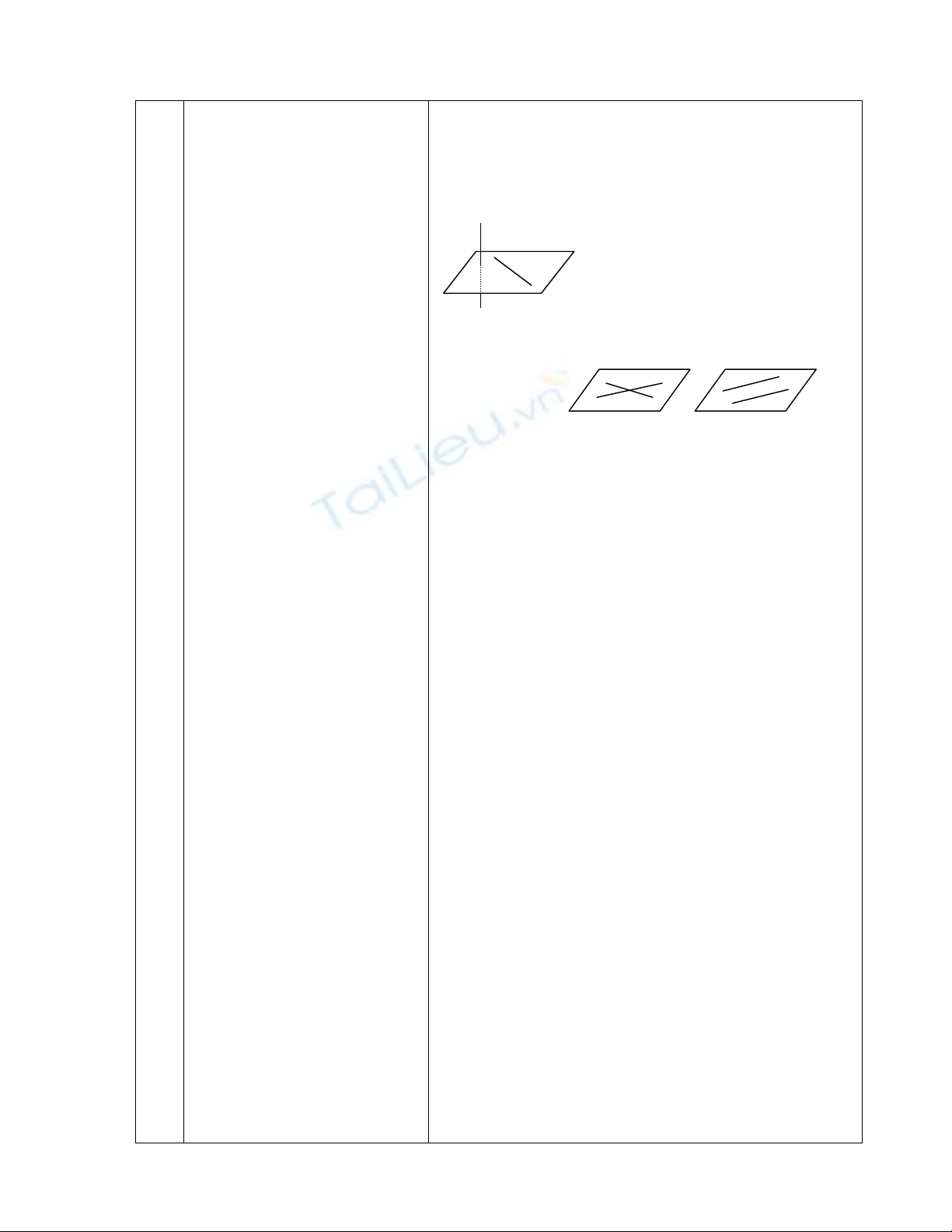
1.Vị trí tương đối giữa 2 đường thẳng phân
biệt:
?1a) a, b không cùng nằm trên 1 mp
b) a, c hoặc b, c cùng nằm trên 1 mp
Trêng THPT NguyÔn §×nh ChiÓu
---------------------------------------------------------------------------------------------------------------------
H2?Nhìn hình 48(SGK)
xét xem a,b có cùng
thuộc mp không ? Có mp
chứa a và c hoặc chứa b
và c không ?
H3? Xét vị trí tương đối
của 2 đường thẳng AB và
CD ?
H4?Cho 2 đt chéo nhau a
và b. Có hay không 2 đt
p, q song song cắt cả 2 đt
a, b ?
H5?Nêu tính chất của 2
đt // trong mp. Chúng có
còn đúng trong không
gian không ?
H6?Cho (P) (R) = a
(Q) (R) = b , (P) (Q)
Suy ra:
-
N
ếu không có mp n
ào ch
ứa cả a, b th
a và b chéo nhau
-Nếu có mp chứa cả a và b thì: a b = a
// b
a b = A a cắt b
ĐN: a chéo b khi a, b không đồng phẳng
a // b khi a, b đồng phẳng và a b =
HĐ1: AB và CD chéo nhau
HĐ2:Không có
2. Hai đường thẳng song song:
Tính chất 1:Cho A a . ! b qua A và // a
Tính chất 2: ba
cb
ca //
//
//
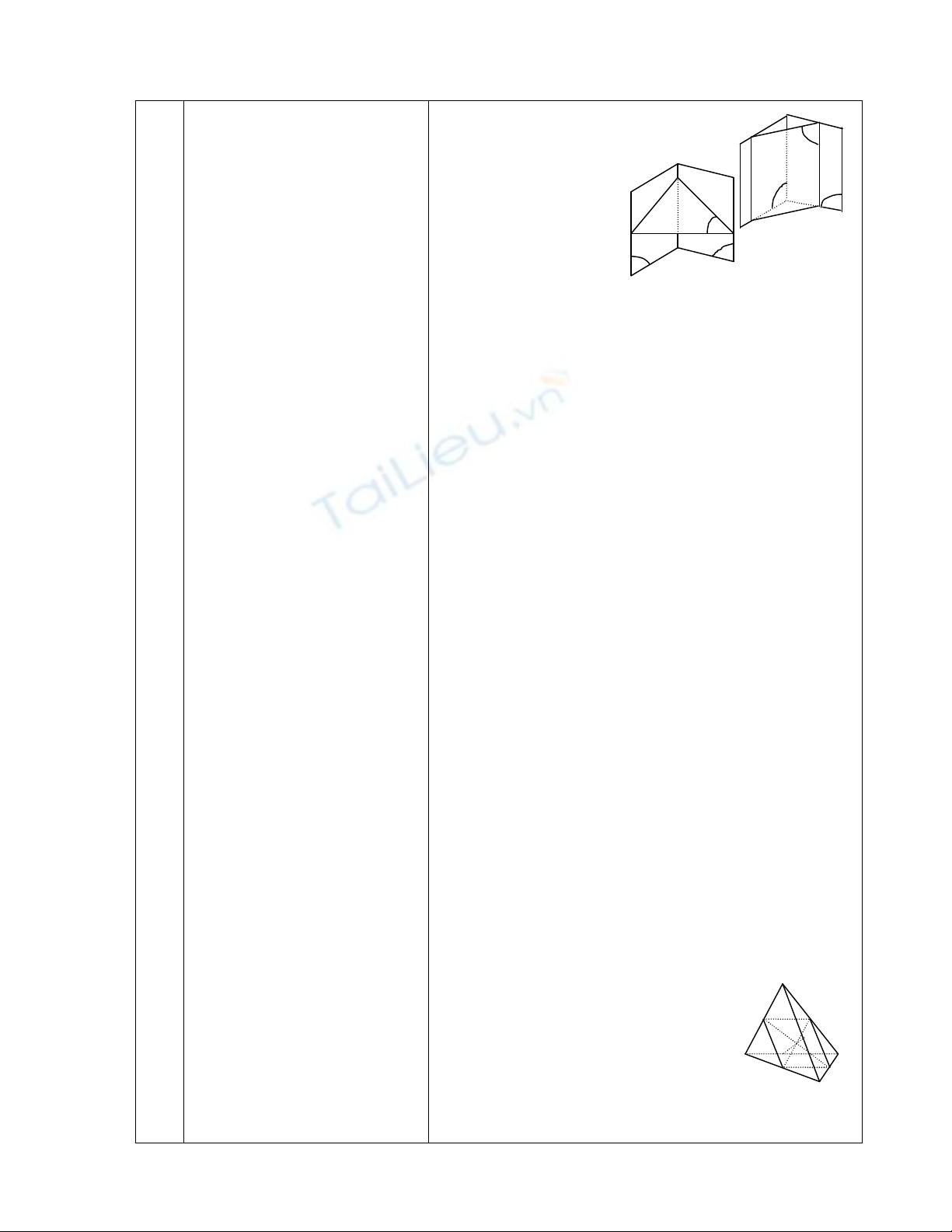
?2 Những vị trí tương đối giữa a và b là cắt
nhau hoặc //
a
b
a
b
I
a
b
Trêng THPT NguyÔn §×nh ChiÓu
---------------------------------------------------------------------------------------------------------------------
= c
Nêu vị trí tương đối của
a, b.
H7? Gọi HS làm HĐ3
H8? Nêu kết quả của
HĐ3 thành định lí.
H9? Dùng định lí chứng
minh hệ quả.
H10?Gọi HS lên làm
HĐ3:Nếu a, b cắt nhau thì giao
tuyến phải nằm trên c.
Vậy a, b, c đồng qui
Nếu a // b thì a, c
không thể cắt nhau,
b,c không thể cắt nhau
và a, c (P), b, c (Q) nên a // c và b // c
Định lí: (P) (R) = a, (Q) (R) = b, (P)
(Q) = c
a, b, c đồng qui hoặc a, b, c song song
Hệ quả:
bu
au
bau
uQP
Qb
Pa
ba ////
)()(
)(
)(
//
HĐ4:Gọi (R) mp(a, b) ,(P) (Q) = u, (R)
(P) = a , (R) (Q) = b. Vì a // b nên a // c, b //
c. c a hoặc c b
khi (P) (Q) = a hoặc (P) (Q) = b
3. Các ví dụ:
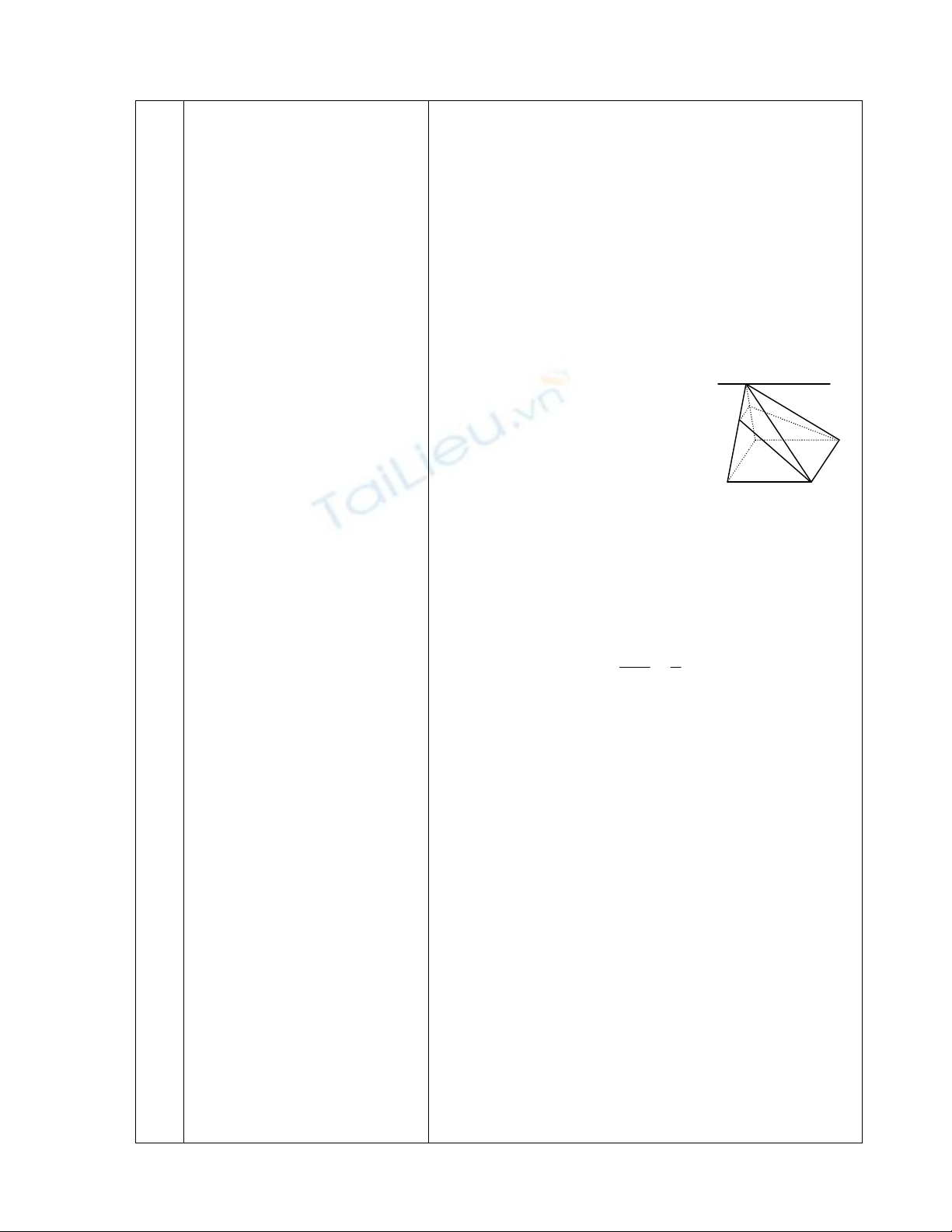
Ví dụ 1:Cho tứ diện ABCD. Gọi M,
P Q
a
b
c
R
P Q
a
b
c
R
A
B
C
D
M
N P
Q
S G R
Trêng THPT NguyÔn §×nh ChiÓu
---------------------------------------------------------------------------------------------------------------------
VD1
H11?Nêu PP tìm giao
tuyến của 2 mp, tìm thiết
diện
H12? Gọi HS đứng tại
chỗ trả lời
H13?Cho HS đứng tại
chỗ trả lời và giải thích .
H14?Hãy chọn 3 mp
phân biệt cắ nhau theo 3
giao tuyến là 3 đt đã cho
N, P, Q, R, S là TĐ của AB, CD,
BC, DA, AC, BD. CMR: MN, PQ,
RS đồng qui tại TĐ G của mỗi đoạn.
G gọi là trọng tâm của tứ diện
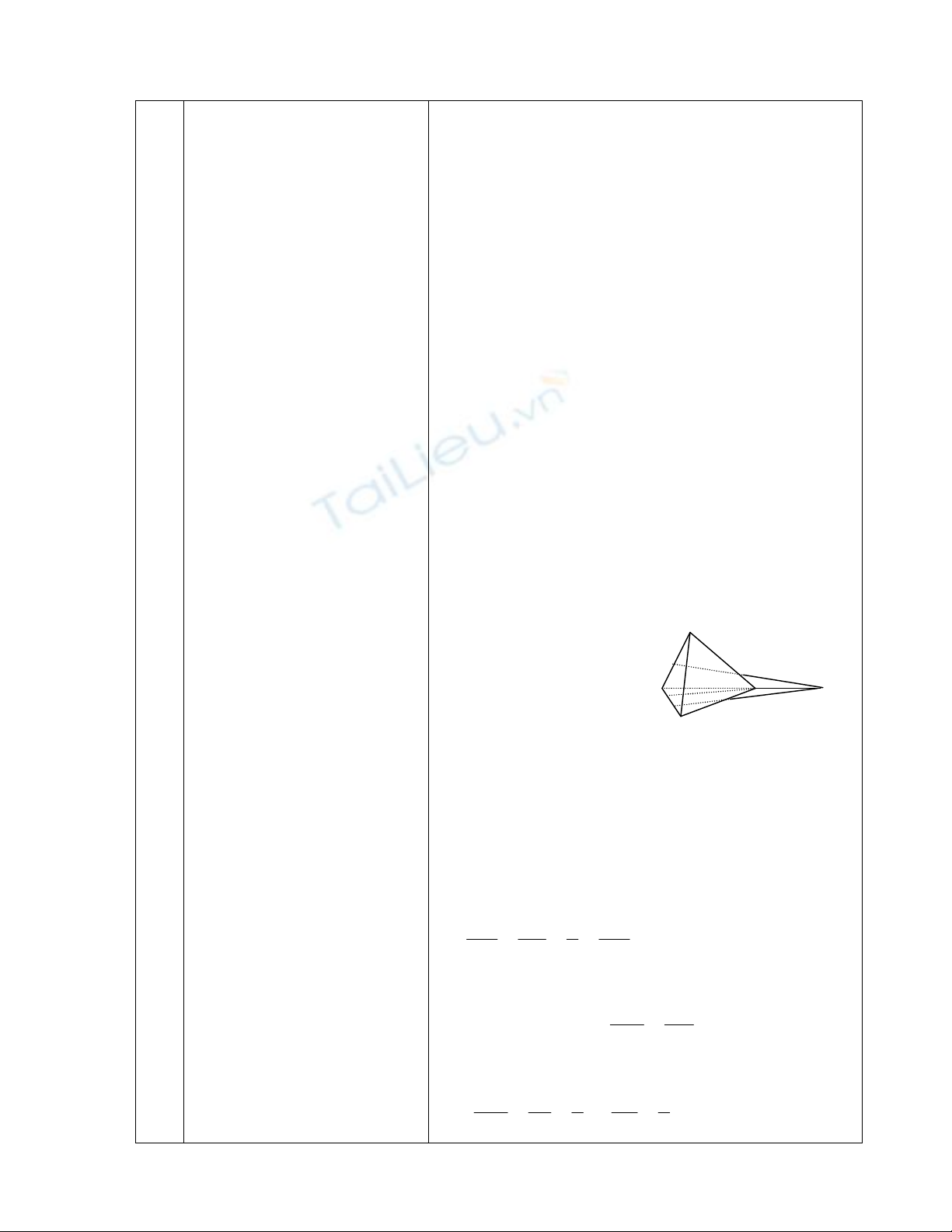
Ví dụ 2:Cho hình chóp SABCD có đáy là hbh
a)Tìm (SAB) (SCD)
b)Xác định thiết diện của
hình chóp với (MBC)
trong đó M là điểm ở
giữa S và A sao cho
3
1
SA
SM
Bài 18: a) Đ b) S c) S d) Đ
Bài 19:MQ, NP và MP, NQ là các đt chéo
nhau
Bài 20:
a)P, Q, R, S đồng phẳng (PQRS) (ABC)
= PQ, (PQRS) (ACD) = RS, (ABC)
(ACD) = AC PQ, RS, AC hoặc đôi một
song song hoặc đồng qui
S
M
N
A
B
C
D
Trêng THPT NguyÔn §×nh ChiÓu
---------------------------------------------------------------------------------------------------------------------
?
H15?Nêu PP tìm giao
điểm của đt và mp ?
H16? Tìm giao điểm S
của AD và (PQR).
H17?CM C là TĐ của AI
H18? Nêu phương pháp
lấy tỉ số của các đoạn
thẳng
b)Tương t
Bài 21:a) PR // AC: Chọn (ACD) chứa AD
(ACD) (PQR) = Qx // PR // AC Qx
AD = S
Mà Qx (PQR) nên S = AD (PQR)
b) PR cắt AC :
Gọi I = PR AC (ACD) (PQR) = QI
QI AD = S mà QI (PQR) nên S = AD
(PQR)
Bài 22:
Gọi I = PR AC
(ACD) (PQR) = IQ
IQ AD = S
Từ C kẻ CC’// AB
AP
CC
RB
RC
PB
CC '
2
1' C là TĐ của AI
Từ C kẻ CC1 // AD. 1
1 QD
QC
SD
CC
Mà 2SDS
2
1
S
2
1
S
1 A
A
SD
IA
IC
A
CC
A
B
C
D I
P
S
Q
E
R