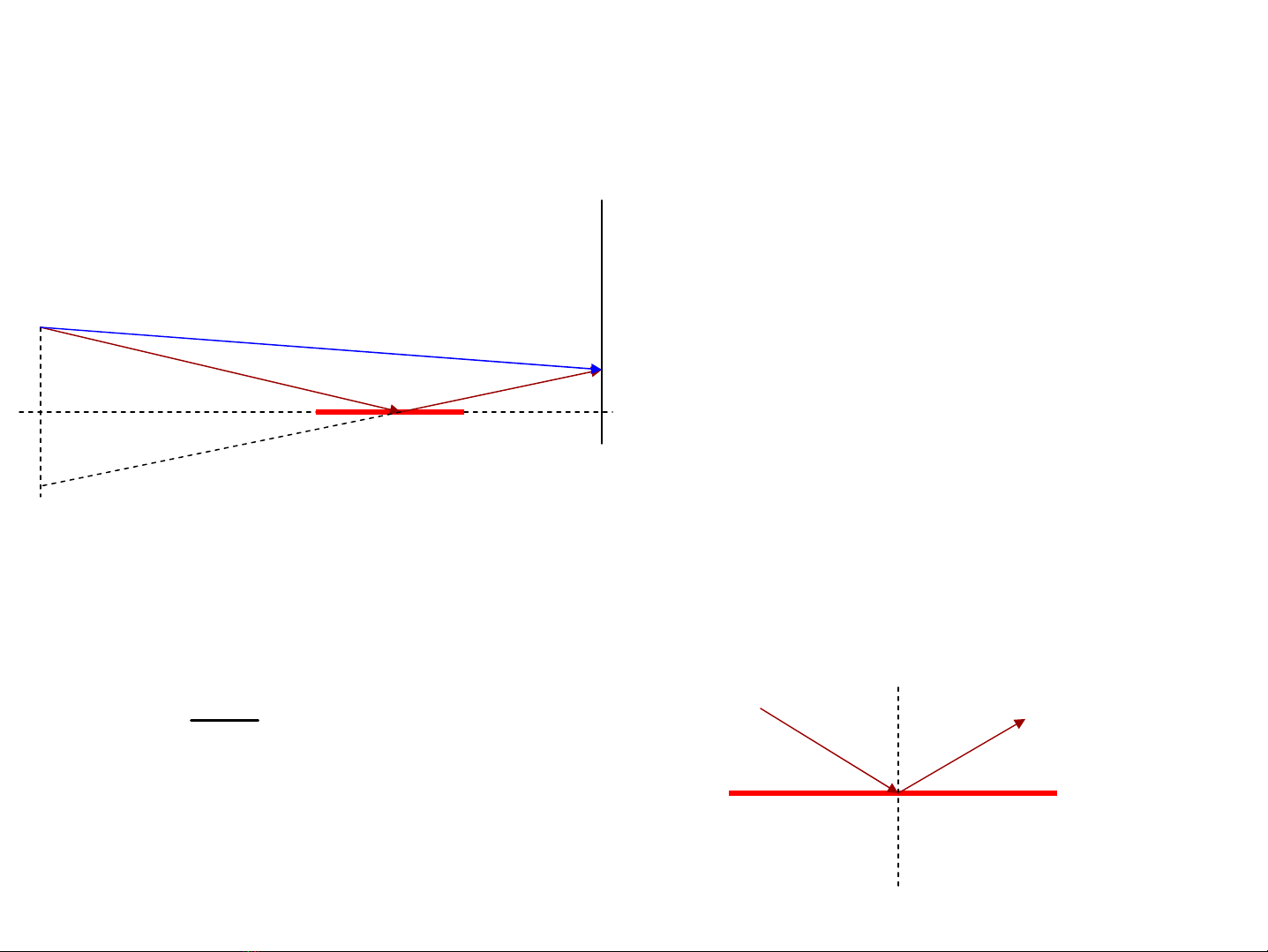
3.3. HiÖn t−îng giao thoa do ph¶n x¹
• ThÝ nghiÖm cña L«i (Lloyd)
O
I
MV©n s¸ng
L1-L2=OI+IM-OM =kλ
V©n tèi
L1-L2=OI+IM-OM=(2k+1)λ/2
Theo lý thuyÕt
Thùc tÕ ng−îc l¹i →Sau ph¶n x¹ ®¶o pha
π+−
λ
π
=ϕΔ )LL(
2
21
L1cña tia ph¶n x¹
dμi thªm λ/2
n1
n2
ChØ khi n2> n1
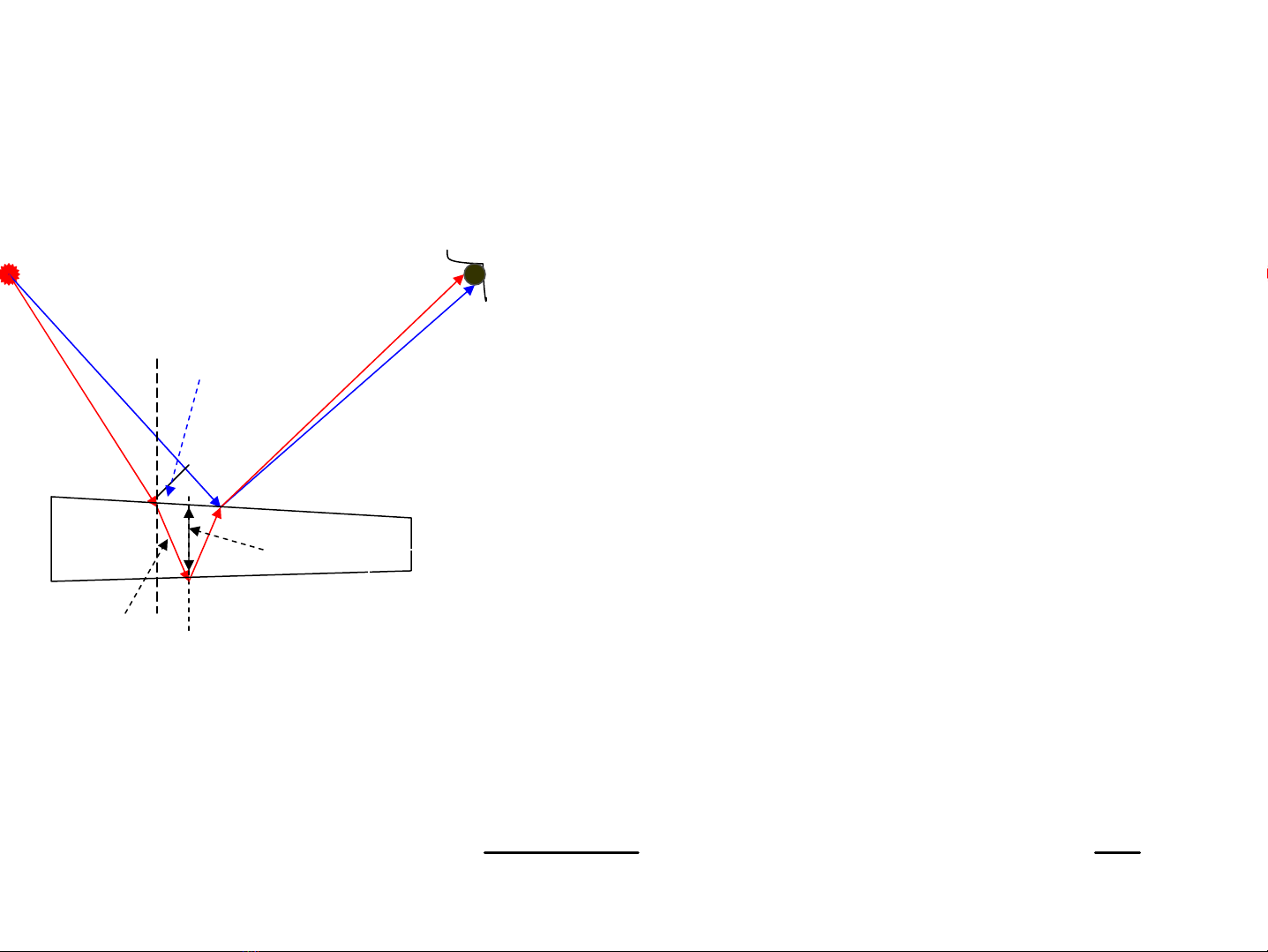
4. Giao thoa g©y bëi c¸c b¶n máng
4.1. B¶n máng cã bÒ dÇy
thay ®æi -V©n cïng ®é dμy
O
C
M
Bd
R
nL1-L2=OB+n(BC+CM)-(OM+λ/2)
= n(BC+CM)-RM-λ/2
HiÖu quang lé:
i1
i2
RM=BM.sini1=2d.tgi2.sini1BC = CM = d/cosi2
2
isintgi.d2
icos
d2
nLLL 12
2
21
λ
−−=−=Δ
Tia lã cña tia ph¶n x¹ tõ ®¸y
d−íi (®á) giao thoa víi tia
ph¶n x¹ tõ mÆt trªn (xanh)
cña tÊm
i1
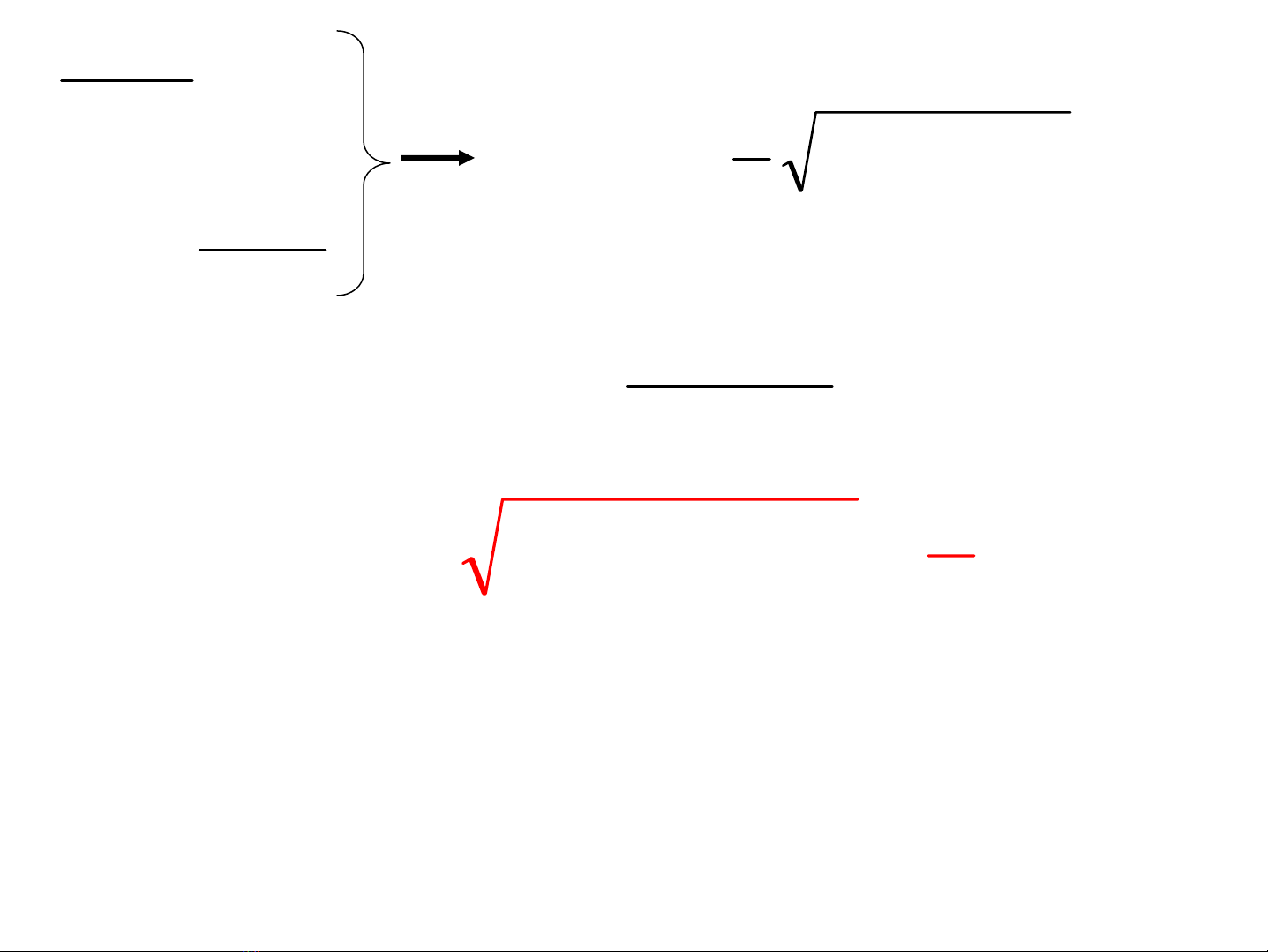
n
isin
isin
2
1=
n
isin
isin 1
2=
1
22
2isinn
n
1
icos −=
)isinn(
icosn
d2
isintgi.d2 1
22
2
12 −=
2
)isinn(d2L 1
22
λ
−−=Δ
V©n s¸ng: L1-L2=kλV©n tèi: L1-L2=(2k+1)λ/2
Gãc nh×n x¸c ®Þnh => i1x¸c ®Þnh
=>Mçi v©n øng víi mét ®é dÇy d x¸c ®Þnh
=> V©ncïng®édÇy
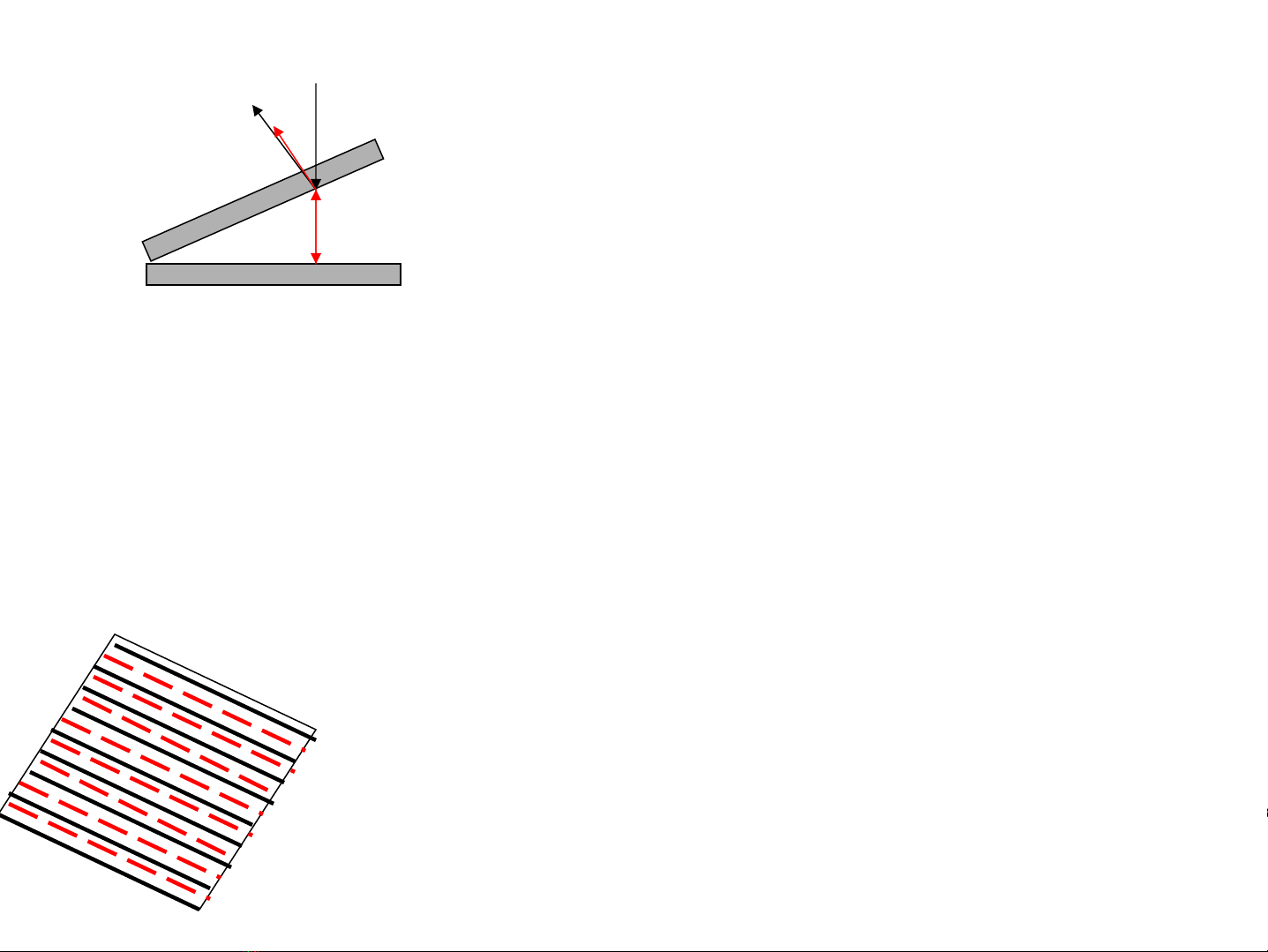
•Nªm kh«ng khÝ
d
HiÖu quang lé L1-L2=2d+ λ/2
V©n s¸ng: L1-L2=2d+ λ/2=k λ
dS= (2k-1)λ/4
V©n tèi: L1-L2=2d+λ/2=(2k+1) λ/2
dT=k.λ/2
øng dông: KiÓm tra ®é ph¼ng
cña kÝnh sai sè 0,03-0,003 μm
Tia lã cña tia ph¶n x¹ tõ ®¸y
d−íi (®en) tÊm trªn giao
thoa víi tia ph¶n x¹ tõ mÆt
trªn (®á) cña tÊm d−íi
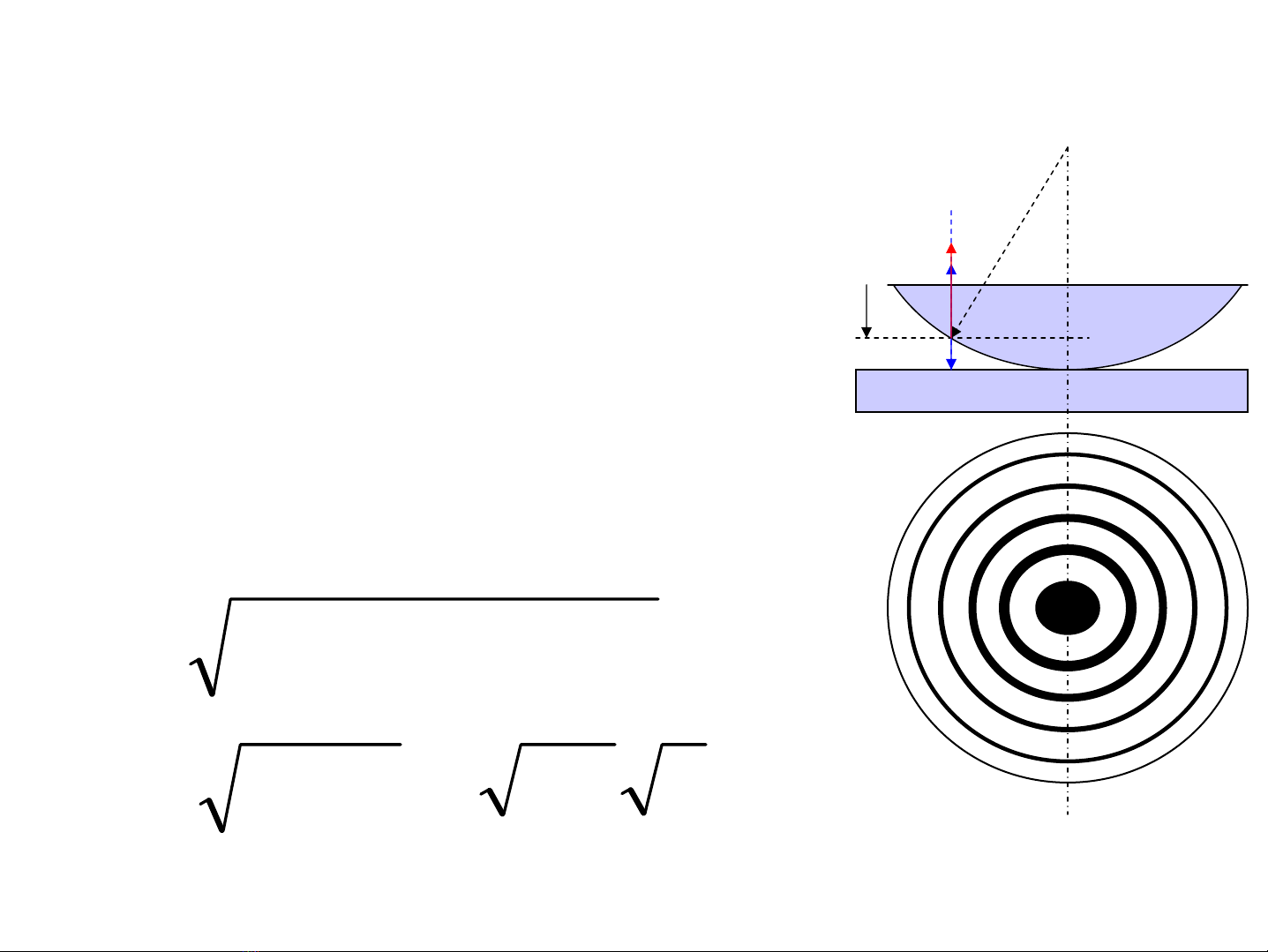
•V©ntrßnNiut¬n
dk
R
rk
V©n tèi : dk=k. λ/2
B¸n kÝnh v©n:
2
k
2
k)dR(Rr −−=
kRRd2r kk λ=≈
V©n s¸ng : dk=(2k-1). λ/4
Tia ph¶n x¹ tõ tÊm ph¼ng
(xanh) vμTia ph¶n x¹ tõ mÆt
cong cÇu (®á) giao thoa víi
nhau:


























