Bài giảng Phương pháp lặp đơn. Giải phương trình f(x)=0

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:15

Thêm vào BST

Báo xấu

39
lượt xem 4
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng "Phương pháp lặp đơn. Giải phương trình f(x)=0" là tài liệu học tập dành cho các em sinh viên, giúp các em nắm được nội dung về phương pháp lặp đơn và ứng dụng vào giải phương trình f(x)=0. Đây cũng là tài liệu tham khảo hữu ích dành cho quý thầy cô giáo trong quá trình biên soạn và chuẩn bị bài giảng. Mời các bạn cùng tham khảo chi tiết tại đây.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Phương pháp lặp đơn. Giải phương trình f(x)=0

PHƯƠNG PHÁP LẶP ĐƠN GIẢI PT f(x)=0
Ý tưởng phương pháp - Đưa về phương trình tương đương f ( x) = 0  x =  ( x) - Lập dãy số xn =  ( xn−1 ) , x0   a, b  - Nếu dãy hội tụ thì giới hạn là nghiệm của phương trình
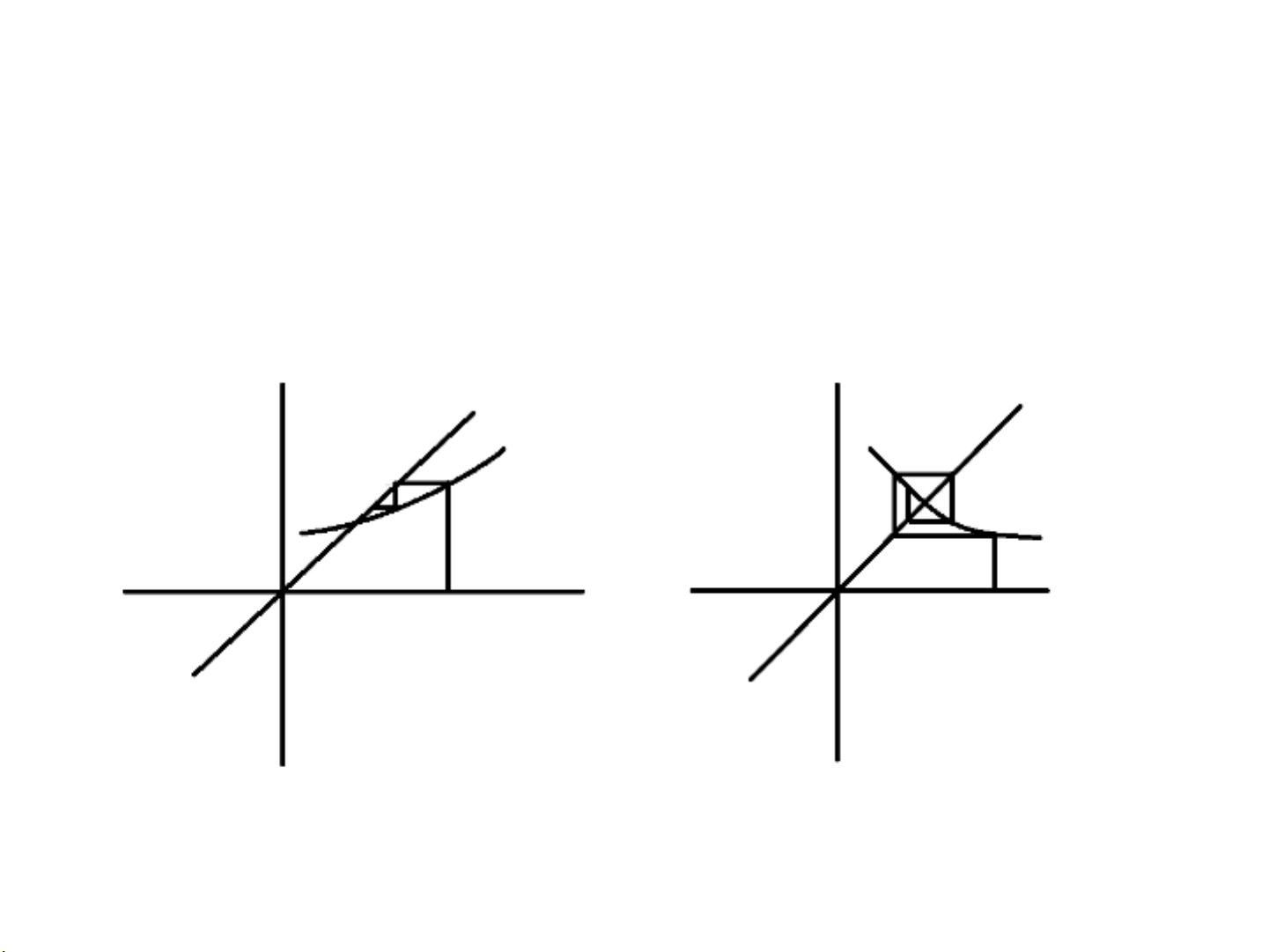
Ý tưởng phương pháp • Trường hợp có xu hướng hội tụ y y  ( x)  ( x) 0 x0 x 0 x0 x
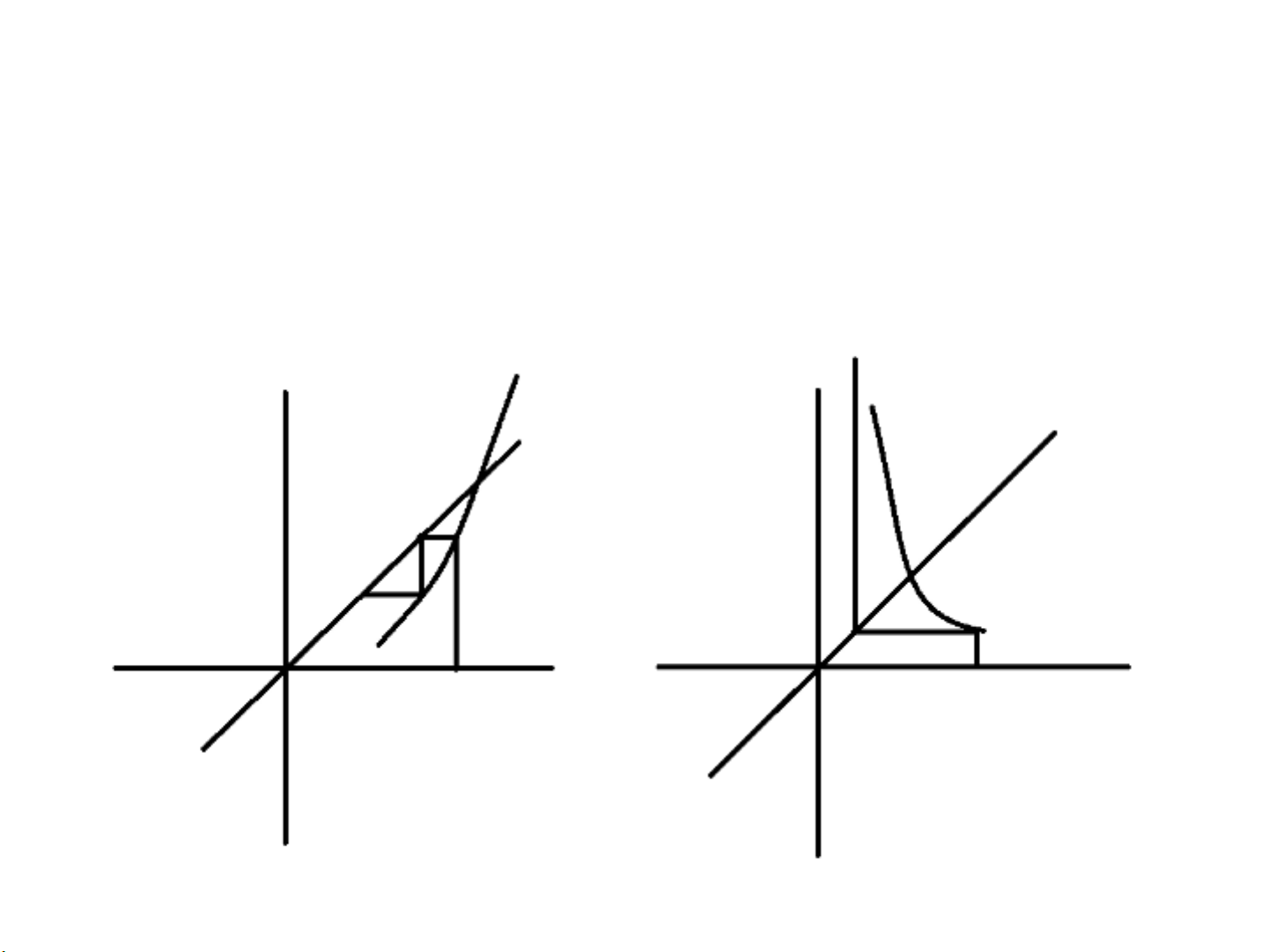
Ý tưởng phương pháp • Trường hợp có xu hướng không hội tụ y y x0 x x0 x
Nội dung phương pháp – Đưa phương trình về dạng x = (x),  gọi là hàm lặp. – Chọn x0  [a, b] làm xấp xỉ đầu – Tính dãy xn theo công thức: xn = (xn – 1), n = 1, 2, 3,... – Nếu dãy xn → , n →  thì phương pháp lặp hội tụ và lấy nghiệm gần đúng x* = xn nào đó.
Điều kiện hội tụ Định lý: Giả sử (a, b) là khoảng phân ly nghiệm (chứa nghiệm đúng ) của phương trình f(x) = 0. Xét phương pháp lặp với hàm lặp : x = (x),  và ' liên tục trên [a, b]. Nếu: 1) Mọi x [a, b], (x)  [a, b],… 2) Với mọi x  [a, b]: |'(x)|  q
Đánh giá sai số • Công thức sai số theo xấp xỉ ban đầu: n q xn −   x1 − x0 1− q • Công thức sai số theo hai xấp xỉ liên tiếp q xn −   xn − xn−1 1− q
Nhận xét • Nếu ’(x) > 0 với mọi x thuộc [a,b], từ xn –  = ’(c)( xn –1 – ) cho thấy dãy {xn} dần đến  từ một phía. Ngược lại, dãy xn dần đến  từ hai phía, giao động xung quanh . • Phương pháp lặp hội tụ càng nhanh nếu q càng bé. • Áp dụng công thức sai số theo xấp xỉ ban đầu có thể xác định được số lần lặp cần thiết để được nghiệm gần đúng đạt độ chính xác  cho trước.
Nhận xét • Ưu điểm của phương pháp lặp: + Xấp xỉ đầu không nhất thiết phải rất gần nghiệm đúng  (miễn là các điều kiện của định lý được đảm bảo). + Phép lặp có khả năng tự sửa sai: nếu xk tính sai thì coi như chọn lại xấp xỉ đầu mới. + Thuật toán lặp đi lặp lại theo cùng một kiểu, rất thuận lợi khi dùng máy tính. • Nhược điểm: Khi q gần bằng 1, phép lặp hội tụ rất chậm.
Ví dụ Cho phương trình x3 + x – 1000 = 0 với khoảng phân ly nghiệm là (9; 10). 1. Tính đến nghiệm gần đúng x3 của phương trình theo phương pháp lặp, chọn xấp xỉ ban đầu x0 = 10. 2. Đánh giá sai số của nghiệm gần đúng x3.
+ f(x) = x3 + x – 1000 + Xác định hàm lặp . Xét 3 khả năng: 1)x = 1000 – x3 2)x = 1000/x2 – 1/x 3)x = (1000 – x)1/3
Chỉ trường hợp 3) cho phương pháp lặp hội tụ. (x) = (1000 – x)1/3 ; |’(x)| = | 1/3(1000 –x)– 2/3|  q =1/3(1000 – 10)– 2/3  0.0033557
+ Đánh giá sai số của nghiệm gần đúng x3 theo công thức sai số q3 x3 −   x1 − x0 1− q  −9 x3 −   1.2680655*10
Bài tập Cho phương trình x3 + 4x – 3 = 0 và khoảng phân ly nghiệm (0;1). Tính số lần lặp cần thiết để thu được nghiệm gần đúng với sai số tuyệt đối không quá 10 – 3 bằng phương pháp lặp, lấy x0 = 1.
Phương án 1: (x) = (3 – 4x)1/3. Phương pháp lặp không hội tụ Phương án 2: (x) = (3 – x3)/4. Phương pháp lặp hội tụ với q = ¾ Tính x1 = 0,5. Lập bất phương trình suy ra n  27. Phương án 3: (x) = 3/(x2 + 4). Phương pháp lặp hội tụ với q = 6/25