
1
Chương 4: NĂNG LƯỢNG VÀ ĐIỆN THẾ
lTrongchương2và3,chúngtacó 2phươngpháp để tìm điện
trường E:ĐLCoulomb và ĐLGauss.
lDùng ĐLCoulombgiảiđượcnhiềubàitóankhó,nhưng đòi
hỏitínhtóan phứctạp và dài dòng bỡiE là mộttrườngvectơ:
tính 3 tíchphânriêng biệt để xác định 3 thành phần củaE.
lDùng định luậtGauss rấtđơn giản,nhưngtrong trường hợp
điện tíchphân bố đối xứng.
lTrongchương này, sẽ trình bày phương pháp thứ3third để
tìm điện trường E:
Bước1. Xác định1hàmvô hướng bằng phép tính tíchphân
gọi là trường điện thế.
Step2. Tìm Ekhi điện thế bằng phép tính đạo hàm.
1/16/2013 Châu Văn Bảo-ĐHCN TP.HCM
2
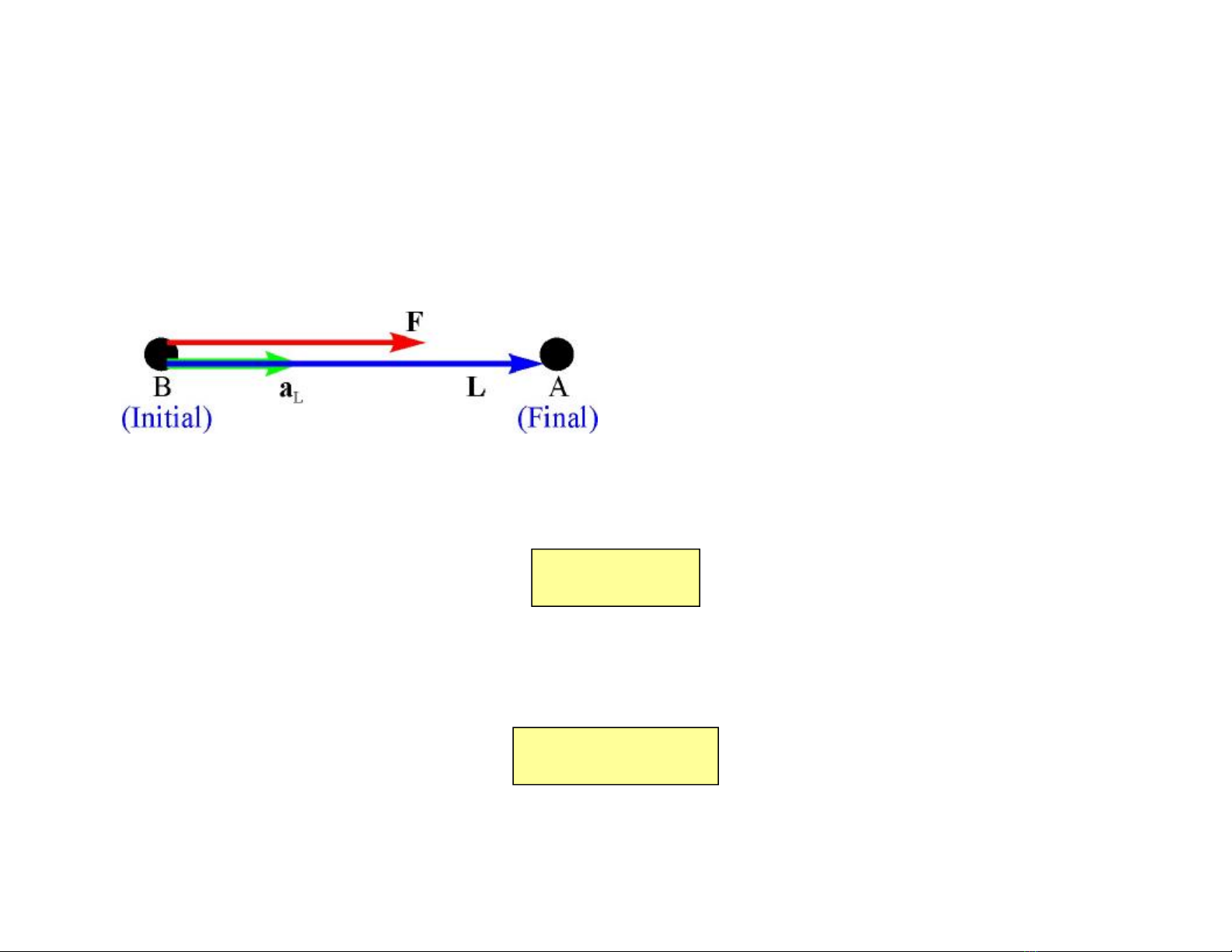
lEđều, L là đọan thẳng, E và
Lcùngphương (FigC4.1)
Vectơdi chuyểnL=lat
Côngcủa ngọai lựcFa
4.1. Công thực hiện để di chuyển điện tích điểm trong
điện trường
MàF
a=-QE
Figure C4.1
W = FaL(C1)
W = Fa . L(C2)
1/16/2013 Châu Văn Bảo-ĐHCN TP.HCM
3
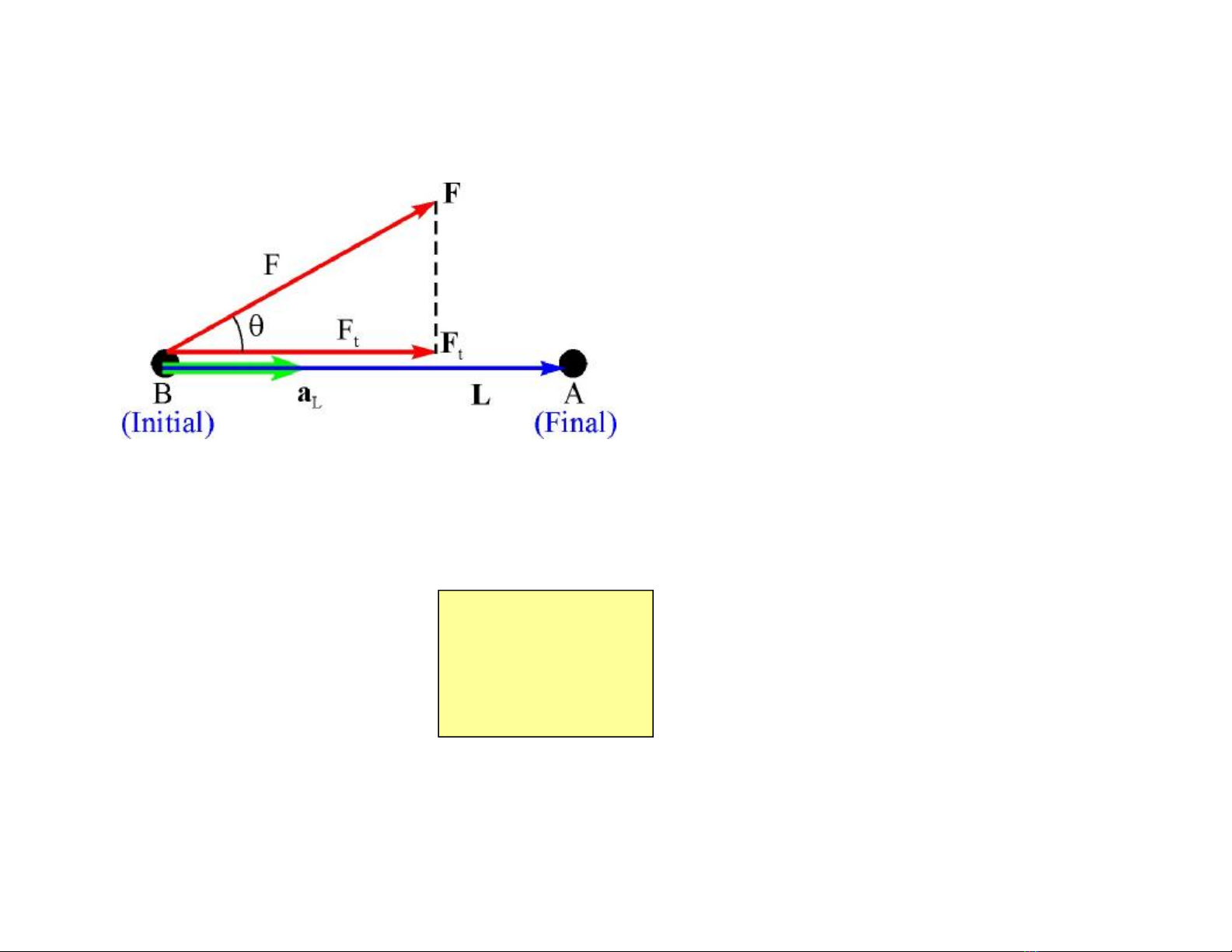
lE đều,L đọan thẳng,E
không cùngphươngL,(Fig
C4.2)
W = FtL
W = FLcosθ
W = F . L
!W>0if0≤θ<π/2;W<0if π/2<θ≤π;W=0if θ=π/2
Figure C4.2
or
or
(C3)
4.1. Công thực hiện để di chuyển điện tích điểm trong
điện trường
1/16/2013 Châu Văn Bảo-ĐHCN TP.HCM
4
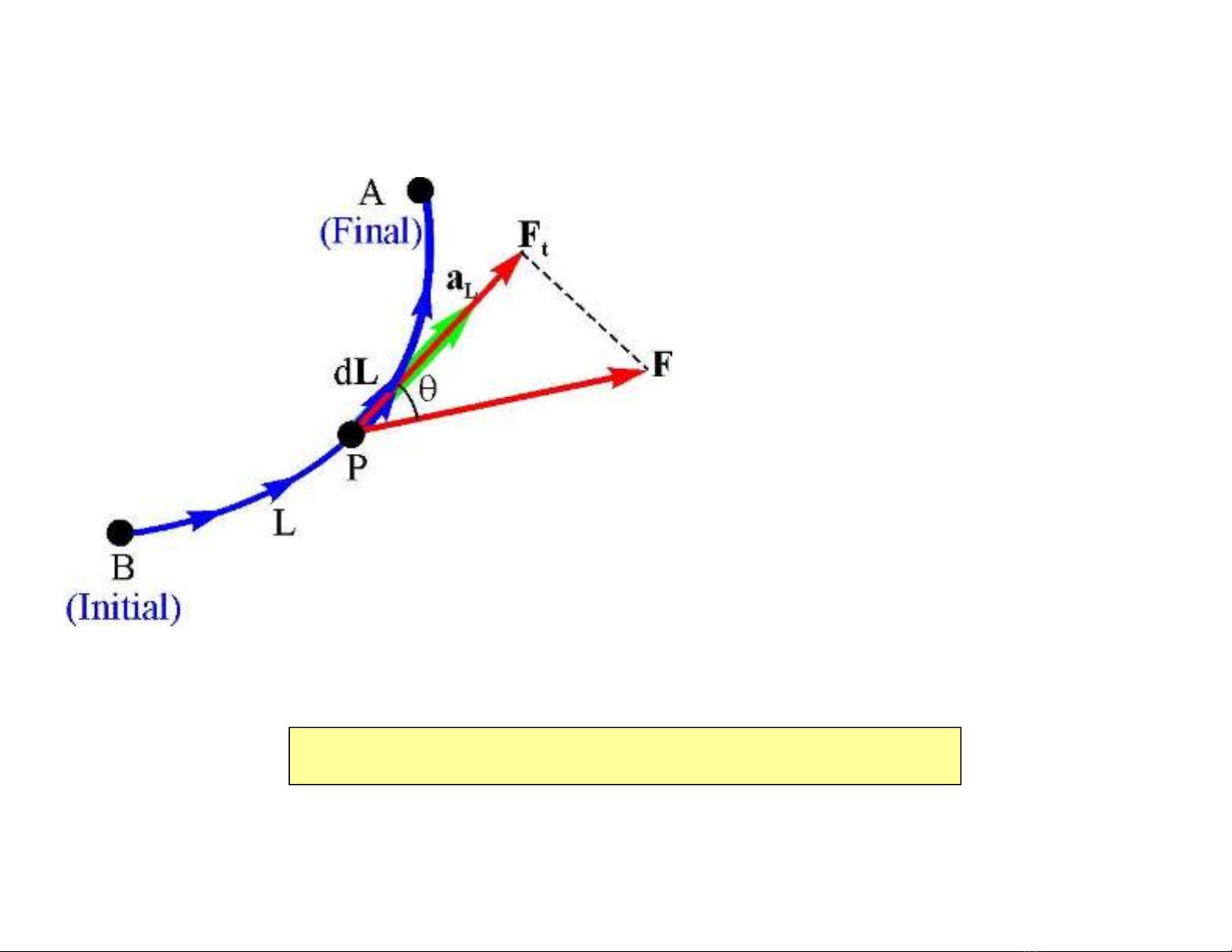
udL rất ngắnnêntrên đọandLtaxemnhưFa đều
dW = FtdL = FdLcosθ=F. dL = - QE.dL
lE không đếu, L không
thẳng.
dL làvectơdi chuyểnvi
phân của diện tích.
dL=dLaL
Figure C 4.3
(C4)
4.1. Công thực hiện để di chuyển điện tích điểm trong
điện trường
1/16/2013 Châu Văn Bảo-ĐHCN TP.HCM
5
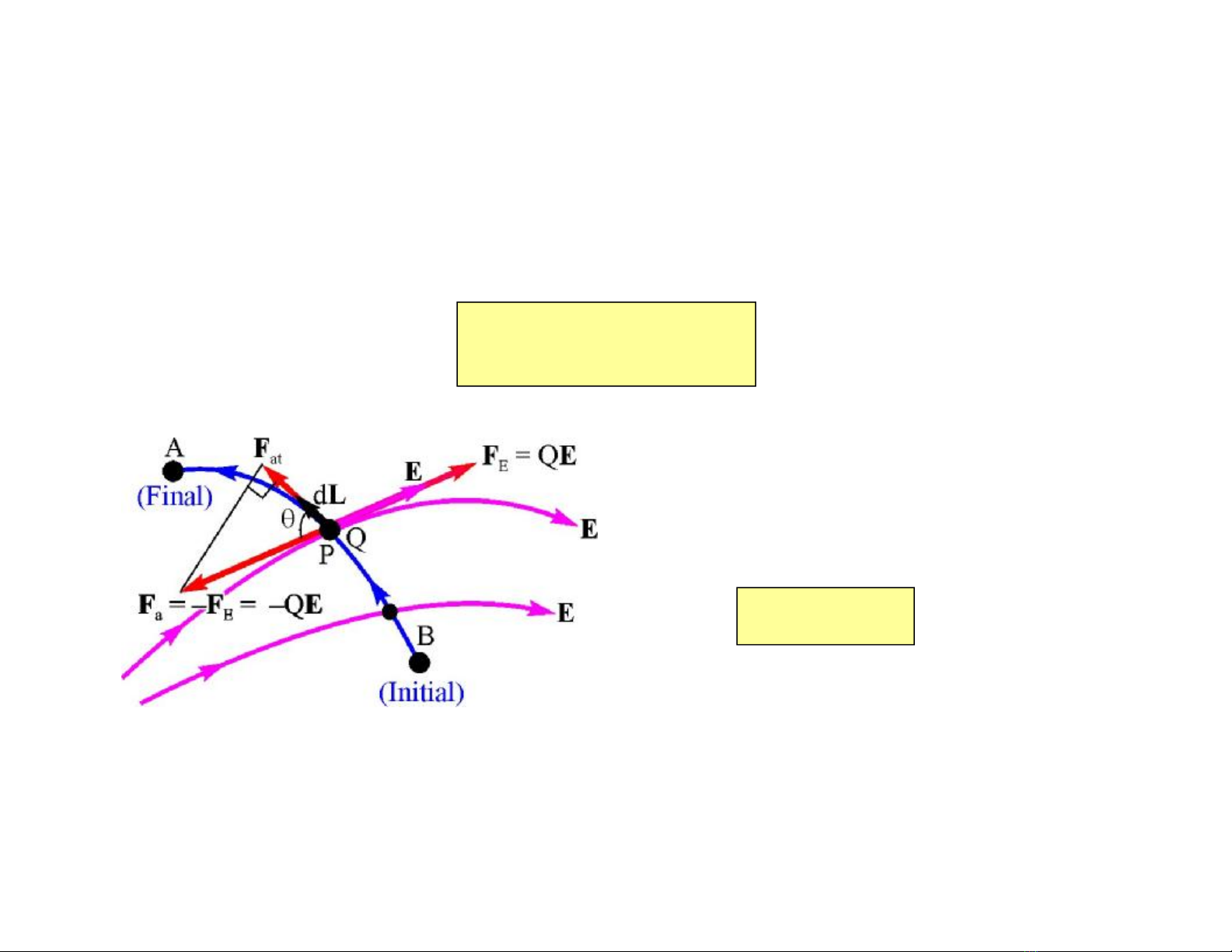
uCông tổngdo ngọai lựcF
a
thực hiện để di chuyểnQ từB đến
AtheoL.
(C5)
E
Q
=
FE
(1)
Figure C.4.4
4.1. Công thực hiện để di chuyển điện tích điểm trong
điện trường
A
B
WQd
=−⋅
∫
EL
1/16/2013 Châu Văn Bảo-ĐHCN TP.HCM


























