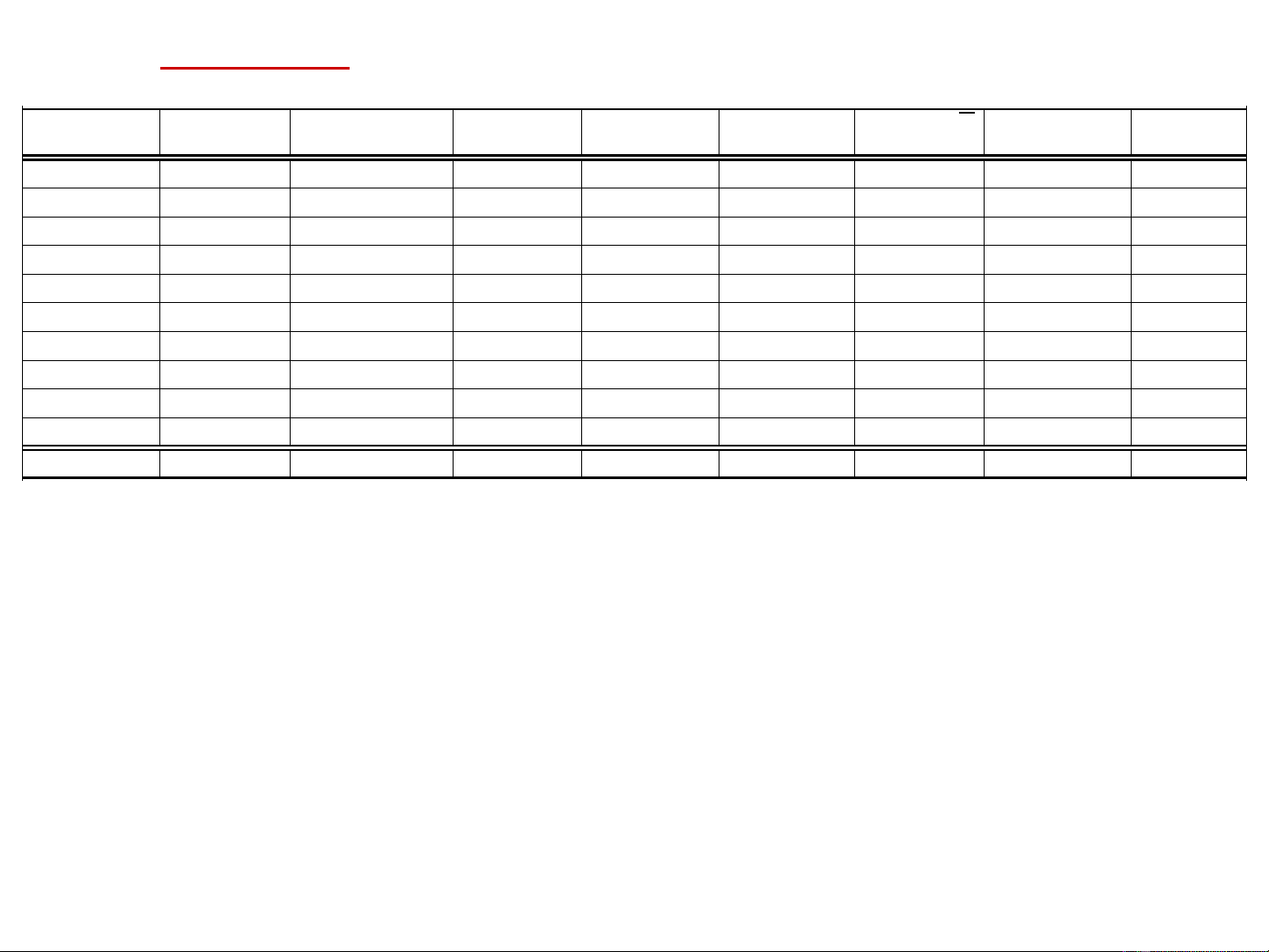
Bài s 1ố
Yi Xi Xi*Yi
3.0 5.0 15.0 25.0 9.0 -7.5 -3.0 22.5 56.3
2.0 4.0 8.0 16.0 4.0 -8.5 -4.0 34.0 72.3
5.0 8.0 40.0 64.0 25.0 -4.5 -1.0 4.5 20.3
10.0 43.0 430.0 1,849.0 100.0 30.5 4.0 122.0 930.3
12.0 18.0 216.0 324.0 144.0 5.5 6.0 33.0 30.3
6.0 9.0 54.0 81.0 36.0 -3.5 0.0 0.0 12.3
3.0 8.0 24.0 64.0 9.0 -4.5 -3.0 13.5 20.3
8.0 12.0 96.0 144.0 64.0 -0.5 2.0 -1.0 0.3
7.0 11.0 77.0 121.0 49.0 -1.5 1.0 -1.5 2.3
4.0 7.0 28.0 49.0 16.0 -5.5 -2.0 11.0 30.3
60.0 125.0 988.0 2,737.0 456.0 0.0 0.0 238.0 1,174.5
2
i
X
2
i
Y
XXx
ii
−=
YYy
ii
−=
ii
yx
2
i
x

a. c l ng hàm h i qui tuy n tínhƯớ ượ ồ ế
1. L p mô hình h i qui tuy n tínhậ ồ ế
S quan sát n=ố10
125/10 = 12.5 6.0000
3.4670
Hàm h i quy m u, c l ng cho hàm h i qui t ng th , có k t qu là:ồ ẫ ướ ượ ồ ổ ể ế ả
P
β
2
t-student
Yi =
5% 0 2.306
60/10 =
238.00
1174.50
2737-10*12.5^2
988-10*12.5*6
6 - 0.2026*12.5
3.467 + ( 0.2026)* Xi +
0.2026
3.467 + ( 0.2026) *Xi
==
∑
n
X
X
i
==
∑
n
Y
Y
i
22 2
( )
i i
i
X Y nX Y
X n X
β
∧
−
= =
−
∑
∑
=
=
=−=
∩∩
XY
21
ββ
=
SRF
i
U
∧
i
Y
∧
=

d. Tìm kho ng tin c y c a h s h i qui v i m c ý ả ậ ủ ệ ố ồ ớ ứ
nghĩa 95%
4. Kho ng tin c yả ậ
( 0.7467 ; 6.1873 )
( 0.0382 ; 0.3671 )
3.467 ± 2.306*1.1796
0.2026 ± 2.306*0.0713
=
/2
( 2)
1 1
( )
n
t se
α
β β
∧ ∧
−
± =
/2
( 2)
2 2
( )
n
t se
α
β β
∧ ∧
−
± =
=
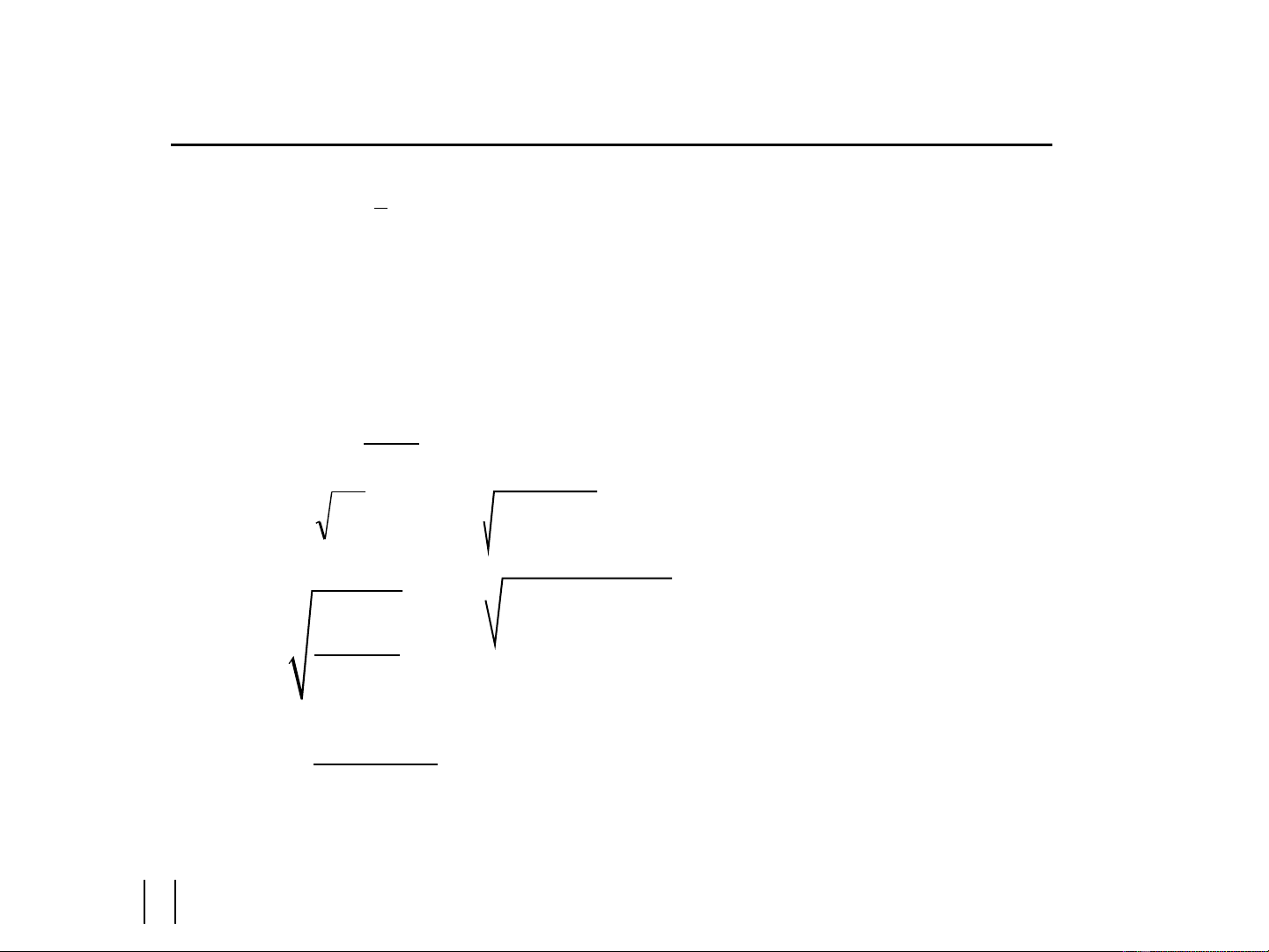
e. Ki m đ nh gi thi t v i m c ý nghĩa 95%ể ị ả ế ớ ứ
2.Ki m đ nh gi thi t h s h i qui c a X trong hàm h i qui t ng th v i m c ý nghĩa 5%ể ị ả ế ệ ố ồ ủ ồ ồ ể ớ ứ
(Ki m đ nh gi thi t: ể ị ả ế
H
0
: β
2
=0H
1
: β
2
≠0 )
96.00
48.23
47.7718
0.50238
5.97148
5.9715 2.44366
5.9715 / 1174.5 0.071300
2.8421
V i m c ý nghĩa α=ớ ứ 0.05 => α/2= 0.025
2.306
2.842
>
2.306 => bác bỏ
H
0
48.2282 / 96
47.7718 / (10- 2 )
0.2026-(0) / 0.0713
456 - 10 * 6^2
0.2026^2 * 1174.5
96 - 48.2282
=−==
∑∑
222
)(YnYyTSS
i
i
=
∑
==
∩
2
2
2i
xESS
β
=
=−=
ESSTSSRSS
=
==
TSSESSR /
2
=
=
−
=
∧
2
2
n
RSS
σ
2
22
( )
i
se x
σ
β
∧
∧
= =
∑
=
=
1,2 0
0
1,2
( )
t
se
β β
β
∧
∧
−
= =
=
=
o
t
=
−
)2(
2/
n
t
α
2
==
∧∧
σσ
=
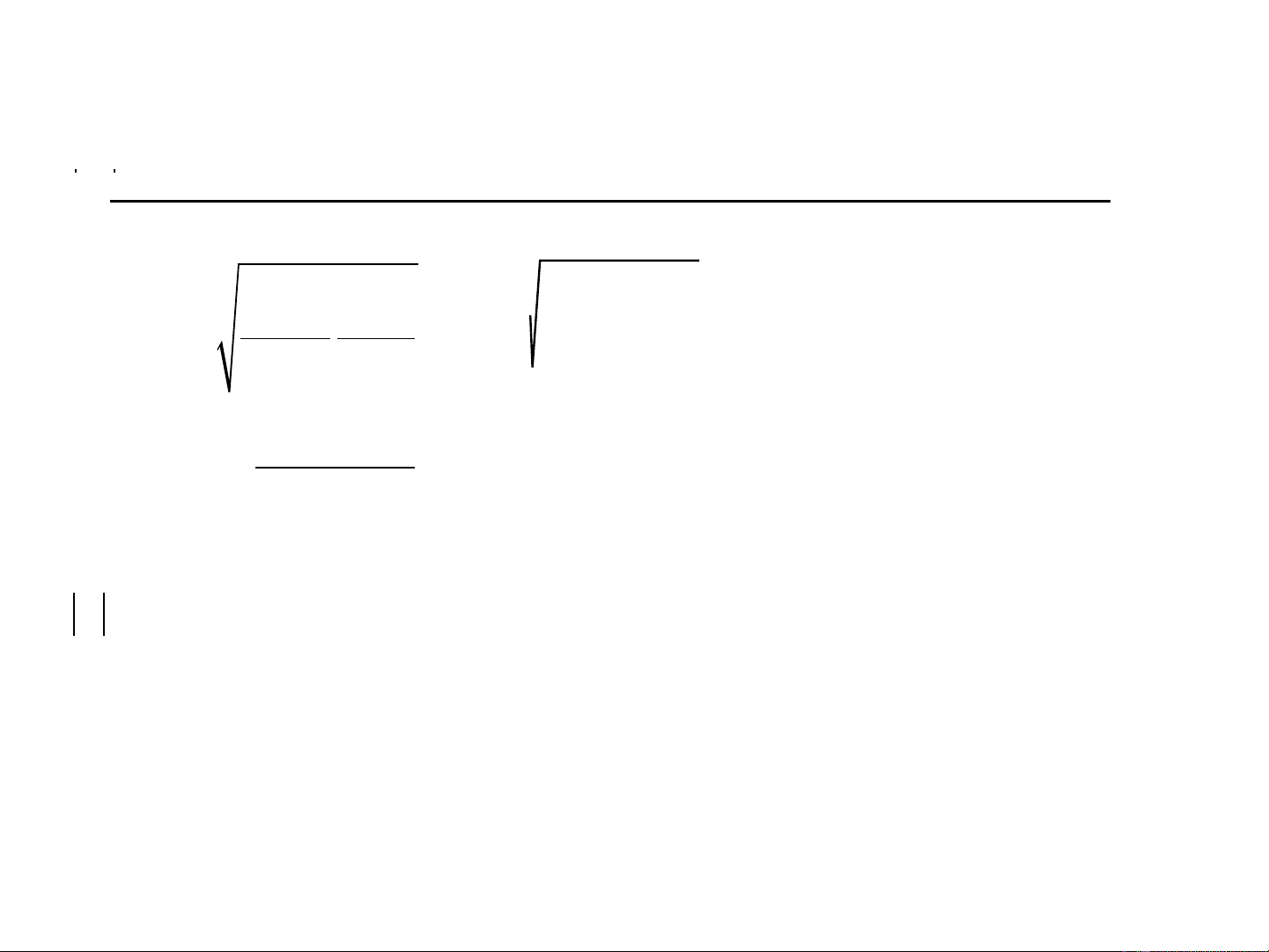
e. Ki m đ nh gi thi t v i m c ý nghĩa 95%ể ị ả ế ớ ứ
3.Ki m đ nh gi thi t h s góc trong hàm h i qui t ng th v i m c ý nghĩa 5%ể ị ả ế ệ ố ồ ồ ể ớ ứ
(Ki m đ nh gi thi t: ể ị ả ế
H
0
: β
1
=0H
1
: β
1
≠0 )
(2737/10) x (5.9715/1174.5) 1.1796
(3.467-0) / 1.1796 2.939
V i m c ý nghĩa α=ớ ứ 0.05 => α/2= 0.025 2.306 P
β
1
2.939
>
2.306 => bác bỏ
H
0
5% 0
=
o
2
2
12
( )
i
i
X
se n x
σ
β
∧
∧
= =
∑∑
1,2 0
0
1,2
( )
t
se
β β
β
∧
∧
−
= =
=
o
t
=
−)2(
2/
n
t
α
=
=


























