
CHUYÊN ĐỀ MẶT CẦU
1
CHUYÊN ĐỀ MẶT CẦU
Mặt cầu ngoại tiếp.
1. Các định nghĩa, định lí và tính chất cơ bản.
Định nghĩa 1. Mặt phẳng trung trực của một đoạn thẳng cho trước là mặt
phẳng qua trung điểm và vuông góc với đoạn thẳng đó.
Tính chất. Nếu M là một điểm bất kì trên mặt phẳng trung trực thì M cách
đều 2 đầu mút của đoạn thẳng đó.
Định nghĩa 2. Trục đường tròn là đường thẳng vuông góc với mặt phẳng
chứa đường tròn và đi qua tâm của đờng tròn đó.
Tính chất. Nếu M là một điểm bất kì trên trục đường tròn thì M cách đều
các điểm của đường tròn.
Từ đó ta có 2 định lí quan trọng:
Định lí1. Trong không gian, tập hợp các điểm cách đều các đỉnh của một đa
giác nội tiếp là trục của đường tròn ngoại tiếp đa giác đó.
Định lí 2. Trong không gian, tập hợp các điềm cách đều các cạnh của một
đa giác ngoại tiếp là trục của đường tròn nội tiếp đa giác đó.
Định nghĩa 3. Mặt cầu ngoại tiếp đa diện là mặt cầu đi qua tất cả các đỉnh
của đa diện. Khi đó ta cũng nói đa diện nội tiếp mặt cầu.
Ta có các nhận xét sau:
- Các mặt của đa diện đều là các đa giác nội tiếp.
- Nếu O là tâm của mặt cầu ngoại tiếp đa diện thì O cách đều tất cả các
cạnh của đa diện. Vì vậy, O nằm trên các trục đường tròn ngoại tiếp
các mặt của đa diện.
- Hiển nhiên nếu O là tâm của mặt cầu ngoại tiếp đa diện thì O nằm trên
các mặt phẳng trung trực của các cạnh của đa diện.
Mặt cầu ngoại tiếp hình chóp và lăng trụ.
1, Hình chóp có một mặt cầu ngoại tiếp khi và chỉ khi đáy của hình chóp là
đa giác nội tiếp.
(Chứng minh. Xét hình chóp S.A1A2…An . Hiển nhiên nếu hình chóp có
mặt cầu ngoại tiếp thì đáy của nó phải là đa giác nội tiếp. Ngược lại nếu đáy
của hình chóp đã cho là đa giác nội tiếp thì ta lấy điểm O trên trục của
đường tròn ngoại tiếp đa giác đáy sao cho OS=OA1. Dễ thấy O chính là tâm
mặt cầu ngoại tiếp hình chóp.)

CHUYÊN ĐỀ MẶT CẦU
2
Từ chứng minh trên, ta thấy nếu hình chóp có mặt cầu ngoại tiếp thì tâm mặt
cầu ngoại tiếp hình chóp chính là giao điểm của mặt phẳng trung trực của
một cạnh bên và trục dường tròn ngoại tiếp đa giác đáy. Đây là một nhận xét
quan trọng để giải bài toán xát định tâm mặt cầu ngoại tiếp hình chóp.
2, Hình lăng trụ có một mặt cầu ngoại tiếp khi và chỉ khi lăng trụ đó là lăng
trụ đứng có đáy là đa giác nội tiếp.
(Chứng minh. Hiển nhiên nếu lăng trụ nội tiếp mặt cầu thì các mặt bên phải
là hình chữ nhật hay lăng trụ đó là lăng trụ đứng và hai đa giác đáy là hai đa
giác ngoại tiếp. Ngược lại nếu có một lăng trụ thoả mãn tính chất lăng trụ đó
là lăng trụ đứng có đáy là đa giác nội tiếp thì ta xét điểm O là trung điểm
đoạn nối tâm 2 đáy. Khi đó dễ thấy O cách đều tất cả các đỉnh của lăng trụ
hay O chính là tâm mặt cầu ngoại tiếp.)
Từ đó ta thấy nếu lăng trụ có mặt cầu ngoại tiếp thì tâm đường tròn ngoại
tiếp lăng trụ đó chính là trung điểm của đoạn nối tâm 2 đường tròn ngoại
tiếp hai đa giác đáy. Đây là một nhận xét quan trọng để giải bài toán xát định
tâm mặt cầu ngoại tiếp lăng trụ.
3, Trong không gian, tập hợp các điểm nhìn đoạn AB dưới một góc vuông là
mặt cầu đường kính AB.
Ví dụ mở đầu.
a, Xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện đều cạnh a.
b, Xác định tâm và bán kính mặt cầu ngoại tiếp tứ diện OABC có OA=a,
OB=b,OC=c và OA,OB,OC đôi một vuông góc.
Giải.
a,
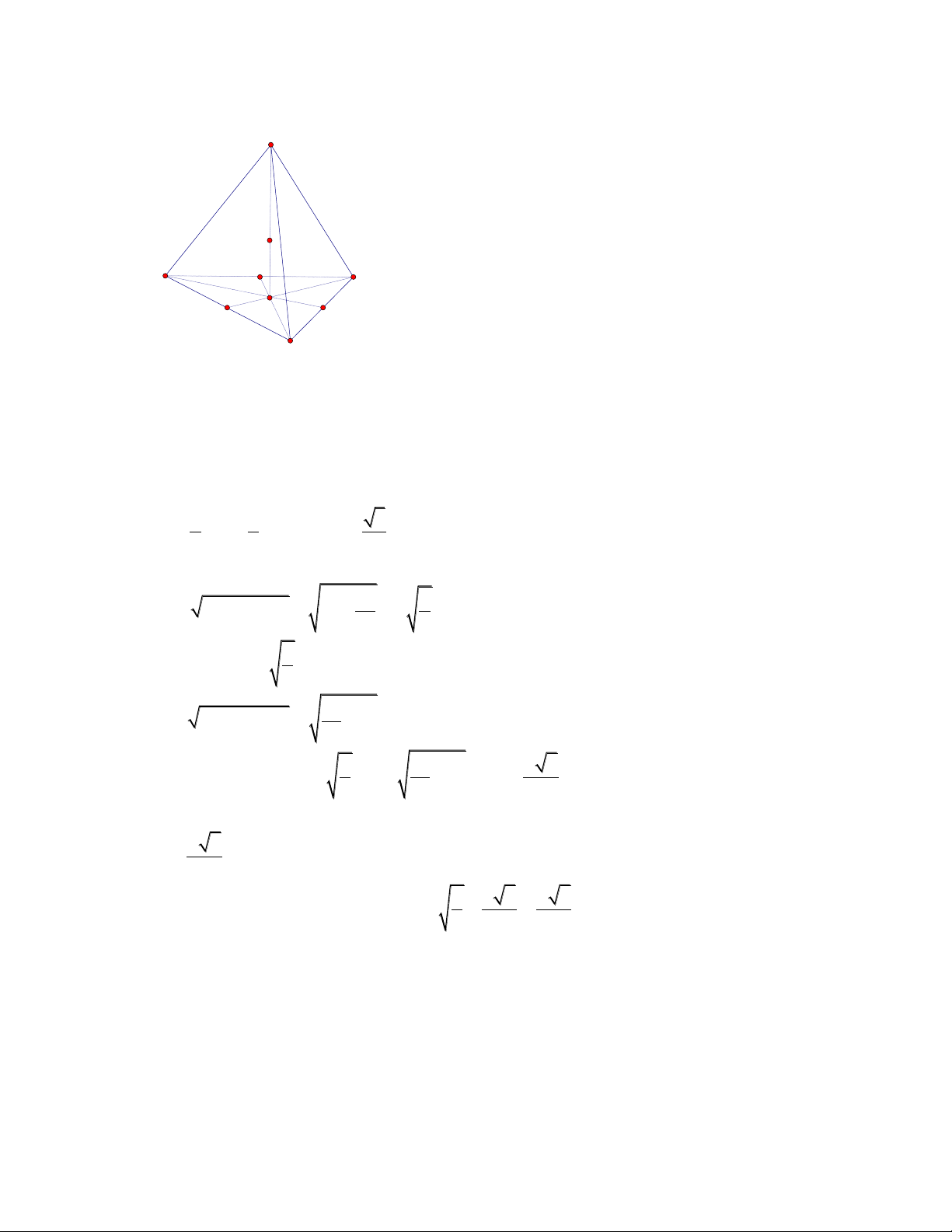
CHUYÊN ĐỀ MẶT CẦU
3
Gọi H là tâm của tam giác đều BCD. Dễ thấy A nằm trên trục của đường
tròn ngoại tiếp ∆BCD. Gọi O là tâm của mặt cầu ngoại tiếp ABCD thì O
nằm trên AH. Đặt OH=x (x>0)
Ta có.
0
2 2 3
.sin 60 .
3 3 3
BH BE a a
2
2 2 2 2
33
a
AH AB BH a a
2
3
OA AH x a x
2
2 2 2
3
a
BO BH HO x
Ta được
2
2
26
3 3 12
aa
OA OB a x x x
vậy tâm O của mặt cầu ngoại tiếp nằm trên AH và cách (BCD) một khoảng
OH=
6
12
a
Bán kính của mặt cầu là R=OA=
2 6 6
3 12 4
aa
a
.
b,
H
B
A
C
D
O
E

CHUYÊN ĐỀ MẶT CẦU
4
O
M
C
S
A
B
H
Gọi H là trung điểm của AB. Dễ thấy H là tâm đường tròn ngoại tiếp ∆SAB.
Mặt phẳng trung trực của SC cắt trục đường tròn (SAB) tại O. Ta có O chính
là tâm mặt cầu ngoại tiếp tứ diện SABC. Dễ thấy OH=
2
c
.
R=
2
22 2 2 2
2 2 2 2
4 4 2
AB SA SB a b c
SO SH HO HO HO
Qua bài toán mở đầu ta có nhận xét rằng để giải bài toán xác định tâm và
bán kính mặt cầu ngoại tiếp thì cách thông dụng nhất là sử dụng định nghĩa
(tâm mặt cầu ngoại tiếp cách đều các đỉnh của đa diện) hoặc sử dụng tính
chất của tâm mặt cầu ngoại tiếp (tâm mặt cầu ngoại tiếp nằm trên trục của
đường tròn ngoại tiếp các mặt đa diện). Đây là 2 cách thông dụng nhất trong
việc xác định tâm và bán kính của mặt cầu ngoại tiếp đa diện nội tiếp.
Sau đây ta sẽ đi sâu vào xem xét và giải quyết các bài toán về mặt cầu ngoại
tiếp và một phương pháp mới hơn để xác định tâm và bán kính mặt cầu
ngoại tiếp đa diện bất kì. Ta tạm gọi đó là Phương pháp tạo lăng trụ bao.
Ta tạo các lăng trụ quen thuộc để dễ dàng hơn trong việc xác định tâm hay
tính toán các yếu tố của mặt cầu ngoại tiếp đa diện.
Để hiểu được ý nghĩa của phương pháp này, ta đi xét các ví dụ sau.
Đầu tiên ta giải ví dụ mở đầu (câu b) bằng phương pháp này.
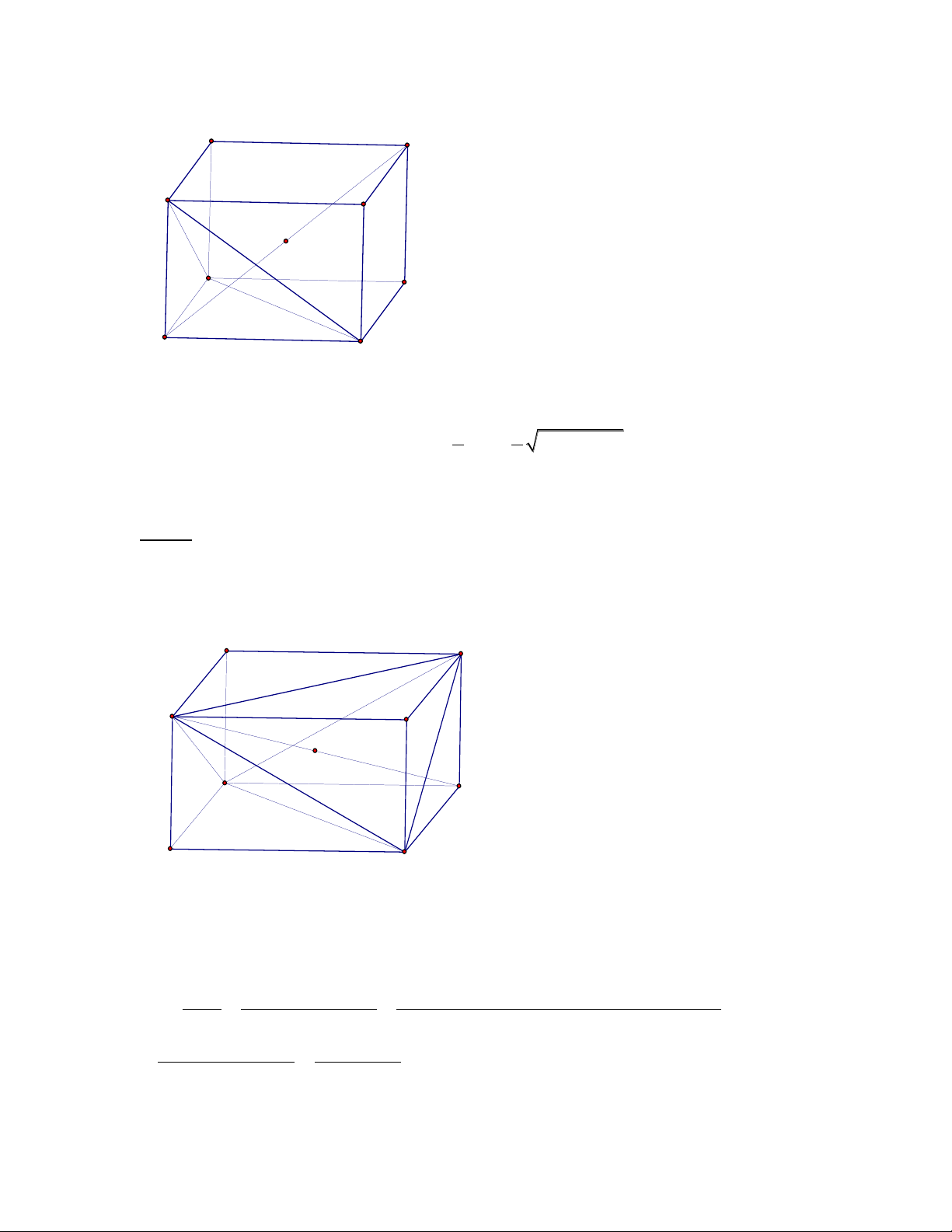
Bài 1.
CHUYÊN ĐỀ MẶT CẦU
5
O
W
U
V
T
S
A
B
C
Mở rộng tứ diện SABC thành hình hộp chữ nhật SATB.CWUV. Dễ thấy
rằng tâm O của mặt cầu ngóại tiếp tứ diện SABC chính là tâm của hình hộp
chữ nhật SATB.CWUV. Do đó
222
11
22
R SU a b c
.
Bài 2.
Cho tứ diện ABCD có tính chất AB=CD=a, BC=AD=b,CA=BD=c. Tính
diện tích mặt cầu ngoại tiếp tứ diện đó.
O
C
1
C
D
1
B
1
E
1
B
D
A
Mở rộng tứ diện ABCD thành hình hộp chữ nhật AB1CC1.E1DD1B như hình
vẽ. Dễ nhận ra rằng tâm O của mặt cầu ngoại tiếp tứ diện ABCD chính là
tâm của hình hộp chữ nhật AB1CC1.E1DD1B .
Do đó ta có:
2 2 2 2 2 2 2 2 2 2
21 1 1 1 1 1 1 1 1 1
2 2 2 2 2 2
( ) ( ) ( )
4 4 8
88
AD AB AC AE AB AC AC AE AE AB
R
AC AB AD abc


























