
M ĐUỞ Ầ
C u trúc không gian c a phân t nh h ng đn tính ch t c a m t ch t. ấ ủ ử ả ưở ế ấ ủ ộ ấ Hóa h c l p th làọ ậ ể
ngành chuyên nghiên c u v c u trúc không gian c a các phân t , nh h ng không gian c a phân tứ ề ấ ủ ử ả ưở ủ ử
đn tính ch t c a các ch t cũng nh nghiên c u v h ng không gian trong các ph n ng hóa h c.ế ấ ủ ấ ư ứ ề ướ ả ứ ọ
L ch s phát tri n c a hóa h c l p th g n li n v i l ch s phát tri n c a hóa h c h u c . Cácị ử ể ủ ọ ậ ể ắ ề ớ ị ử ể ủ ọ ữ ơ
nghiên c u v hóa h c l p th m i đu ch gi i h n trong hóa h c l p th c u hình nh ng sau đóứ ề ọ ậ ể ớ ầ ỉ ớ ạ ọ ậ ể ấ ư
các v n đ c a hóa h c l p th ngày càng ph c t p, đc bi t do s phát tri n c a h c thuy t v c uấ ề ủ ọ ậ ể ứ ạ ặ ệ ự ể ủ ọ ế ề ấ
d ng và phân tích c u d ng, v hóa h c l p th c a ph n ng, v s t ng h p đnh h ng l p thạ ấ ạ ề ọ ậ ể ủ ả ứ ề ự ổ ợ ị ướ ậ ể
và ch n l a l p th . Tuy nhiên nh s xu t hi n các ph ng pháp v t lý nh ph h ng ngo i, phọ ự ậ ể ờ ự ấ ệ ươ ậ ư ổ ồ ạ ổ
phân c c, ph c ng h ng t h t nhân, nhi u x tia X,...các nghiên các nghiên c u v hóa h c l pự ổ ộ ưở ừ ạ ễ ạ ứ ề ọ ậ
th đã cho ta nhi u hi u bi t m i v s ph thu c c a các tính ch t và nh ng đc tính tinh vi v sể ề ể ế ớ ề ự ụ ộ ủ ấ ữ ặ ề ự
phân b không gian c a các nguyên t trong phân t , trong vi c gi i thích c ch c a nhi u ph nố ủ ử ử ệ ả ơ ế ủ ề ả
ng.ứ
Hóa h c l p th có ý nghĩa th c t r t l n đc bi t trong lĩnh v c hóa h c các h p ch t thiênọ ậ ể ự ế ấ ớ ặ ệ ự ọ ợ ấ
nhiên, trong t ng h p các h p ch t quang ho t v i c u hình đnh s n c n cho y h c và sinh h c, nh tổ ợ ợ ấ ạ ớ ấ ị ẵ ầ ọ ọ ấ
là nh ng nhóm h p ch t có ho t tính cao nh prostaglandin, pheromon. Tính ch t c a các ch tữ ợ ấ ạ ư ấ ủ ấ
polime t ng h p ph thu c r t nhi u vào c u t o không gian c a chúng. Hi n nay vi c đi u ch cácổ ợ ụ ộ ấ ề ấ ạ ủ ệ ệ ề ế
polime có d ng l p th xác đnh là m t trong nh ng ph ng pháp quan tr ng nh t đ tăng ph mạ ậ ể ị ộ ữ ươ ọ ấ ể ẩ
ch t c a các v t li u nhân t o.ấ ủ ậ ệ ạ
S ti n b nhanh chóng c a hóa h c l p th - t vi c t ng h p đc urê c a Wohler nămự ế ộ ủ ọ ậ ể ừ ệ ổ ợ ượ ủ
1828, đn các công trình t ng h p c a Kolbe năm 1840; c a Berthelot năm 1850 đã đt n n t ngế ổ ợ ủ ủ ặ ề ả
khoa h c cho hóa h c h u c và d n đn vi c xây d ng m t c s lý thuy t cho khoa h c hóa h uọ ọ ữ ơ ẫ ế ệ ự ộ ơ ở ế ọ ữ
c .ơ
Hóa học lập thể, đặc biệt là các đồng phân quang học và các hợp chất quang hoạt có ý nghĩa
th c t to l n và đc ng d ng trong nhi u lĩnh v c quan tr ng. Vì v y, tôi ch n tìm hi u đ tài vự ế ớ ượ ứ ụ ề ự ọ ậ ọ ể ề ề
“các h p ch t quang ho t vàợ ấ ạ đng phân quang h cồ ọ ”.
Vì nhi u lý do nên đ tài ch c còn nhi u thi u sót, mong th y và các b n đc đóng góp ýề ề ắ ề ế ầ ạ ọ
ki n, đ đ tài c a tôi hoàn ch nh h n.ế ể ề ủ ỉ ơ
Xin chân thành c m n.ả ơ
Ti u lu n Hóa l p th : Đng phân quang h cể ậ ậ ể ồ ọ
PH N N I DUNGẦ Ộ
C s v t lý c a v n đ quang ho tơ ở ậ ủ ấ ề ạ
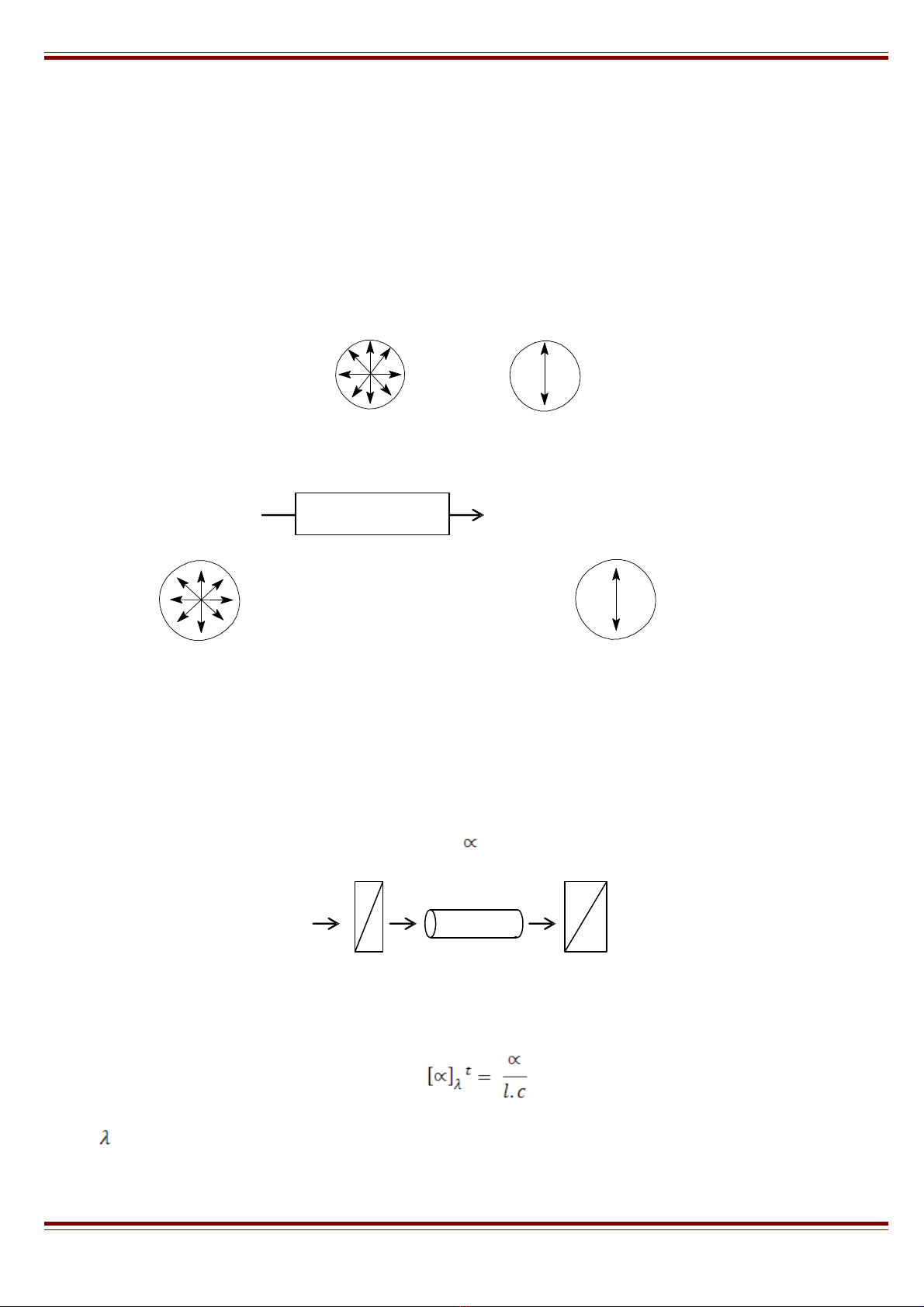
Ánh sáng là m t sóng đi n t mà ph ng dao đng luôn th ng góc v i ph ng truy n sóng.ộ ệ ừ ươ ộ ẳ ớ ươ ề
Các dao đng c a ánh sáng th ng th ng góc v i ph ng truy n sóng và h ng ra xung quanh theoộ ủ ườ ẳ ớ ươ ề ướ
m i m t ph ng trong không gian. Ánh sáng phân c c ph ng là ánh sáng mà vect đi n tr ng c aọ ặ ẳ ự ẳ ơ ệ ườ ủ
t t c sóng ánh sáng đu h ng theo m t ph ng, có nghĩa là cùng n m trên m t m t ph ng, m tấ ả ề ướ ộ ươ ằ ộ ặ ẳ ặ
ph ng này g i là m t ph ng phân c c.ẳ ọ ặ ẳ ự
aùnh saùng thöôøng aùnh saùng phaân cöïc phaúng
Ánh sáng phân c c ph ng có th đc t o nên b i ánh sáng th ng chi u qua m t kính phân ự ẳ ể ượ ạ ở ườ ế ộ
c c, ch ng h n kính Nicol.ự ẳ ạ
Ánh sáng thường
Kính phân cực
Ánh sáng phân cực phẳng
Có m t s ch t h u c có kh năng làm quay m t ph ng ánh sáng phân c c khi cho ánh sángộ ố ấ ữ ơ ả ặ ẳ ự
phân c c đi qua. Kh năng đó g i là tính quang ho t, còn nh ng ch t có kh năng đó g i là ch tự ả ọ ạ ữ ấ ả ọ ấ
quang ho t. N u m t ch t làm quay m t ph ng phân c c theo chi u kim đng h đc g i là ch tạ ế ộ ấ ặ ẳ ự ề ồ ồ ượ ọ ấ
quay ph i. N u m t ch t làm quay m t ph ng phân c c ng c chi u kim đng h đc g i là ch tả ế ộ ấ ặ ẳ ự ượ ề ồ ồ ượ ọ ấ
quay trái. Giá tr đ quay m t ph ng phân c c đc di n t b ng góc quay và d u (+) đng tr cị ộ ặ ẳ ự ượ ễ ả ằ ấ ứ ướ
di n t chi u quay ph i, d u (-) đng tr c di n t chi u quay trái.ễ ả ề ả ấ ứ ướ ễ ả ề
Đ đo kh năng làm quay m t ph ng m t ph ng phân c c (đ quay c c) c a các ch t quangể ả ặ ẳ ặ ẳ ự ộ ự ủ ấ
ho t ng i ta dùng phân c c k ghi l y góc quay ạ ườ ự ế ấ . Đc và so sánh giá tr quay t ng ng khi có vàọ ị ươ ứ
không có m u ch t đng trong ng.ẫ ấ ự ố
Ánh sáng
đn sơ ắc
Lăng kính
Nicol
ống mẫu
Lăng kính Nicol đặt trên
đĩa tròn quay
Đi v i m t ch t quang ho t ng i ta th ng dùng đi l ng đ quay c c riêng [ ]. Đ quayαố ớ ộ ấ ạ ườ ườ ạ ượ ộ ự ộ
c c riêng c a m t ch t trong dung d ch đc tính theo công th c:ự ủ ộ ấ ị ượ ứ
là góc quay quan sát đc đi v i m t dung d ch có b dày l dm. ượ ố ớ ộ ị ề
Đ dài sóng c a ánh sáng, t nhi t đ t i th i đi m đo.ộ ủ ệ ộ ạ ờ ể
H c viên: Nguy n Xuân Phongọ ễ 2
Ti u lu n Hóa l p th : Đng phân quang h cể ậ ậ ể ồ ọ
C u hình tuy t đi c a m t h p ch t có th xác đnh b ng tia X. Tr c kia khi bi t đc c uấ ệ ố ủ ộ ợ ấ ể ị ằ ướ ế ượ ấ
hình tuy t đi c a m t s ch t ho t đng quang h c, c u hình c a m t ch t khác có th đc xácệ ố ủ ộ ố ấ ạ ộ ọ ấ ủ ộ ấ ể ượ
đnh b ng m i t ng quan hóa h c v i ch t đã bi t c u trúc.ị ằ ố ươ ọ ớ ấ ế ấ
Đng phân quang h cồ ọ
Đng phân quang h c là nh ng h p ch t có công th c c u t o ph ng gi ng nhau nh ng khácồ ọ ữ ợ ấ ứ ấ ạ ẳ ố ư
nhau v c u trúc không gian do trong phân t có y u t không trùng v t nh, hay phân t có s b tề ấ ử ế ố ậ ả ử ự ấ
đi x ng. Nh ng đng phân này ch khác nhau v tính ho t đng quang ho t, nghĩa là kh năng quayố ứ ữ ồ ỉ ề ạ ộ ạ ả
m t ph ng phân c c khác nhau.ặ ẳ ự
Các y u t đi x ng phân tế ố ố ứ ử
Tính ch t c a m t phân t nào đó có th đc xác đnh b ng s có m t hay không có nh ngấ ủ ộ ử ể ượ ị ằ ự ặ ữ
y u t đi x ng c b n. Quan tr ng nh t là nh ng y u t đi x ng sau:ế ố ố ứ ơ ả ọ ấ ữ ế ố ố ứ
3.1. M t ph ng đi x ngặ ẳ ố ứ
M t ph ng đi x ng (th ng ký hi u m) là m t ph ng chia v t ra làm hai ph n mà ph n nàyặ ẳ ố ứ ườ ệ ặ ẳ ậ ầ ầ
là nh c a ph n kia trong g ng. Phân t có m t ph ng đi x ng n u sau khi chi u vào m t ph ngả ủ ầ ươ ử ặ ẳ ố ứ ế ế ặ ẳ
thì nh s trùng v i nó:ả ẽ ớ
H
H
Cl
Cl
H
H
H
Cl
Cl
H
H
3.2. Tâm đi x ngố ứ
Tâm đi x ng (i) là đi m mà trên đng th ng đi qua đi m đó có th g p đc nh ng đi mố ứ ể ườ ẳ ể ể ặ ượ ữ ể
t ng đng kho ng cách nh nhau ho c là đi m mà khi quay phân t đi x ng đi m đó thu đcươ ươ ở ả ư ặ ể ử ố ứ ể ượ
nh trùng v i v t ban đu.ả ớ ậ ầ
Th ng m t v t có th có nhi u m t ph ng đi x ng, nh ng th ng ch có m t tâm điườ ộ ậ ể ề ặ ẳ ố ứ ư ườ ỉ ộ ố
x ng.ứ
b
a
a'
b'
i
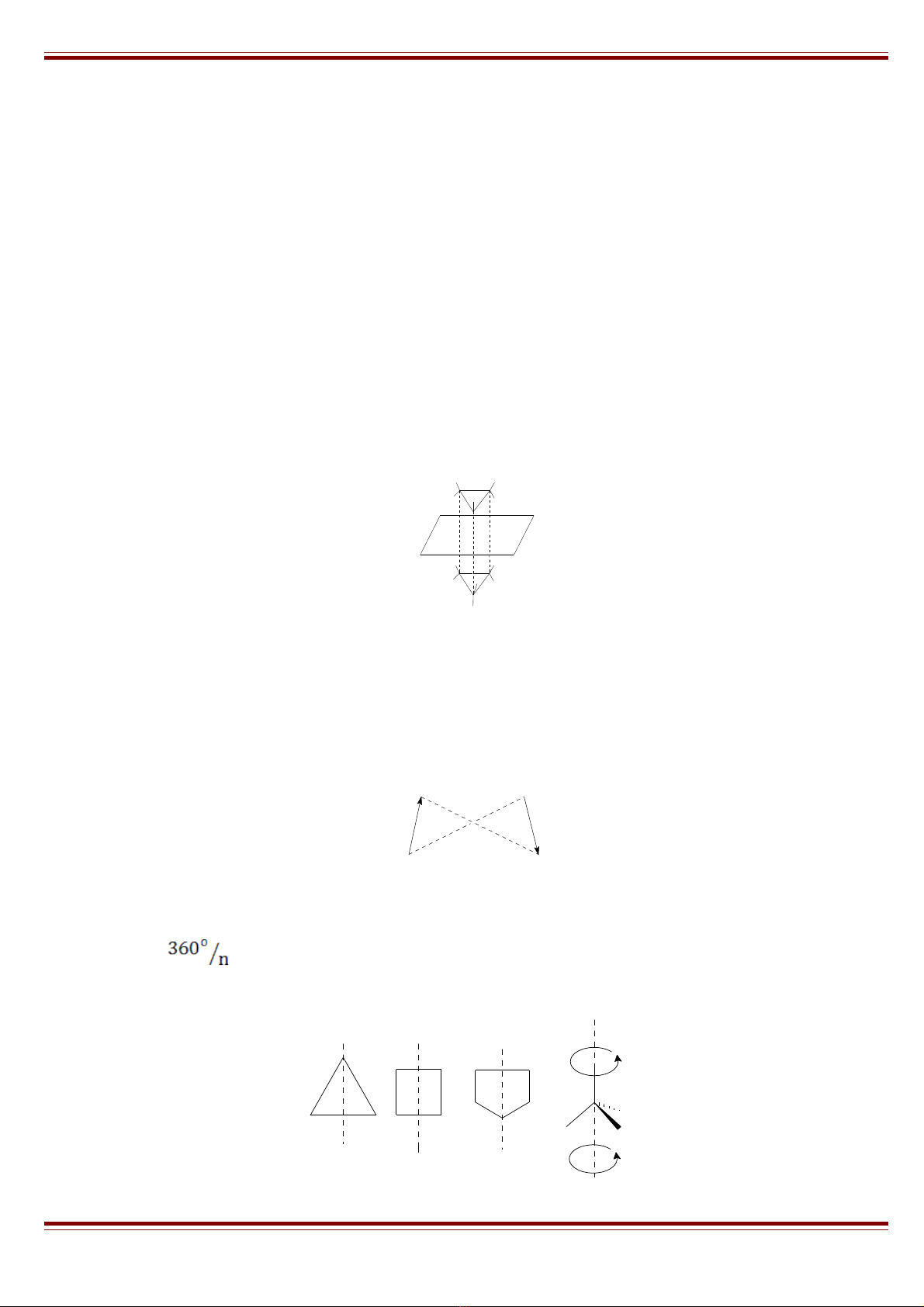
3.3. Tr c đi x ngụ ố ứ
Tr c đi x ng (th ng g i là tr c C) là tr c đi qua v t mà n u quay xung quanh tr c m t gócụ ố ứ ườ ọ ụ ụ ậ ế ụ ộ
xác đnh b ngị ằ thì thu đc c u trúc trùng v i c u trúc ban đu. B c c a tr c ph thu c vàoượ ấ ớ ấ ầ ậ ủ ụ ụ ộ
giá tr c a n. Tr c b c 1 khi quay 360ị ủ ụ ậ o, tr c b c 1 v i n = 1, tr c Cụ ậ ớ ụ 2 – 180o v i n = 2, ...ớ
C3C4C5
Cl
H
Cl
Cl
H c viên: Nguy n Xuân Phongọ ễ 3
Ti u lu n Hóa l p th : Đng phân quang h cể ậ ậ ể ồ ọ
Trong phân t có tr c liên h p C n u sau khi quay xung quanh tr c r i chi u vào m t ph ngử ụ ợ ế ụ ồ ế ặ ẳ
th ng góc v i tr c thì thu đc v t trùng v i ch t ban đu:ẳ ớ ụ ượ ậ ớ ấ ầ
C C
H
Cl
Cl
H
C C
Cl
H
H
Cl
C C
H
Cl
Cl
H
Ngoài các y u t đi x ng trên còn dùng nhóm đi x ng, trong 15 nhóm có ba nhóm quanế ố ố ứ ố ứ
tr ng có tính không trùng v t nh g i là nhóm Cọ ậ ả ọ 1, Cn và nhóm D2. Ta hay g p nhóm Cặ1, trong đó phân
t không c y u t đi x ng nào, ch ng h n đi v i cacbon liên k t v i b n nhóm th khác nhau,ử ố ế ố ố ứ ẳ ạ ố ớ ế ớ ố ế
không có y u t đi x ng nào g i là cacbon b t đi, ho c nhóm Cế ố ố ứ ọ ấ ố ặ n trong phân t có tr c n l ho cử ụ ẻ ặ
m t tr c b c n v i vài tr c Cộ ụ ậ ớ ụ 2 và nhóm D2 dùng trong tính quang h c c a các đng phân c u d ng.ọ ủ ồ ấ ạ
Phân t b t đi có m t nguyên t cacbon b t điử ấ ố ộ ử ấ ố
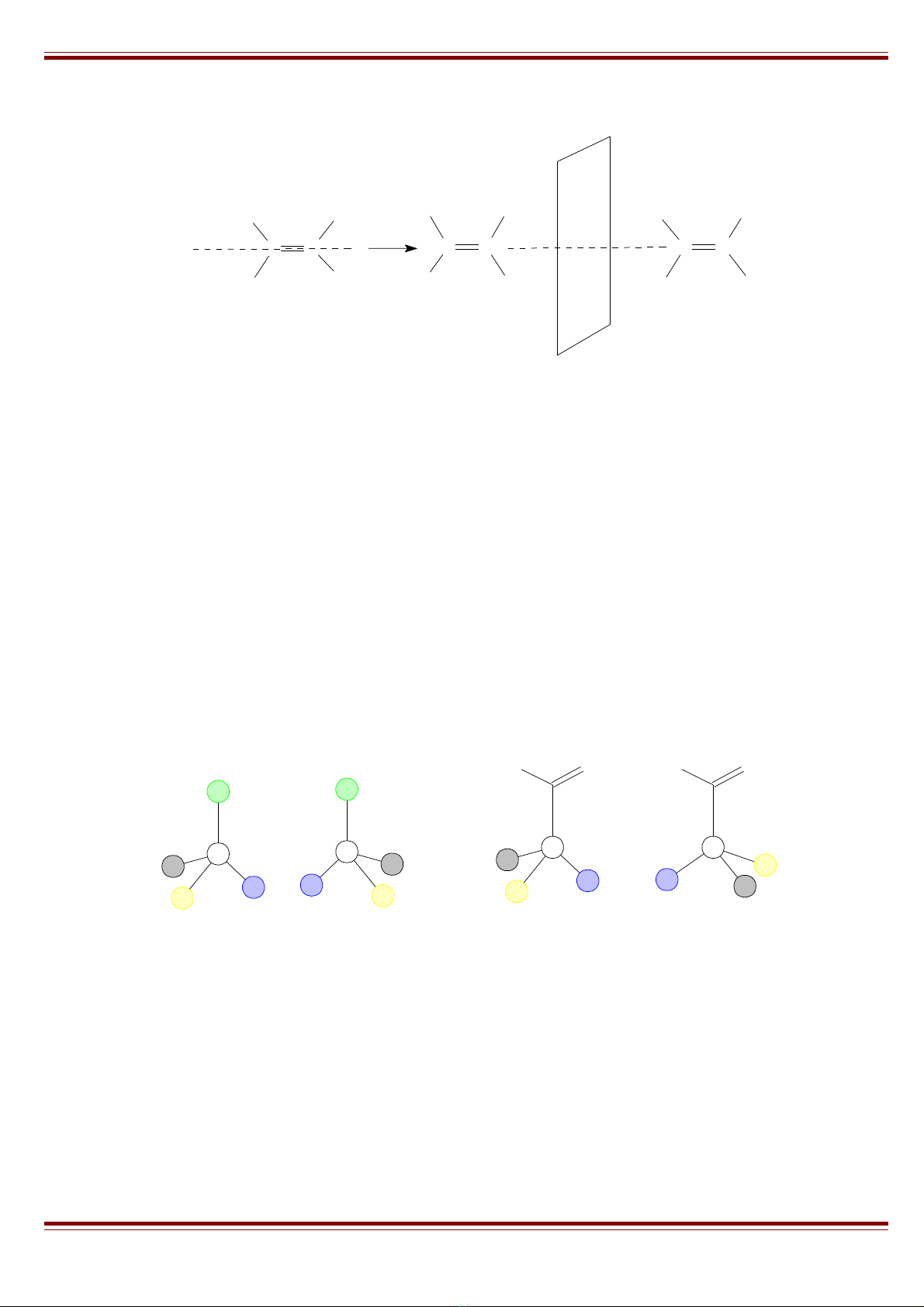
Trong phân t có m t nguyên t C liên k t v i 4 nhóm th hoàn toàn khác nhau. Hi n nayử ộ ử ế ớ ế ệ
nguyên t C này đc g i là trung tâm l p th .ử ượ ọ ậ ể
4.1. Đi quang hay enantiomerố
Hai phân t có c u hình khác nhau mà ch t này là nh c a ch t kia trong m t ph ng g ngử ấ ấ ả ủ ấ ặ ẳ ươ
g i là m t c p đi quang (ngh ch quang) hay enantiomer. Hai ch t này không ch ng khít lên nhauọ ộ ặ ố ị ấ ồ
đc tuy chúng có tính ch t v t lý và hóa h c gi ng nhau. Hai ch t này ch khác nhau v c u hình,ượ ấ ậ ọ ố ấ ỉ ề ấ
hai c u hình này ng c nhau:ấ ượ
O
HO
H
Khaùc nhau veà caáu daïng, gioáng nhau veà caáu hình
khoâng phaûi laø enantiomer
Khaùc nhau veà caáu hình
laø enantiomer
Hai enantiomer hay hay đi quang là hai đng phân l p th c a nhau, có c u hình ng c nhauố ồ ậ ể ủ ấ ượ
nên h ng quay m t ph ng ánh sáng phân c c ng c nhau nh ng có cùng giá tr tuy t đi (vì cùngướ ặ ẳ ự ượ ư ị ệ ố
c u trúc c a trung tâm b t đi x ng). Còn nh ng đng phân l p th khác có c u hình khác nhau vấ ủ ấ ố ứ ữ ồ ậ ể ấ ề
nh và v t trong m t ph ng g ng là đng phân quang h c c a nhau, không ph i là enantiomer c aả ậ ặ ẳ ươ ồ ọ ủ ả ủ
nhau mà đng phân đi-a c a nhau, th ng g p trong nh ng phân t có hai hay nhi u trung tâm b tồ ủ ườ ặ ữ ử ề ấ
đi x ng.ố ứ
4.2. Bi n th raxemicế ể
Bi n th raxemic là m t t p h p đng phân t (equimolar) hai ch t đi quang, tr s quay c cế ể ộ ậ ợ ẳ ử ấ ố ị ố ự
c a t p h p này b ng không vì có s bù tr nhau gi a hai d ng D và L. Bi n th raxemic th ngủ ậ ợ ằ ự ừ ữ ạ ế ể ườ
H c viên: Nguy n Xuân Phongọ ễ 4
Ti u lu n Hóa l p th : Đng phân quang h cể ậ ậ ể ồ ọ
đc ký hi u là DL ho c (ượ ệ ặ ).
4.2.1. S t o thành bi n th raxemicự ạ ế ế
Ph ng pháp tr n l nươ ộ ẫ
Tr n k các l ng b ng nhau c a hai ch t đi quang.ộ ỹ ượ ằ ủ ấ ố
Ph ng pháp t ng h pươ ổ ợ
Ph ng pháp raxemic hóaươ
4.2.2. Tính ch t c a các bi n th raxemicấ ủ ế ể
tr ng thái khí, l ng cũng nh dung d ch, bi n th raxemic là m t h n h p c a nh ng l ngỞ ạ ỏ ư ị ế ể ộ ỗ ợ ủ ữ ượ
b ng nhau g n nh lý t ng c a các phân t đi quang. Bi n th raxemic có cùng nhi t đ sôi nhằ ầ ư ưở ủ ử ố ế ể ệ ộ ư
ch t đi quang tinh khi t, chi t su t và t tr ng tr ng thái l ng là gi ng nhau cũng nh ph h ngấ ố ế ế ấ ỉ ọ ở ạ ỏ ố ư ổ ồ
ngo i tr ng thái l ng và dung d ch là trùng nhau.ạ ở ạ ỏ ị
Tuy nhiên s đng nh t này không th áp d ng đi v i tr ng thái r n (tinh th ). Trong bi n thự ồ ấ ể ụ ố ớ ạ ắ ể ế ể
raxemic r n, ngoài l c t ng tác gi a các phân t (-) quay trái, gi a các phân t quay ph i (+) còn cóắ ự ươ ữ ử ữ ử ả
l c t ng tác gi a các phân t (+) và (-). K t qu là tr ng thái r n th ng g p s khác bi t vự ươ ữ ử ế ả ở ạ ắ ườ ặ ự ệ ề
m t s tính ch t gi a bi n th raxemic và ch t đi quang tinh khi t. Có 3 tr ng h p khác bi t sau:ộ ố ấ ữ ế ể ấ ố ế ườ ợ ệ
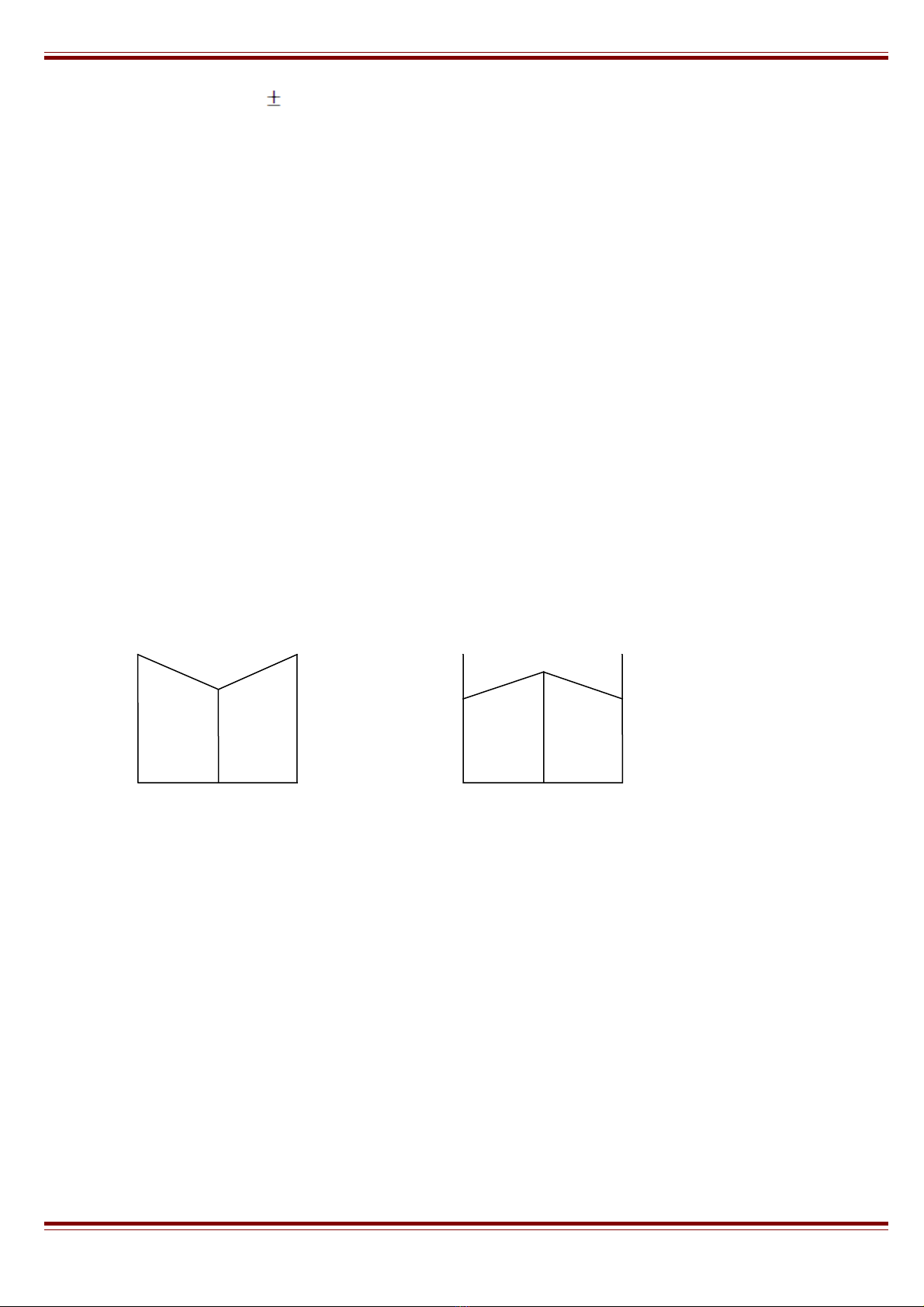
Các h n h p raxemicỗ ợ : là m t h n h p c h c tinh th riêng r c a các ch t đi quang cònộ ỗ ợ ơ ọ ể ẽ ủ ấ ố
g i là conglomerat. Tính ch t c a nó gi ng tính ch t c a các đi quang tinh khi t. Tuy nhiên, nhi tọ ấ ủ ố ấ ủ ố ế ệ
đ nóng ch y c a h n h p raxemic th p h n nhi t đ nóng ch y c a các ch t đi quang tinh khi t,ộ ả ủ ỗ ợ ấ ơ ệ ộ ả ủ ấ ố ế
còn đ tan c a h n h p raxemic l i cao h n. Trên gi n đ nhi t đ nóng ch y, đi m tecti là đi mộ ủ ỗ ợ ạ ơ ả ồ ệ ộ ả ể ơ ể
ng v i nhi t đ nóng ch y th p nh t, đó t l gi a hai ch t đi quang là 50:50.ứ ớ ệ ộ ả ấ ấ ở ỉ ệ ữ ấ ố
Các h p ch t raxemic: ợ ấ Là tr ng h p bi n th raxemic mà ch có m t lo i tinh th đc t oườ ợ ế ể ỉ ộ ạ ể ượ ạ
thành t c hai d ng ch t đi quang có s l ng phân t b ng nhau. H p ch t raxemic là m t lo iừ ả ạ ấ ố ố ượ ử ằ ợ ấ ộ ạ
h p ch t riêng bi t, chúng khác bi t v i các đi quang v tính ch t v t lý nh nhi t đ nóng ch y,ợ ấ ệ ệ ớ ố ề ấ ậ ư ệ ộ ả
đ tan. Nhi t đ nóng ch y c a h p ch t raxemic có th cao h n ho c th p h n các đi quang tinhộ ệ ộ ả ủ ợ ấ ể ơ ặ ấ ơ ố
khi t.ế
H c viên: Nguy n Xuân Phongọ ễ 5
100% (-) 50% (-) 0% (-)
0% (+) 50% (+) 100% (+)
Đ tanộ
0% (+) 50% (+) 100% (+)
100% (-) 0% (-)50% (-)
Nhi t đ nóng ệ ộ
ch yả
Gi n đ nhi t đ nóng ch y và đ tan c a các h n h p raxemicả ồ ệ ộ ả ộ ủ ỗ ợ

![Ứng dụng kỹ thuật trao đổi ion trong điện phân: Bài tiểu luận [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250829/sonphamxuan1808/135x160/97341756442892.jpg)
















![Ô nhiễm môi trường không khí: Bài tiểu luận [Nổi bật/Chi tiết/Phân tích]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251011/kimphuong1001/135x160/76241760173495.jpg)







