
SỞ GIÁO DỤC VÀ ĐÀO TẠO KIỂM TRA CHẤT LƯỢNG HỌC KỲ I
ĐỒNG THÁP Năm học: 2012-2013
Môn thi: TOÁN - Lớp 10
Thời gian: 90 phút (không kể thời gian phát đề)
ĐỀ ĐỀ XUẤT
(Đề gồm có 01 trang).
Đơn vị ra đề: THPT Thanh Bình 1.
I. PHẦN CHUNG CHO TẤT CẢ CÁC HỌC SINH (7.0 điểm )
Câu I: (1,0 điểm) Cho hai tập hợp A={ x x là ước nguyên dương của 20 }, B={ 1; 2; 3; 4; 5; 6 }.
Tìm
A B, A B, A \ B.
Câu II: (2,0 điểm)
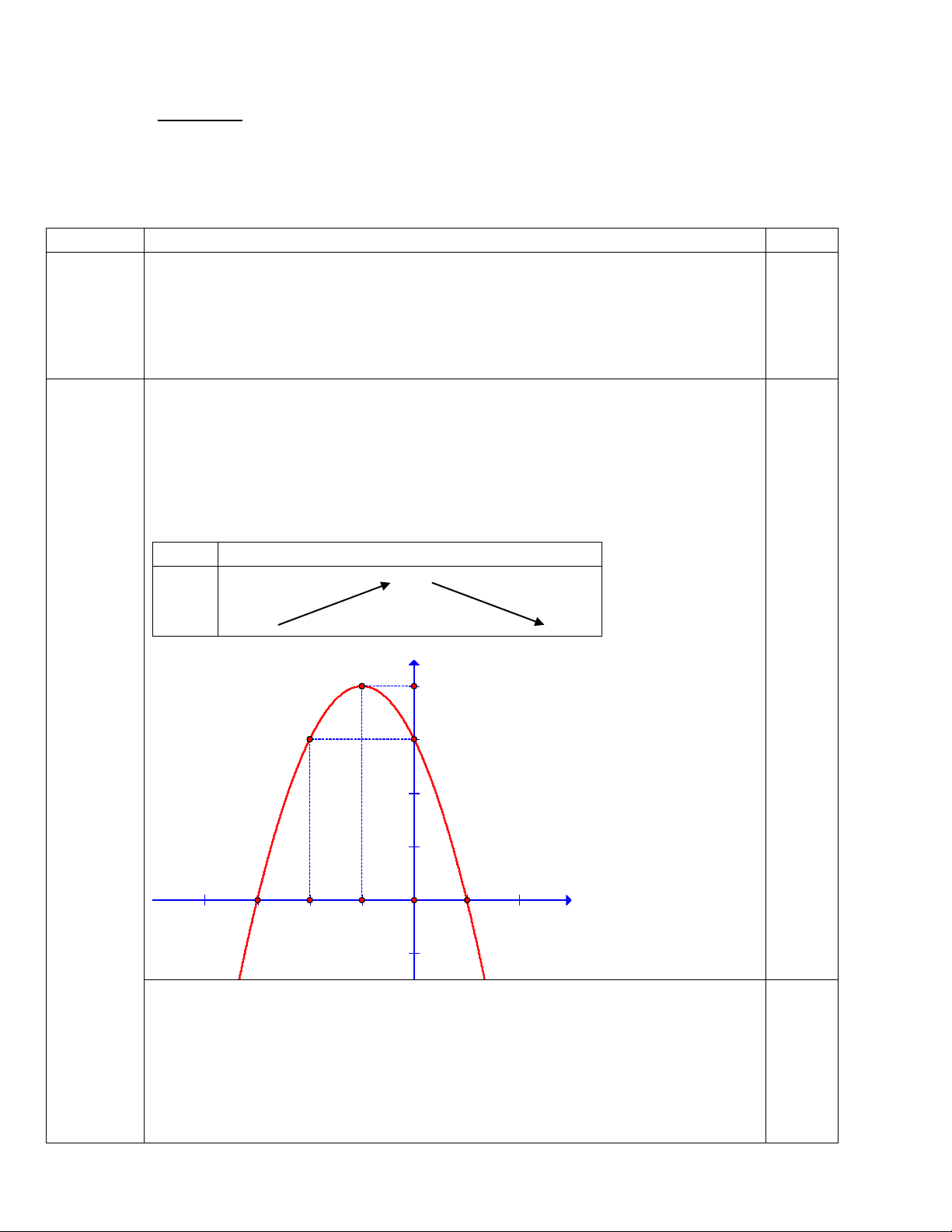
1. Khảo sát và vẽ đồ thị hàm số
3x2xy 2
2. Xác định parabol
22y ax x c
biết parabol đó đi qua A(2; -3), B(1; 4).
Câu III: Giải các phương trình sau:(2,0 điểm)
1. 2( x+3) = x(x-3).
2.
3
x
1
)2x(x
2x
.
Câu IV: (2,0 điểm) Trong mp toạ độ Oxy cho A(1;2); B(–2;6); C(9;8).
1. Tìm
x 2a 3b
biết
a AB
và
b AC
.
2. Tìm toạ độ điểm M trên Oy để B, M, A thẳng hàng.
II. PHẦN RIÊNG ( 3 điểm ).
1. Theo chương trình chuẩn.
Câu Va ( 2 điểm)
1. Giải hệ phương trình
2y2x4
5y4x3
2. Cho a>0; b>0. Chứng minh rằng
ba
a
b
b
a
. Đẳng thức xảy ra khi nào?
Câu VIa (1 điểm). Trong mp Oxy cho A (– 1;3), B(– 3; – 2), C(4;1). Chứng minh
ABC vuông cân
2. Theo chương trình nâng cao.
Câu Vb 2 điểm)
1. Giải hệ phương trình
164yx
2yx
22
2. Cho phương trình: x2 + (m - 1)x – 1 = 0 (1).
Tìm m để phương trình (1) có nghiệm x = –1. Khi đó tìm nghiệm còn lại của phương trình (1).
Câu VIb.(1 điểm) Cho hai điểm M(–3;2) và N(4 ; 3 ). Tìm P trên Ox sao cho tam giác PMN vuông
tại P .
ĐỒNG THÁP Năm học: 2012-2013
Môn thi: TOÁN – Lớp 10
HƯỚNG DẪN CHẤM ĐỀ ĐỀ XUẤT
(Hướng dẫn chấm gồm có 4 trang)
Đơn vị ra đề: THPT Thanh Bình 1
Câu
Nội dung yêu cầu
Điểm
Câu I
(1,0 đ)
- Ta có A={1,2,4,5,10,20};
khi đó:
5;4;2;1BA
20;10;6;5;4;3;2;1BA
20;10B\A
0,25
0,25
0,25
0,25
Câu II
(2,0 đ)
1.
+Tập xác định D=R
+Đỉnh I(-1;4)
+Trục đối xứng x = -1
+Giao với trục tung A(0;3),
+Giao với trục hoành tại B(1;0),B’(-3;0)
+Bảng biến thiên:
x
-
-1 +
y
4
-
-
+ Vẽ đồ thị hàm số
-4 -3 -2 -1 1 2
-1
1
2
3
4
x
y
O
I
0,25
0,25
0,25
0,25
2.
Vì parabol đi qua A (2; -3) ta có: 4a + c = -7
tương tự vì parabol qua B (1; 4) ta có: a+c = 2
nên ta có hệ
4 7 3
25
a c a
a c c
Vậy parabol cần tìm là
2
3 2 5y x x
0,25
0,25
0,25
0,25

Câu III
(2,0 đ)
2
2
1/ 2( 3) ( 3) 2 6 3
1
5 6 0 6
x x x x x x
x
xx x
Vậy phương trình có 2 nghiệm
6x
1x
0, 25
0,5
0,25
2/
Điều kiện :
2 0 2
00
xx
xx
2
22
3
( 2)
2 2( 2) 3 ( 2)
1
3 3 6 0 2
x
x x x
x x x x
x
xx x
So với điều kiện thì nghiệm x = 1 thoả mãn đề bài
Vậy phương trình đã cho có nghiệm duy nhất x=1
0,25
0,25
0,25
0,25
Câu IV
( 2 điểm)
1.
Ta có:
a AB
= ( -3; 4);
b AC
= ( 8; 6);
Suy ra: 2
a
= ( -6; 8)
3
b
= ( 24; 18)
Vậy
x 2a 3b
= ( -30; -10)
0,25
0,25
0,25
0,25
2.
Gọi M ( 0; x)
0y
Ta có
BM
= ( 2; x - 6);
BA
= ( 3; -4 )
Để 3 điểm B, A, M thẳng hàng
4
6x
3
2
3x - 18 = -8 x=
3
10
Vậy M (0;
3
10
)
0,25
0,25
0,25
0,25
Câu Va.
( 2 điểm)
1.
Ta có:
2y2x4
5y4x3
4y4x8
5y4x3
0,25

1x2y
9x11
11
7
y
11
9
x
Vậy hệ pt có 1 nghiệm duy nhất
11
7
;
11
9
0,25
0,25
0,25
2.
Ta có
ba
a
b
b
a
ba
ab
bbaa
)đpcm(0ba0)bab2a(
ab)baba(1
ab
)baba(
ba
ab
)baba)(ba(
ba
ab
ba
2
33
Dấu " =" xảy ra
baba
0,25
0,25
0,25
0,25
Câu VIa
( 1 điểm).
Ta có:
);2;5(AC);5;2(AB
Ta có
0
90AACAB0)2).(5(5.2AC.AB
mặt khác ta có AB =
29)5()2( 22
;
AC =
29)5()2( 22
suy ra AB= AC
Vậy tam giác ABC vuông cân tại A.
0,25
0,25
0,25
0,25

Câu Vb.
( 2 điểm)
8y
10x
10y
8x
8y
10y
2yx
080y2y
2yx
164y4y4y
2yx
164y)2y(
2yx
164yx
2yx
cóTa
222
2222
Vậy hệ pt có 2 nghiêm ( 8; -10) và (10;8)
0,25
0,25
0,25
0,25
2.
Vì pt (1) có một nghiệm x= -1 thế vào pt (1) ta có:
(1)
1m01m01)1)(1m(1 2
mặt khác vì 2 hệ số a và c trái dấu, suy ra pt (1) có 2 nghiệm thỏa
1
m1
a
b
xx 21
với
1x
1m
1
suy ra
1x2
Vậy với m=1 thì pt có 2 nghiệm x=1 và x= -1.
0,25
0,25
0,25
0,25
Câu VIb.
( 1 điểm)
Gọi P(x; 0)
Ox.
Ta có:
)3;x4(PN);2;x3(PM
Vì tam giác PMN vuông tại P
Ta có:
03.2)x4).(x3(0PN.PM
3x
2x
06xx2
Vậy có 2 điểm P(-2; 0) và P(3; 0) thỏa đề bài.
0,25
0,25
0,25
0,25
Lưu ý: Nếu học sinh có cách giải khác mà đúng kết quả thì vẫn được hưởng trọn số điểm.












![Đề thi Tiếng Anh có đáp án [kèm lời giải chi tiết]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250810/duykpmg/135x160/64731754886819.jpg)



