Ngày so n: 30/9/08.ạ
Ngày d y:ạ
Bu i 1. ổ Hàm s .ố
I- M c tiêu.ụ
- C ng c các ki n th c v hàm s .giá tr c a hàm s .t p xác đ nh c a hàmủ ố ế ứ ề ố ị ủ ố ạ ị ủ
s .ố
-S bi n thiên c a hs,hàm s ch n hàm s l .ự ế ủ ố ẵ ố ẻ
Kĩ năng.
- h c sinh thành th o áp d ng các đl,t/c và tm txd, xét s bi n thiên c aọ ạ ụ ự ế ủ
hs.
- Bi t cách xác đ nh hs ch n,l .ế ị ẵ ẻ
T duy,thái đ .ư ộ
- Rèn tính c n th n trong tính toán cho hs.ẩ ậ
- Góp ph n phát tri n t duy ligoic,sáng t o cho hs.ầ ể ư ạ
II- Chu n bẩ ị
1. GV : Chu n b GAẩ ị
2. HS : Ôn t p kĩ các ki n th c c b n nhà.ậ ế ứ ơ ả ở
III- Các ho t đ ng d y và h c.ạ ộ ạ ọ
1. n đ nh l p và ki m tra sĩ s .Ổ ị ớ ể ố
2. Bài gi ng.ả
TG HD c a GvủHD c a HSủN i dung c n đ tộ ầ ạ
GV: Nêu các ví
d cho hs ápụ
d ng.ụ
? TXD.
HS: Lên b ng th c hi n.ả ự ệ
I – HS và GT c a hs t i m tủ ạ ộ
đi m.T p xác đ nh.ể ậ ị
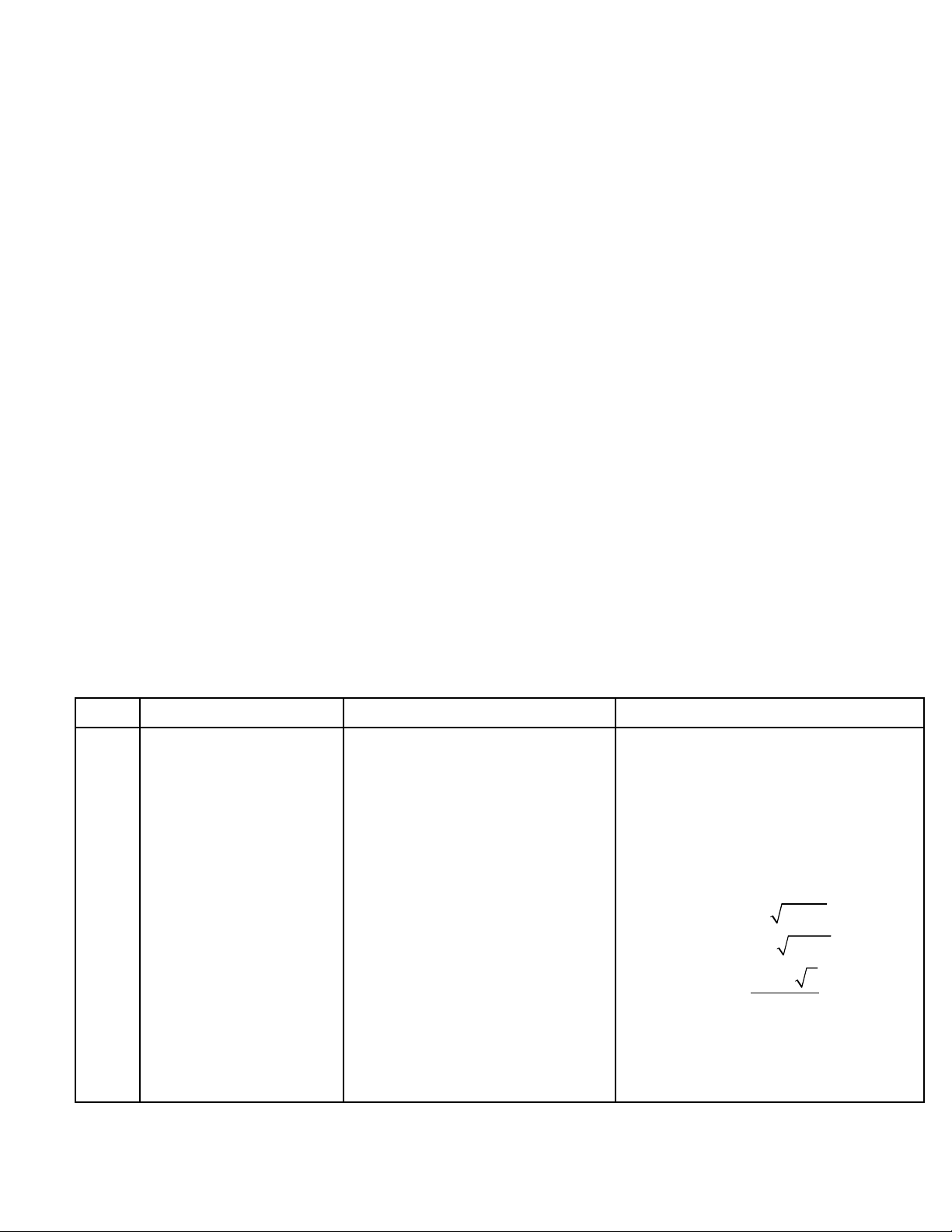
Bài 1.Cho hs.
) 3 2 3
) 2 1 2
12
)2
a y x x
b y x
x x
c y x
= −
= − −
+
=+
Tm t p xác đ nh c a hs. ậ ị ủ
b) tính giá tr c a các hs trênị ủ
l n l t t i : ầ ượ ạ
1

? Đ tính giá trể ị
c ahs t i m tủ ạ ộ
đi m ta th c hi nể ự ệ
nh th nào.ư ế
? Khi nào hs đ cượ
g i là đ ngọ ồ
bi n,ngh ch bi n.ế ị ế
-Nêu cách cm
hàm s đ ngố ồ
bi n, ngh ch bi n.ế ị ế
? Th nào là hsế
ch n, hàm s l .ẵ ố ẻ
HS: tr l i.ả ờ
HS: Lên b ng th c hi n.ả ự ệ
HS: Đ ng t i ch trứ ạ ỗ ả
l i.ờ
HS: N u.ờ
Cho hs y = f(x) xác đ nhị
trên D.
- N u x thu c D, th –xế ộ
thu c D.Và f(x) = f(-x)ộ
x = 0; x= 4 ;x = -2.
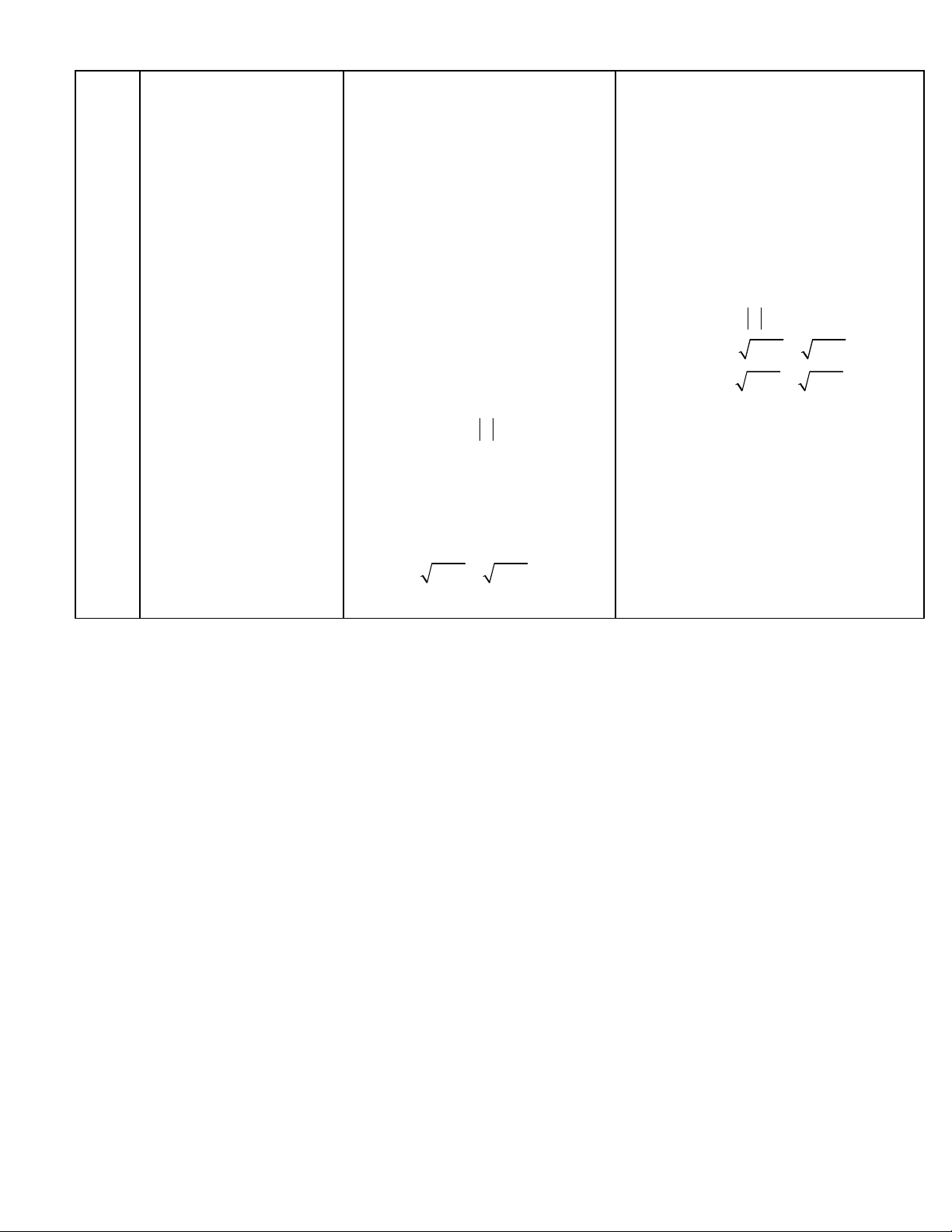
Bài 2:
Tm TXD c a các hs sau. ủ
2
2
1
)1
2 1
)2 1
3 4
)( 2) 4
x
a y x
x
b y x x
x
c y x x
−
=−
+
=− −
+
=− +
Bài 3: bài 2.3 và 2.4 trong
sách bài t p.ậ
II- HS đ ng bi n, ngh chồ ế ị
bi n.ế
Cách cm hs đ ng bi n nb.ồ ế
Bài 4.
Xét s bi n thiên c a các hsự ế ủ
sau.
2
) 4 1a y x x= + +
Trên kho ng ả
( ; 2);( 2 : )−∞ − − +∞
) ;( ; 1),( 1; )
1
x
b y x
= −∞ − − +∞
+
III- HS ch n,hs l .ẵ ẻ
2
? tính f( -x) và so
sánh v i f(x) sauớ
đó k t lu n vế ậ ề
tính ch n,l .ẵ ẻ
hs ch n.ẵ
- N u x thu c D, th –xế ộ
thu c D và f(x) = - f(-x)ộ
hs l .ẻ
HS: a)HS ch n( t ngẵ ổ
c a ba hs ch n)ủ ẵ
b) Hàm s l ( T ng c aố ẻ ổ ủ
hai hs l )ẻ
c) HS l ( tích c a hàmẻ ủ
s l y =x và ố ẻ
hs ch n y = ẵ
x
)
d) T p xác đ nh c a hàmậ ị ủ
s là đo n [-1;1] ,v iố ạ ớ
m i x thu c đo n [ -1;1]ọ ộ ạ
tac c
f(-x)=
1 1 ( )x x f x− + + =
V y hs là ch n.ậ ẵ
Bài 5:
Xét tính ch n ,l c a hs sauẵ ẻ ủ
4 2
3
) 3 3 2
) 2 5
)
) 1 1
) 1 1
a y x x
b y x x
c y x x
d y x x
e y x x
= + −
= −
=
= + − −
= + + −
.
C ng c .ủ ố
- C ng c các kt c b n v a ôn.ủ ố ơ ả ừ
D n d ặ
- V ôn t p các kt đó và lam các bài t p trong sách bài t p.ề ậ ậ ậ
3

Bu i 2ổ:
Ngày so n: 3/10/08.ạ
Ngày d y ạ:
HÀM S B C NH T VÀ B C HAI.Ố Ậ Ấ Ậ
I – M c tiêu.ụ
Ki n th c.ế ứ
C ng c các ki n th c v v đ th hs b c nh t,v trí t ng đ i gi a hai đ ng th ng.ủ ố ế ứ ề ẽ ồ ị ậ ấ ị ươ ố ữ ườ ẳ
-C ng c các kt v hàm s b c hai.đ th hs b c hai.ủ ố ề ố ậ ồ ị ậ
Kĩ năng.
-H c sinh bi t v n d ng linh ho t các kt vào làm bài t p.ọ ế ậ ụ ạ ậ
- Góp ph n rèn kĩ năng v hình cho h c sinh.ầ ẽ ọ
T duy,thái đ .ư ộ
-Góp ph n phát tri n t duy logic,tính c n th n cho hoc sinh.ầ ể ư ẩ ậ
-H c sinh h c t p nghiêm túc,tích c c trao đ i làm bài t p.ọ ọ ậ ự ổ ậ
II - Chu n b :ẩ ị
GV: GA, th c kướ ẻ
HS: Ôn t p các ki n th c c b n v hs b c nh t và b c hai.ậ ế ứ ơ ả ề ậ ấ ậ
III – Các ho t đ ng d y ạ ộ ạ và h c.ọ
1. n đ nh l p và ki m tra sĩ s .ổ ị ớ ể ố
2. Bài gi ng.ả
TG HĐ c a GVủHĐ c a HSủN i dung c n đ tộ ầ ạ
? Nh c l i v cáchắ ạ ề
v đ th hàm b cẽ ồ ị ậ
nh t ấ
? Hai đ ng th ngườ ẳ
c t nhau,songắ
song,trùng nhau khi
nào.
GV: G i h c sinhọ ọ
lên b ng vả ẽ
HS: Tr l i.ả ờ
(d) : y = ax + b
(d’) : y = a’x + b’
. d c t d’ khi a ắ
≠
a’
. d song song v i d’ khiớ
a = a’ và b
≠
b’
. d trùng d’ khi a = a’ và
b = b’.
HS: Lên b ng v .ả ẽ
A- Lí thuy t.ế
1. Hàm s : ố
y = ax +b ( a
≠
0)
- Cách v đ th hàm s .ẽ ồ ị ố
- V trí t ng đ i gi a haiị ươ ố ữ
đ ng th ng.ườ ẳ
Bài 1:
V đ th c a các hàm s sau.ẽ ồ ị ủ ố
) 2 3
1
) 1
2
a y x
b y x
= −
= − +
Bài 2: (2.15sbt)
Cho hàm s .ố
4

? Đ đ ng th ngể ườ ẳ
đi qua g c to đ taố ạ ộ
c n có đi u gì.ầ ề
?: a và b tho mãnả
h ph ng trìnhệ ươ
nào.
? Kh o sát s bi nả ự ế
thiên hàm b c hai.ậ
? Nh c l i v cáchắ ạ ề
v đ th hàm sẽ ồ ị ố
b c hai.ậ
HS:
a) k = 0
b) 3 = -2(-2) + k(
-2+1)
⇔
k = 1
c) k = 2 +
2
HS:
a) trên đ ng th ng ườ ẳ
y = 2x +5, đi m cóể
hoành đ -2 làộ
A ( -2;1).trên đ ngườ
th ng y = -3x +4 ,đi mẳ ể
có tung đ b ng -2 là ộ ằ
B( 2;-2).
V y đ ng th ng c nậ ườ ẳ ầ
tìm đI qua 2 đi m A vàể
B,v y a và b tho mãnậ ả
h .ệ
3
2 1 4
2 2 1
2
a
a b
a b b
= −
− + =
⇒
+ = −
= −
b)
1
2
15
7
a
b
=
=
4)
a) B(x0;-y0)
HS: Nêu các b c nhướ ư
trong sách.
2 ( 1)y x k x= − + +
tìm k sao cho đ th hàm s .ồ ị ố
a) Đi qua g c to đ .ố ạ ộ
b) Đi qua đi m M(-2;3)ể
c) Song song v i đ ng th ng ớ ườ ẳ
y =
2x
Bài 3: ( 2.18sbt)
Trong các tr ng h p sau ,xácườ ợ
d nh a và b sao cho đ ng th ngị ườ ẳ
y = ax +b
a)C t đ ng th ng y = 2x +5 t iắ ườ ẳ ạ
đi m có hoành đ b ng -2 vàể ộ ằ
c t đ ng th ng y = -3x +4 t iắ ườ ẳ ạ
đi m có tung đ b ng -2.ể ộ ằ
b)Song song v i đ ng th ng yớ ườ ẳ
=
1
2x
và đi qua giao đi m c aể ủ
hai đ ng th ng y =ườ ẳ
11; 3 5
2x y x− + = +
Bài 4: (2.19 sbt)
a)Cho đi m A(xể0;y0) .Hãy xác
đ nh to đ c a đi m B,biét Bị ạ ộ ủ ể
đ i x ng v i A qua tr c hoành.ố ứ ớ ụ
b)Ch ng minh r ng hai đ ngứ ằ ườ
th ng y = x -2 ; ẳ
y= 2 – x đ i x ng v i nhauố ứ ớ
qua tr c hoành.ụ
c)Tìm bi u th c xác đ nh hàm sể ứ ị ố
y = f(x) ,bi t r ng đ th c a nóế ằ ồ ị ủ
là đ ng th ng đ i x ng v iườ ẳ ố ứ ớ
đ ng th ng y = -2x +3.ườ ẳ
B – Hàm s b c hai.ố ậ
Bài 5: Kh o sát s bi n thiên vàả ự ế
v đ th hàm s .ẽ ồ ị ố
2
2
) 1
) 2 2
a y x x
b y x x
= + +
= − + −
5


























