bé gi¸o dôc vµ ®µo t¹o
--------------------
kú thi tèt nghiÖp trung häc phæ th«ng
n¨m häc 2002 – 2003
-------------------
h−íng dÉn chÊm §Ò chÝnh thøc
m«n to¸n
* B¶n h−íng dÉn chÊm thi nµy cã 4 trang *
I. C¸c chó ý khi chÊm thi
1) H−íng dÉn chÊm thi (HDCT) nµy nªu biÓu ®iÓm chÊm thi t−¬ng øng víi ®¸p ¸n nªu d−íi ®©y.
2) NÕu thÝ sinh cã c¸ch gi¶i ®óng, c¸ch gi¶i kh¸c víi ®¸p ¸n, th× ng−êi chÊm cho ®iÓm theo sè
®iÓm qui ®Þnh dµnh cho c©u ( hay phÇn
♦
) ®ã.
3) ViÖc vËn dông HDCT chi tiÕt tíi 0,25 ®iÓm ph¶i thèng nhÊt trong tÊt c¶ c¸c tæ chÊm thi m«n
To¸n cña Héi ®ång.
4) Sau khi céng ®iÓm toµn bµi míi lµm trßn ®iÓm m«n thi theo qui ®Þnh chung.
II. §¸p ¸n vµ c¸ch cho ®iÓm
Bµi 1 (3 ®iÓm).
1. (2, 5 ®iÓm)
- TËp x¸c ®Þnh R \ { 2}. (0, 25 ®iÓm)
- Sù biÕn thiªn:
a) ChiÒu biÕn thiªn:
♦
2
1
2−
−+−=
x
xy , y ' = 2
2
)2(
34
−
−+−
x
xx ,
=
=
⇔= 3
1
0' x
x
y
y’< 0 víi ∀
(
)
(
)
∞∪∞−∈ ;31;x: hµm sè nghÞch biÕn trªn c¸c kho¶ng
(
)( )
+∞∞− ;3,1; .
y’ > 0 víi ∀
()
2;1∈x∪(2; 3): hµm sè ®ång biÕn trªn c¸c kho¶ng (1; 2), (2; 3).
(0, 75 ®iÓm)
b) Cùc trÞ:
♦
Hµm sè cã hai cùc trÞ: cùc tiÓu yCT = y(1) = 2 , cùc ®¹i yC§ = y(3) = - 2.
(0, 25 ®iÓm)
c) Giíi h¹n:
♦
.
2
54
2
2
lim
2
lim,
2
54
2
2
lim
2
lim ∞−=
−
−+−
+
→
=
+
→
∞+=
−
−+−
−
→
=
−
→x
xx
x
y
x
x
xx
x
y
x
§å thÞ cã
tiÖm cËn ®øng x = - 2.
♦
0)
2
1
(lim)]2([lim =
−
−
∞→
=+−−
∞→ x
x
xy
x. §å thÞ cã tiÖm cËn xiªn y = - x + 2.
(0, 25 ®iÓm)
(0, 25 ®iÓm)
d) B¶ng biÕn thiªn:
(0, 25 ®iÓm)
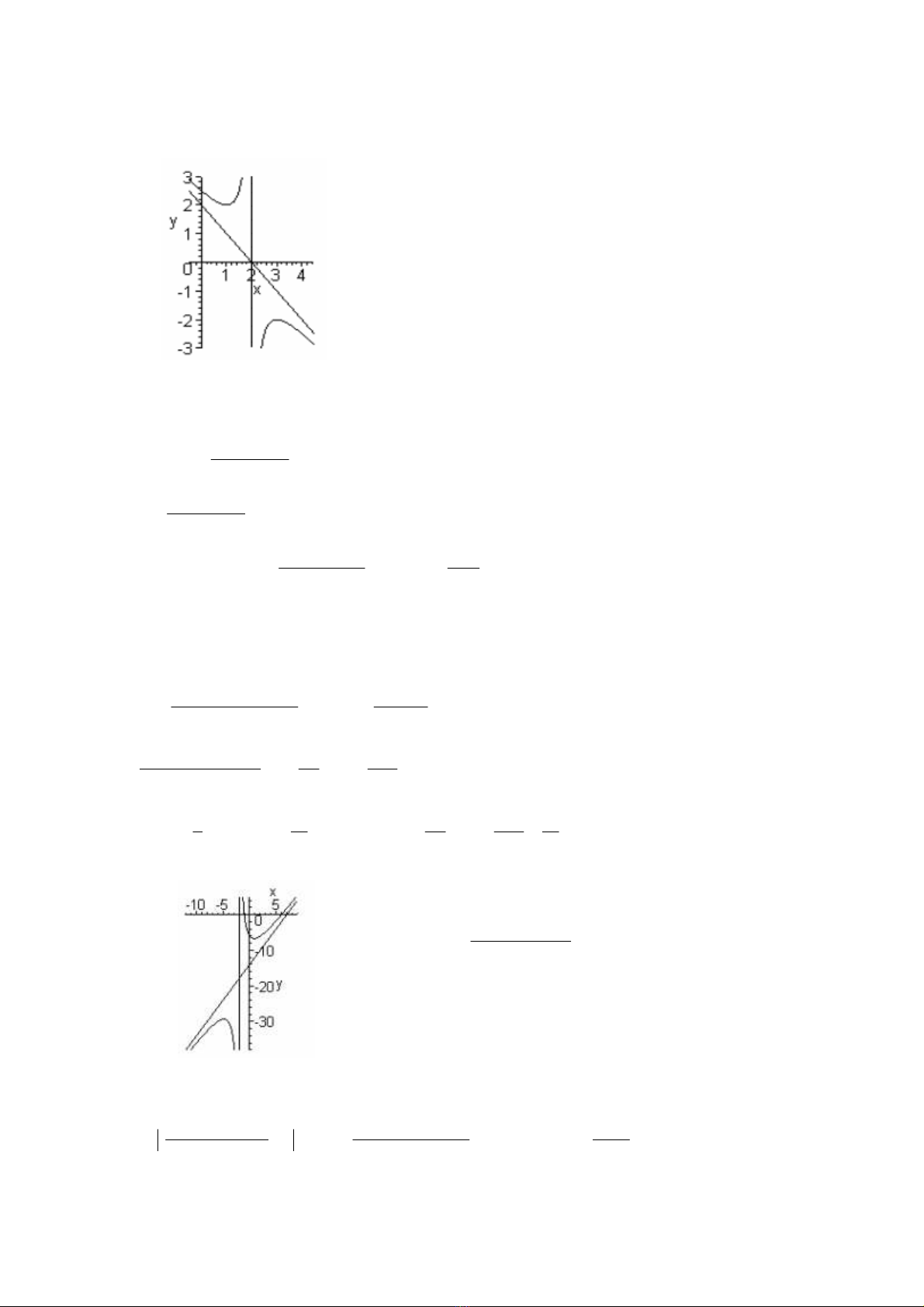
- §å thÞ:
x
∞
+
∞− 321
y’ - 0 + + 0 -
y + ∞ + ∞ - 2
C§
CT
2 - -∞ - ∞
H−íng dÉn chÊm thi TNTHPT n¨m 2003: ®Ò chÝnh thøc
2
(0, 50 ®iÓm)
2. ( 0, 5 ®iÓm)
♦
2
16
2
2−+
−−
++−= mx
mm
xy , ®å thÞ cã tiÖm cËn ®øng lµ x = 2 khi vµ chØ khi ∞=
→y
x2
lim
⇔∞=
−+
−−
→2
16
2
2
lim mx
mm
x. Qua giíi h¹n cã 2 + m – 2 = 0 hay m = 0.
♦
Víi m = 0 ta cã 2
1
2
2
54
2
−
−+−=
−
−+−
=
x
x
x
xx
y; nªn ®å thÞ hµm sè cã tiÖm cËn
xiªn lµ y = - x +2.
VËy gi¸ trÞ cÇn t×m cña m lµ m = 0.
(0, 25 ®iÓm)
(0, 25 ®iÓm)
Bµi 2 (2 ®iÓm )
1. (1 ®iÓm)
♦
2
2
23
)1(
2
1
)1(
133
)(
+
−+=
+
−++
=
x
x
x
xxx
xf
;
1
2
2
2
2
)1(
13
2
3
3
C
x
x
x
dx
x
xxx +
+
++=⇒ ∫+
−++
♦
V× 3
1
)1( =Fnªn 6
13
−=C. Do ®ã 6
13
1
2
2
)(
2−
+
++= x
x
x
xF .
(0, 75 ®iÓm)
(0, 25 ®iÓm)
2. ( 1 ®iÓm)
♦
DiÖn tÝch h×nh ph¼ng S cÇn t×m
∫∫∫
−
−− +
−−
+
++−
−
+
−− ===
6
1
6
1
2
6
1
2
)
2
16
214(
2
12102
0
2
12102 dx
x
xdx
x
xx
dx
x
xx
S
(0, 25 ®iÓm)
VÏ ®óng d¹ng ®å thÞ :
+ Giao víi Oy: t¹i ®iÓm
(0; 2,5)
+ §å thÞ cã t©m ®èi xøng t¹i
®iÓm ( 2 ; 0).
+ §å thÞ cã hai tiÖm cËn:
x = 2 vµ y = - x + 2.
♦
Gi¶i ph−¬ng tr×nh:
2
12102 2
+
−−
x
xx = 0
ta t×m ®−îc c¸c cËn lÊ
y
tÝch
p
h©n
lµ: - 1 vµ 6.

H−íng dÉn chÊm thi TNTHPT n¨m 2003: ®Ò chÝnh thøc
3
.8ln1663)2ln1614( 6
1
2−=+−−= −
xxx
(0, 75 ®iÓm)
Bµi 3 (1, 5 ®iÓm)
1. (1 ®iÓm).
♦ Gi¶ sö ®iÓm M ë gãc phÇn t− thø nhÊt vµ M = (x; y). Khi ®ã theo ®Çu bµi ta cã
c¸c hÖ thøc: c¸c b¸n kÝnh qua tiªu 1
MF = a + ex = 15, 2
MF = a - ex = 9, kho¶ng
c¸ch gi÷a c¸c ®−êng chuÈn: 2 . e
a = 36. VËy a = 12, e = 3
2, x = 2
9.
♦ V× c = a.e = 8 vµ cã b2= a2- c2= 80 nªn ph−¬ng tr×nh chÝnh t¾c cña elÝp (E) lµ
1
80
2
144
2
=+ yx
(0, 75 ®iÓm)
(0, 25 ®iÓm)
2. (0, 5 ®iÓm).
♦ TiÕp tuyÕn víi elÝp (E) t¹i ®iÓm M( 2
9; 2
115 ) lµ 3211 =+ yx .
♦ Trªn elÝp (E) cßn 3 ®iÓm cã to¹ ®é lµ (- 2
9; 2
115 ), ( 2
9; - 2
115 ), (- 2
9; - 2
115 )
còng cã c¸c b¸n kÝnh qua tiªu lµ 9 vµ 15. Do ®ã ta cßn cã 3 ph−¬ng tr×nh tiÕp tuyÕn
víi elÝp (E) t¹i c¸c ®iÓm (t−¬ng øng) ®ã lµ : - 3211 =+ yx , 3211 =− yx ,
3211 −=+ yx
(0, 25 ®iÓm)
(0, 25 ®iÓm)
Bµi 4 (2, 5 ®iÓm)
1. (1 ®iÓm)
♦Theo ®Çu bµi ta cã A= (2; 4; -1), B = (1; 4; -1), C = (2; 4; 3), D = (2; 2; -1). Do ®ã:
ADABADAB
ADACADAC
ACABACAB
⊥⇒=+−+−=
→→
⊥⇒=+−+=
→→
⊥⇒=++−=
→→
00.0)2.(00).1(.
00.4)2.(00.0.
04.00.00).1(.
♦ ThÓ tÝch khèi tø diÖn ABCD tÝnh theo c«ng thøc
VABCD =→→→
ADACAB ].,[
6
1= 3
4 (do )0;4;0(],[ =
→→
ACAB )
(0, 75 ®iÓm)
(0,2 5 ®iÓm)
2. (0, 75 ®iÓm)
♦ §−êng th¼ng CD n»m trªn mÆt ph¼ng (ACD) mµ mÆt ph¼ng (ACD) ⊥ AB nªn
®−êng vu«ng gãc chung ∆ cña AB vµ CD lµ ®−êng th¼ng qua A vµ vu«ng gãc víi CD.
VËy ®−êng th¼ng ∆ cã vect¬ chØ ph−¬ng )1;2;0(],[
2
1−=
→→
=
→
CDABu vµ ph−¬ng tr×nh
tham sè lµ:
+−=
−=
=
tz
ty
x
1
24
2
(0, 50 ®iÓm)
♦ MÆt ph¼ng (ABD) cã vect¬ ph¸p tuyÕn [=
→
n
→
AB ,→
AD ] = (0; 0; 2). VËy gãc nhän
ϕ gi÷a ∆ vµ mÆt ph¼ng (ABD) x¸c ®Þnh bëi biÓu thøc:

H−íng dÉn chÊm thi TNTHPT n¨m 2003: ®Ò chÝnh thøc
4
sin ϕ = →→
→→
un
un
.
.
5
5
52
2
1)2(.2
1.2)2.(00.0
2
2
2
==
+−
+−+
=
(0, 25 ®iÓm)
3. (0, 75 ®iÓm)
♦ Ph−¬ng tr×nh mÆt cÇu (S) cã d¹ng:
0222
222 =++++++ dczbyaxzyx
Bèn ®iÓm A, B, C, D n»m trªn mÆt cÇu nªn cã to¹ ®é tho¶ m·n ph−¬ng tr×nh trªn.
Do ®ã c¸c hÖ sè a, b, c, d lµ nghiÖm cña hÖ ph−¬ng tr×nh sau:
∈=+−++
∈=++++
∈=+−++
∈=+−++
)(02449
)(068429
)(028218
)(028421
SDdcba
SCdcba
SBdcba
SAdcba
Gi¶i hÖ nµy cã a = 2
3
−, b = -3, c = - 1, d = 7. Do ®ã ph−¬ng tr×nh mÆt cÇu (S) lµ:
07263
222 =+−−−++ zyxzyx .
(0, 50 ®iÓm)
♦ MÆt cÇu (S) cã t©m K = ( 2
3; 3; 1) vµ b¸n kÝnh R =
2
21 ; ph−¬ng tr×nh cña mÆt
ph¼ng (ABD) lµ: z + 1 = 0. Ph−¬ng tr×nh mÆt ph¼ng song song víi mÆt ph¼ng (ABD)
cã d¹ng z + d = 0. MÆt ph¼ng ®ã lµ tiÕp diÖn cña mÆt cÇu (S) khi vµ chØ khi kho¶ng
c¸ch tõ t©m K ®Õn mÆt ph¼ng ®ã b»ng R:
2
221
2
,
2
221
1
2
21
2
1
2
0
2
0
1.1 +
−=
−
=⇒=
++
+dd
d.
VËy cã hai tiÕp diÖn cña mÆt cÇu (S) cÇn t×m lµ:
(α1): z + 2
221 − = 0
(α2): z
2
221 +
− = 0
(0, 25 ®iÓm)
Bµi 5 (1 ®iÓm).
♦ HÖ thøc 2:5:6
1
:
1
:
1=
−
+
+C
y
x
C
y
x
C
y
xvíi x vµ
y
lµ c¸c sè n
g
u
y
ªn d−¬n
g
mµ
2 ≤ y+1 ≤ x cho hÖ ph−¬ng tr×nh sau:
−
=
+
+
=
+
2
1y x
C
6
y
1x
C
5
1y x
C
6
y
1x
C
♦ Gi¶i hÖ:
=
=
⇔
=
+
+
=
−+−
+
⇔
+−−
=
−+
+
−−+
=
−+
+
3
8
26
1
)1(5
1
)1)((6
1
)!1()!1(2
!
)!1(!6
)!1(
)!1()!1(5
!
)!1(!6
)!1(
1y
x
y
x
yyxyx
x
yxy
x
yxy
x
yxy
x
yxy
x
(0, 50 ®iÓm)
(0, 50 ®iÓm)
--------- HÕT ---------












![Đề thi tiếng Anh tốt nghiệp THPT 2025 (Chính thức) kèm đáp án [mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250627/laphong0906/135x160/9121751018473.jpg)



