
LUYỆN TẬP 2
I.MỤC TIÊU
+Kiến thức: Củng cố hai trường hợp bằng nhau của hai tam giác cạnh - cạnh -
cạnh và cạnh - góc - cạnh.
+Kỹ năng: Rèn kĩ năng áp dụng trường hợp bằng nhau c.g.c để chỉ ra hai tam giác
bằng nhau từ đó chỉ ra 2 cạnh, 2 góc tương ứng bằng nhau. Rèn kĩ năng vẽ hình.
chứng minh.
+Thái độ: Có ý thức vận dụng kiến thức đã học vào việc giải bài tập.
II.CHUẨN BỊ
1.Giáo viên.
-Thước thẳng, thước đo góc, com pa, êke, bảng phụ
2.Học sinh.
-Thước thẳng, thước đo góc, com pa, êke
III.CÁC HOẠT ĐỘNG DẠY - HỌC

1.Ổn định tổ chức.
-Kiểm tra sĩ số : 7A: /37. Vắng:
....................................................................................................................................
....
7B: /38. Vắng:
....................................................................................................................................
....
2.Kiểm tra.
HS1.Phát biểu trường hợp bằng nhau
c.c.c và c.g.c của hai tam giác?
Kiểm tra quá trình làm bài tập của 5-7
học sinh
GV nhận xét, cho điểm HS.
HS1.Lên bảng thực hiện.
HS dưới lớp nhận xét, bổ sung.
3.Bài mới
HOẠT ĐỘNG CỦA GIÁO VIÊN HOẠT ĐỘNG CỦA HỌC SINH
Hoạt động 1. Chữa bài tập về nhà.
GV yêu cầu học sinh đọc kĩ đầu bài.
-Tại sao không thể áp dụng trường
hợp cạnh - góc - cạnh để kết luận
ABC =
A'BC ?
-Hai tam giác bằng nhau theo trường
I.Chữa bài tập.
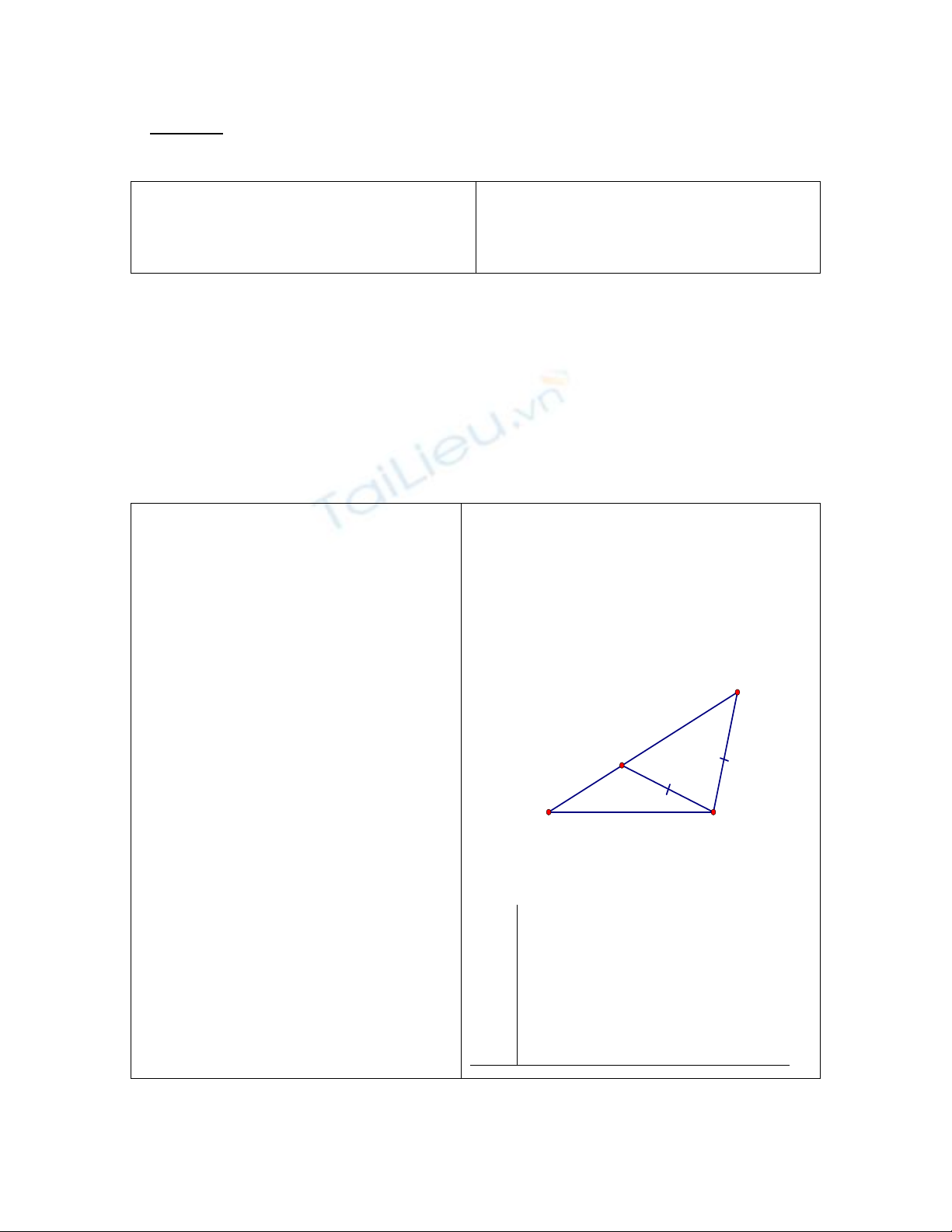
Bài 30 SGK.Tr.120)
2
2
3
300
BC
A'
A
GT
ABC và
A'BC
BC = 3cm, CA = CA' = 2cm
hợp c.g.c thì cặp góc bằng nhau có
đặc điểm gì?
-Hai tam giác trên có những cặp cạnh
nào bằng nhau ?
-Góc xen giữa hai cặp cạnh này có
bằng nhau không ?
0
' 30
ABC A BC
KL
ABC
A'BC
Chứng minh
Góc ABC không xen giữa AC, BC,
'
A BC
không xen giữa BC, CA'
Do đó không thể sử dụng trường hợp
cạnh –góc - cạnh để kết luận
ABC =
A'BC được.
Hoạt động 2. Luyện tập.
-Một đường thẳng là trung trực của AB thì
nó thoả mãn các điều kiện nào?
II. Luyện tập.
Bài 31 SGK.Tr.120.
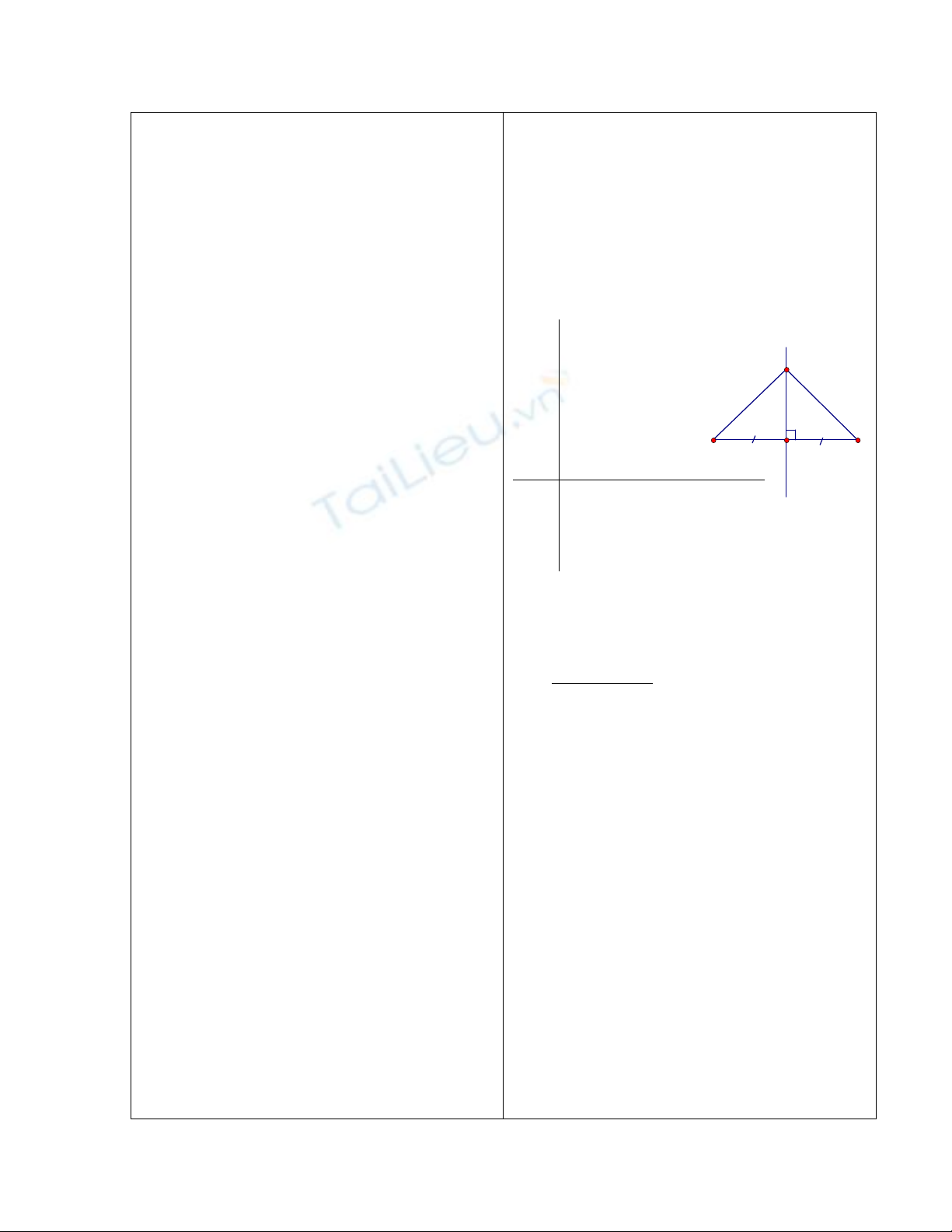
Yêu cầu học sinh vẽ hình
1. Vẽ trung trực của AB
2. Lấy M thuộc trung trực
(TH1: M
I, TH2: M
I)
Hướng dẫn:
MA = MB
MAI =
MBI
IA = IB,
AIM BIM
, MI chung
GT GT
HS: + Đi qua trung điểm của AB
+ Vuông góc với AB tại trung điểm.
Vẽ hình ghi GT, KL
GT
IA = IB, d
AB tại I
M
d
KL
So sánh MA , MB
Chứng minh
*TH1: M
I
AM = MB
*TH2: M
I:
Xét
AIM,
BIM có: AI = IB (GT)
AIM BIM
(GT), MI chung.
d
IA B
M
















