Robotics
ng d ng Maple trong tính toán rô b tỨ ụ ố
1. X lý file và th hi n s li uử ể ệ ố ệ
-T o 1 th m c (folder) đ làm vi cạ ư ụ ể ệ
-L u 1 file maple (ví d : xulyfile.mw) vào th m c trênư ụ ư ụ
-Ch ng trình ch y s t đ ng t o file trong th m c nàyươ ạ ẽ ự ộ ạ ư ụ
-D li u th ng l u tr d ng file text (.txt) d đ c và x lý, s li u l u đ n gi n d ng ma tr n s ,ữ ệ ườ ư ữ ạ ễ ọ ử ố ệ ư ơ ả ạ ậ ố
l y d li u ra d ng ma tr n s và x lý ma tr n s này.ấ ữ ệ ạ ậ ố ử ậ ố
1. X lý fileử
-M file d li u, vi t d li u, l u d li u.ở ữ ệ ế ữ ệ ư ữ ệ
-M file d li u, đ c d li u (l y d li u t file l u tr )ở ữ ệ ọ ữ ệ ấ ữ ệ ừ ư ữ
1.1.X lý file văn b nử ả
Nguyên t c: T o file m i (m file)->Ghi d li u lên file->Đóng fileắ ạ ớ ở ữ ệ
L nh m file:ệ ở fopen
C th : HEPLụ ể
fopen(name, mode)
fopen(name, mode, type)
Vi t lên file:ế fprintf
C th : HEPLụ ể
Đóng file: close
Ví d :ụ
>fh := fopen("xuly.txt", WRITE)
>fprintf(fh, "x=%d,y=%d", 1, 2)
>fclose(fh)
1.2.X lý file d ng sử ạ ố
Nguyên t c: T o file m i (m file)->Ghi d li u lên file->Đóng fileắ ạ ớ ở ữ ệ
L nh m file:ệ ở fopen
Vi t d li u d ng s lên file:ế ữ ệ ạ ố writedata
L nh đ c d li u:ệ ọ ữ ệ readdata
L nh đóng fileệ: fclose
Ví d vi t d li u:ụ ế ữ ệ
>A := matrix([[1, 2, 3, 90], [6, 8, 80, 56], [1, 5, 8, 3]])
>fh := fopen("matrandulieu.txt", WRITE)
>writedata(fh, A, float)
>fclose(fh)
Mu n m và l u file vào th m c khác:ố ở ư ư ụ
fh := fopen("D:/study/fileMOI.txt", WRITE)
fclose(fh)
Ví d đ c d li u:ụ ọ ữ ệ
> fh := fopen("matrandulieu.txt", READ);
0
> datalayra := readdata(fh, float, 4);
[[1., 2., 3., 90.], [6., 8., 80., 56.], [1., 5., 8., 3.]]
> datalayra;
[[1., 2., 3., 90.], [6., 8., 80., 56.], [1., 5., 8., 3.]]
> datalayra[1, 1];
1.
> fclose(fh);
2. Hi n th s li u d ng sể ị ố ệ ạ ố
2.1 T o file d li uạ ữ ệ
Ví d :ụ
> matran := matrix(100, 2);
> for i from 1to 100 by 1 do
matran[i, 1] := i:
matran[i, 2] := i^2:
end do;
> fh := fopen("thehiensolieu.txt", WRITE);
0
> writedata(fh, matran, integer);
> fclose(fh);
2.2 Th hi n d li uể ệ ữ ệ
- đ c file: readdataọ
fh := fopen("thehiensolieu.txt", READ)
-L u thành ma tr nư ậ
matransolieu := readdata(fh, integer, 2)
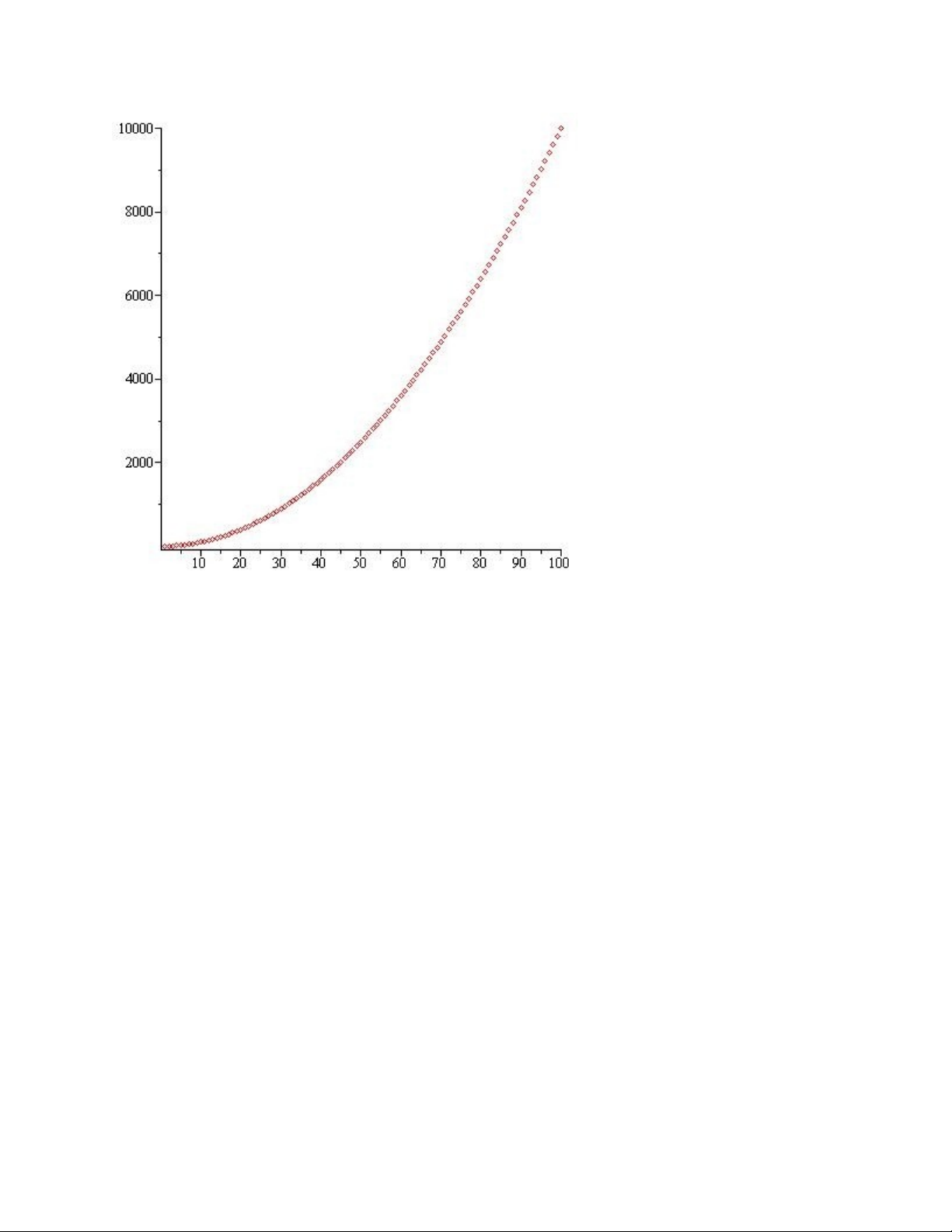
-V đ th các đi m riêng rẽ ồ ị ể ẽ
> points := {seq([matransolieu[i, 1], matransolieu[i, 2]], i = 1 .. 100)};
> pointplot(points, color = red, thickness = 3);
II. H NG D N GI I PH NG TRÌNH Đ NG H C B NG MAPLEƯỚ Ẫ Ả ƯƠ Ộ Ọ Ằ
1. Khai báo th vi n s d ngư ệ ử ụ
with(linalg);
with(VectorCalculus);
with(LinearAlgebra);
with(plots);
with(plottools):
2. Thi t l p ph ng trình đ ng h cế ậ ươ ộ ọ
-B ng cách gán ma tr n tr ng thái khâu thao tác A theo t a đ thao tácằ ậ ạ ọ ộ
p=[xE,yE,zE,rotx,roty,rotz]T và ma tr n tr ng thái khâu thao tác A theo c u trúc đ ngậ ạ ấ ộ
h c q=[q1,q2,zE,…,qn]T. Ta đ c ph ng trình đ ng h c.ọ ượ ươ ộ ọ
-Sau đây là 1 ví d ph ng trình đ ng h c:ụ ươ ộ ọ
f1:=0.28-(.61*(cos(q2)*cos(q3)-sin(q2)*sin(q3)))*cos(q4)*sin(q5)+(.61*(-cos(q2)*sin(q3)-
sin(q2)*cos(q3)))*cos(q5)-.86*cos(q2)*sin(q3)-.86*sin(q2)*cos(q3)+.7*cos(q2)-xE:
f2:=-0.61*(cos(q2)*sin(q3)+sin(q2)*cos(q3)))*cos(q4)*sin(q5)+(.61*(cos(q2)*cos(q3)-
sin(q2)*sin(q3)))*cos(q5)-.86*sin(q2)*sin(q3)+.86*cos(q2)*cos(q3)+.7*sin(q2)-yE:
f3:=-0.61*sin(q4)*sin(q5)+q1-zE:
f4:=-((cos(q2)*cos(q3)-sin(q2)*sin(q3))*cos(q4)*cos(q5)+(-cos(q2)*sin(q3)-
sin(q2)*cos(q3))*sin(q5))*sin(q6)-(cos(q2)*cos(q3)-
sin(q2)*sin(q3))*sin(q4)*cos(q6)+cos(roty)*sin(rotz):
f5:=(cos(q2)*sin(q3)+sin(q2)*cos(q3))*cos(q4)*sin(q5)-(cos(q2)*cos(q3)-
sin(q2)*sin(q3))*cos(q5)+sin(rotx)*cos(roty):
f6:=sin(q4)*cos(q5)*cos(q6)+cos(q4)*sin(q6)+cos(rotx)*sin(roty)*cos(rotz)-sin(rotx)*sin(rotz):
f := [f1, f2, f3, f4, f5, f6]:
3. Gi i bài toán thu nả ậ
3.1. Đ u vào bài toán thu nầ ậ
- Cho tr c q=[q1,q2,q3,…,qn]T (chú ý sv cho ph i phù h p v i c u hình)ướ ả ợ ớ ấ
Ví d :ụ
q1:=1+0.8*sin(Pi/4*t):
q2:=-0.5+0.2*sin(Pi/5*t):
q3:=0.3-0.5*sin(Pi/6*t):
q4:=0.2+0.3*sin(Pi/3*t):
q5:=-0.4-0.3*sin(Pi/4*t):
q6:=0.1+0.4*sin(Pi/5*t):
q := [q1, q2, q3, q4, q5, q6];
-Bi n (đ u ra bài toán thu n)ế ầ ậ
unknow := [xE, yE, zE, rotx, roty, rotz];
3.2. Cách gi iả
- Tìm nghi m đ uệ ầ unknowinit
qinit := evalf(subs(t = 0, q));
f0 := evalf(subs(t = 0, f));
unknow0 := solve(f0, unknow);
assign(unknow0[10]);
unknowinit := [xE, yE, zE, rotx, roty, rotz];
unassign('xE', 'yE', 'zE', 'rotx', 'roty', 'rotz');
-Dùng thu t gi i NewtonRaphson đ gi iậ ả ể ả
read "NewtonRS.txt";
L := 100:
nghiemthuan := matrix(L, 6):
nghiemthuan[1, 1] := unknowinit[1]:
nghiemthuan[1, 2] := unknowinit[2]:
nghiemthuan[1, 3] := unknowinit[3]:
nghiemthuan[1, 4] := unknowinit[4]:
nghiemthuan[1, 5] := unknowinit[5]:
nghiemthuan[1, 6] := unknowinit[6]:
for i from 1 to L-1 by 1 do
Eqts := subs(t = VectorCalculus[`*`](.1, i), f):
jaco := jacobian(f, unknow):
y := Newton_Raphson(Eqts, jaco, unknow, unknowinit):
nghiemthuan[i+1, 1] := evalf(y[1]):
nghiemthuan[i+1, 2] := evalf(y[2]):
nghiemthuan[i+1, 3] := evalf(y[3]):
nghiemthuan[i+1, 4] := evalf(y[4]):
nghiemthuan[i+1, 5] := evalf(y[5]):
nghiemthuan[i+1, 6] := evalf(y[6]):
end do:
-L u k t qu bài toán thu n (l u thành c t” xE yE zE rotx roty rotz”)vàoư ế ả ậ ư ộ
file nghiembaitoanthuan.txt
fh := fopen("nghiembaitoanthuan.txt", WRITE);
writedata(fh, nghiemthuan, float);
fclose(fh);
-Đ c d li uọ ữ ệ
fh := fopen("nghiembaitoanthuan.txt", READ);
vethuan := readdata(fh, float, 6);
fclose(fh);
-L p t a đ đi m tác đ ng cu i theo th i gian tậ ọ ộ ể ộ ố ờ
pointxE := [seq(0.1*i, vethuan[i, 1]], i = 1 .. 100)]:
pointyE := [seq(0.1*i, vethuan[i, 2]], i = 1 .. 100)]:
pointzE := [seq(0.1*i, vethuan[i, 3]], i = 1 .. 100)]:
-V t a đ đi m tác đ ng cu i (thành ph n t a đ và t a đ 3D)ẽ ọ ộ ể ộ ố ầ ọ ộ ọ ộ
point1 := pointplot(pointxE, color = red, legend = "xE");
point2 := pointplot(pointyE, color = green, legend = "yE");
point3 := pointplot(pointzE, color = blue, legend = "zE");
display({point1, point2, point3});