
1
I) DNG ĐI S CA S PHC
Dng 1) Bài toán liên quan ñn bin ñi s phc
Ví d 1) Tìm s nguyên x, y sao cho s phc z=x+yi tho mãn
3
18 26
z i
= +
Gii:
3
18 26
z i
= +
( )
( ) ( )
3 2
32 3 3 2
2 3
3 18
18 26 18 3 26 3
3 26
x xy
x yi i
x y y x xy
x y y
− =
⇔ + = + ⇔ ⇔ − = −
− =
Gi
i ph
ươ
ng trình b
ng cách
ñ
t y=tx ta
ñư
c
13, 1
3
t x y=⇒= = . Vy z=3+i
Ví d 2) Cho hai s phc 1 2
;
z z
tho mãn
1 2 1 2
; 3
z z z z= + = Tính
1 2
z z
−
Gii:
Đt
1 1 1 2 2 2
;
z a b i z a b i
= + = + . T gi thit ta có
( ) ( )
2 2 2 2
1 1 2 2
2 2
1 2 1 2
1
3
a b a b
a a b b
+ = + =
+ + + =
( ) ( ) ( )
2 2
1 1 2 2 1 2 1 2 1 2
2 1 1 1
a b a b a a b b z z
⇒+ = ⇒− + − = ⇒− =
Dng 2) Bài toán liên quan ñn nghim phc
Ví d 1) Gii phương trình sau:
2
8(1 ) 63 16 0
z i z i
− − + − =
Gii: Ta có
( )
2
2
' 16(1 ) (63 16 ) 63 16 1 8i i i i
∆ = − − − = − − = − T ñó tìm ra 2 nghim là
1 2
5 12 , 3 4
z i z i
= − = +
Ví d 2) Gii phương trình sau:
2
2(1 ) 4(2 ) 5 3 0i z i z i
+ − − − − =
Gii: Ta có
∆
’ = 4(2 – i)
2
+ 2(1 + i)(5 + 3i) = 16. Vy phương trình cho hai nghim là:
z
1
= i
ii
i
i
i
i
2
5
2
3
2
)1)(4(
1
4
)1(2
4)2(2 −=
−
−
=
+
−
=
+
+
−
z
2
= i
ii
i
i
i
i
2
1
2
1
2
)1)((
1)1(2
4)2(2 −−=
−
−
=
+
−
=
+
−
−
Ví d 3) Gii phương trình
3 2
9 14 5 0
z z z
− + − =
Gii:
Ta có ph
ươ
ng trình t
ươ
ng
ñươ
ng v
i
( )
( )
2
2 1 4 5 0
z z z
− − + = . T
ñ
ó ta suy ra
ph
ươ
ng trình có 3 nghi
m là
1 2 3
1; 2 ; 2
2
z z i z i
= = − = +
Ví d 4) Gii phương trình:
3 2
2 5 3 3 (2 1) 0
z z z z i
− + + + + =
bit phương trình có
nghim thc
Gii:
Vì ph
ươ
ng trình có nghi
m th
c nên
3 2
2 5 3 3 0
2 1 0
z z z
z
− + + =
+ =
1
2
z−
⇒= tho mãn c
hai phương trình ca h:Phương trình ñã cho tương ñương vi
( )
( )
2
2 1 3 3 0
z z z i
+ − + + = . Gii phương trình ta tìm ñưc
1; 2 ; 1
2
z z i z i
= − = − = +
www.laisac.page.tl
M
M
MỘ
Ộ
ỘT
T
TS
S
SỐ
Ố
ỐD
D
DẠ
Ạ
ẠN
N
NG
G
GB
B
BÀ
À
ÀI
I
IT
T
TẬ
Ậ
ẬP
P
P
V
V
VỀ
Ề
ỀS
S
SỐ
Ố
ỐP
P
PH
H
HỨ
Ứ
ỨC
C
C
NguyễnTrungKiên

2
Ví d 5) Gii phương trình: 3 2
(1 2 ) (1 ) 2 0
z i z i z i
+ − + − − = bit phương trình có
nghim thun o:
Gii: Gi s nghim thun o ca phương trình là z=bi thay vào phương trình ta có
( ) ( )
3 2 2 3 2
(1 2 ) (1 )( ) 2 0 ( ) ( 2 2) 0bi i bi i bi i b b b b b i+ − + − − = ⇔ − + − + + − =
2
3 2
01
2 2 0
b b b z i
b b b
− =
⇔⇒=⇒=
− + + − =
là nghi
m, t
ñ
ó ta có ph
ươ
ng trình t
ươ
ng
ñươ
ng v
i
( )
( )
2
(1 ) 2 0
z i z i z
− + − + = . Gii pt này ta s tìm ñưc các nghim
Ví d 6) Tìm nghim ca phương trình sau:
2
z z
=.
Gii: Gi s phương trình có nghim: z=a+bi thay vào ta có
( )
2
a bi a bi+ = +
2 2
2
a b a
ab b
− =
⇔= −
Gii h trên ta tìm ñưc 1 3
( , ) (0;0),(1;0),( ; )
2 2
a b = − ± . Vy phương
trình có 4 nghim là
1 3
0; 1; 2 2
z z z i
= = = − ±
Dng 3) Các bài toán liên quan ñn modun ca s phc:
Ví d 1) Tìm các s phc z tho mãn ñng thi các ñiu kin sau:
1 2 2
z i z i
+ − = − +
và
5z i− =
Gii:
Gi s z=x+yi (x,y là s thc) .T gi thit ta có
1 ( 2) 2 (1 )
( 1) | 5
x y i x y i
x y i
+ + − = − + −
+ − =
( )
( )
22 2 2
2
2
1 ( 2) ( 2) (1 )
1 5
x y x y
x y
+ + − = − + −
⇔+ − =
2
3
10 6 4 0
y x
x x
=
⇔− − =
1, 3
x y
⇔ = =
hoc
2 6
,
5 5
x y
= − = − . Vy có 2 s phc tho mãn ñiu kin.
Ví d 2) Xét s phc z tho mãn ;
1 ( 2 )
i m
z m R
m m i
−
= ∈
− −
a) Tìm m ñ 1
.2
z z =
b)Tìm m ñ 1
4
z i
− ≤
c) Tìm s phc z có modun ln nht.
Gii:
a) Ta có
( )
( )
( )( ) ( )
22 2 2
2
22 2 2 2
1 2 (1 ) 2 (1 2 )
1 2 1 2 1 2 1 4
i m m mi
i m m m m m m
zm mi m mi m mi m m
− − −
− − − + + − +
= = =
− + − + − − − +
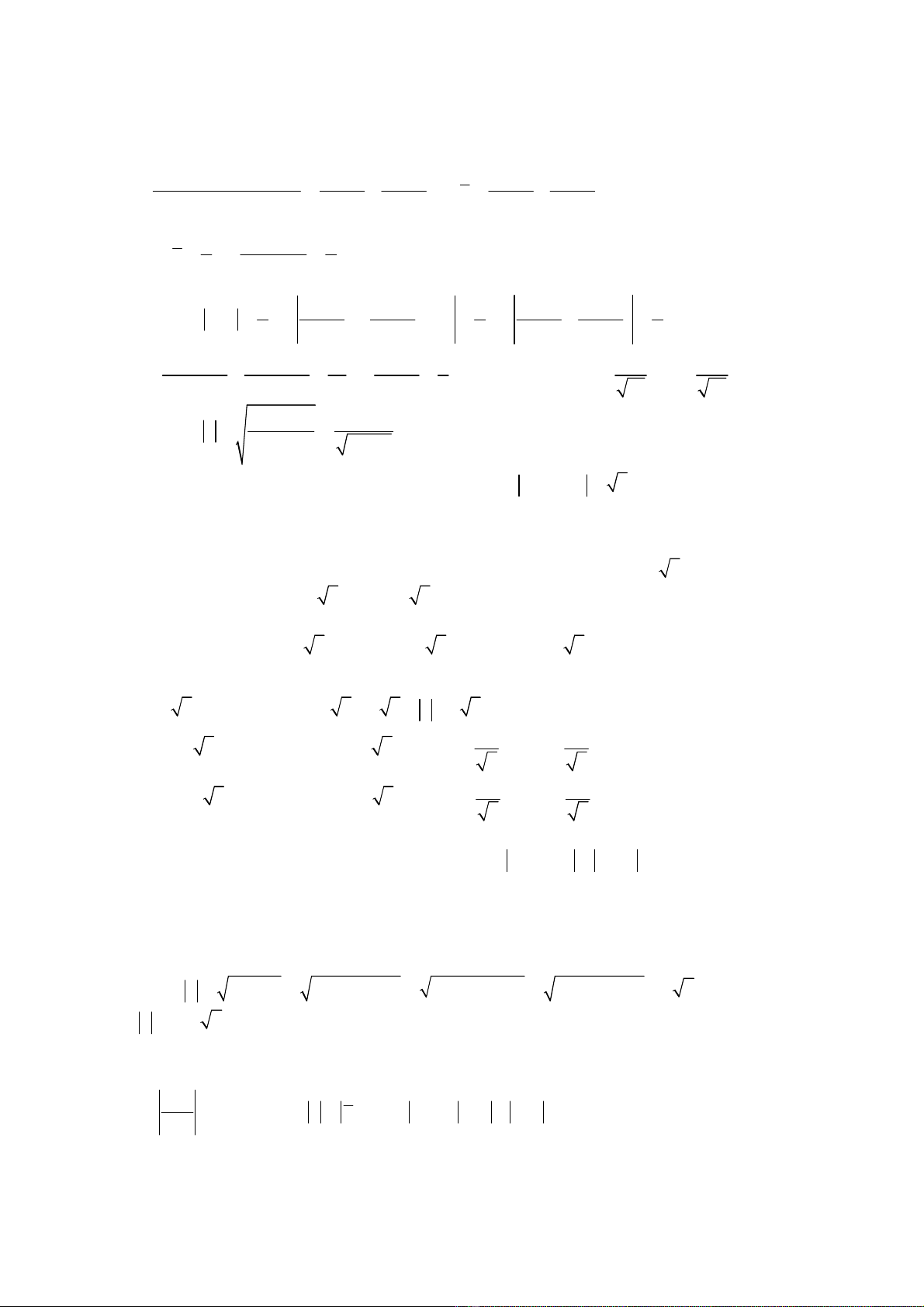
3
( )
2 2
22 2 2 2
2
(1 ) (1 ) 1 1
1 1 1 1
1
m m i m m m
i z i
m m m m
m
+ + +
= = + ⇒= −
+ + + +
+
( )
2
2
2
2
1 1 1
. 1 2 1
2 2
1
m
z z m m
m
+
⇒
= ⇔ = ⇔ + = ⇔ = ±
+
b) Ta có
2
2 2 2 2
1 1 1 1
1
4 1 1 4 1 1 4
m m m
z i i i
m m m m
− ≤ ⇔ + − ≤ ⇔ − ≤
+ + + +
⇔
2 4 2
2 2
2 2 2 2 2
1 1 1 1
16 1
(1 ) (1 ) 16 1 6 15 15
m m m m m m
m m m
⇔ + ≤ ⇔ ≤ ⇔ ≤ + ⇔ − ≤ ≤
+ + +
c) Ta có
( )
2
max
22
2
1 1 1 | | 1 0
1
1
m
z z m
m
m
+
= = ≤ ⇒= ⇔ =
+
+
Ví d 3) Trong các s phc z tho mãn ñiu kin 2 4 5z i− − = Tìm s phc z có
modun ln nht, nh nht.
Gii: Xét s phc z = x+yi . T gi thit suy ra
( ) ( )
2 2
2 4 5
x y
− + − = Suy ra tp hp
ñim M(x;y) biu din s phc z là ñưng tròn tâm I(2;4) bán kính 5R=
D dàng có ñưc (2 5 sin ;4 5 cos )M
α α
+ + . Modun s phc z chính là ñ dài véc tơ
OM.
Ta có |z|
2
=
2 2 2
(2 5 sin ) (4 5 cos ) 25 4 5(sin 2 cos )
OM
α α α α
= + + + = + +
Theo BDT Bunhiacopxki ta có
( )
2 2 2
(sin 2cos ) (1 4) sin cos 5
α α α α
+ ≤ + + =
5 sin 2cos 5
α α
⇒− ≤ + ≤ 5 3 5z⇒≤ ≤ . Vy
min
1 2
| | 5 sin 2cos 5 sin ;cos 1, 2 1 2
5 5
z
x y z i
α α α α
− −
=⇒+ = − ⇔ = = ⇔ = = ⇒= +
max
1 2
| | 3 5 sin 2 cos 5 sin ;cos 3, 6 3 6
5 5
z
x y z i
α α α α
= ⇔ + = ⇔ = = ⇔ = = ⇒= +
Ví d 4) Trong các s phc tho mãn ñiu kin
2 4 2
z i z i
− − = −
.Tìm s phc z có
moodun nh nht.
Gii: Xét s phc z = x+yi . T gi thit suy ra
( ) ( ) ( )
2 2 2
2
2 4 2 4 0
x y x y x y
− + − = + − ⇔ + − = Suy ra tp hp ñim M(x;y) biu din
s phc z là ñưng thng y=-x+4
Ta có
2 2 2 2 2 2
(4 ) 2 8 16 2( 2) 8 2 2
z x y x x x x x= + = + − = − + = − + ≥ . T ñó suy
min
2 2 2 2 2 2
z x y z i
= ⇔ = ⇒=⇒= +
Dng 4) Tìm tp hp ñim biu di n s phc
Ví d 1) Tìm tp hp các ñim M trong m!t ph"ng phc biu di n s phc z bit:
a)
3
z
z i =
−
b)
3 4
z z i
= − +
c)
4
z i z i
− + + =

4
Gii:
Gi z=x+yi
a) T gi thit ta có
2 2 2 2 2 2
9 9
3 9( ( 1) ) ( )
8 64
z z i x y x y x y= − ⇔ + = + − ⇔ + − =
Vy tp hp ñim M là ñưng tròn tâm 9 3
(0; ),
8 8
I R =
b) T gi thit ta có
( )
2
2 2 2
3 (4 ) 6 8 25
x y x y x y
+ = − + − ⇔ + = . Vy tp hp các ñim
M là ñưng thng 6x+8y-25=0
c) Gi s z =x+yi thì
4z i z i
− + + =
( ) ( )
2 2
2 2
1 1 4
x y x y
⇔ + − + + + = ⇔
( )
( ) ( ) ( )
( )
( )
2
22
2
2
2 2 2 2
2 2 2
1 16
1 4
2 1 4
1 16 8 1 1
x y
x y
x y y
x y x y x y
+ + ≤
+ + ≤
⇔ ⇔
+ − = +
+ − = − + + + + +
( ) ( )
2
2
2
2
2 2
2 2 2
1 16(1)
1 16
4 4 8 4 8 16 1(2)
3 4
44(3)
x y
x y x y
x y y y y
yy
+ + ≤
+ + ≤
⇔ + + + = + + ⇔ + =
≥ − ≥ −
Ta th
y các
ñ
i
m n
m trong hình tròn (1) và Elip (2) và tung
ñ
các
ñ
i
m n
m trên (Elip)
luôn tho
mãn
ñ
i
u ki
n y >-4. V
y t
p h
p
ñ
i
m M là Elip có pt
2 2
1
3 4
x y
+ = .
Ví d 2) Tìm tp hp các ñim biu di n trong m!t ph"ng phc s
phc
( )
1 3 2i z
ω
= + +
bit r#ng s phc z tho mãn:
1z
− ≤
2.
Gii:
Đ
t
( )
,
z a bi a b R
= + ∈
Ta có
1
z
− ≤
2
( )
22
1 4
a b
⇔ − + ≤ (1)
T
( ) ( )
( )
3 2 3 1 3
1 3 2 1 3 2 3 3 3( 1)
x a b x a b
i z x yi i a bi y a b y a b
ω
= − + − = − +
= + + ⇒+ = + + + ⇔ ⇔
= + − = − +
T ñó
( )
( )
( )
2
2 2 2
3 3 4 1 16
x y a b
− + − ≤ − + ≤
do (1)
Vy tp hp các ñim cn tìm là hình tròn
( )
( )
2
2
3 3 16
x y
− + − ≤ ; tâm
( )
3; 3I, bán
kính R=4.
Ví d 3) Xác ñ$nh tp hp các ñim M(z) trong m!t ph"ng phc biu di n các s
phc z sao cho s 2
2
z
z
−
+ có acgumen b#ng 3
π
.
Gii:

5
Gi s z=x+yi, thì
( )
( ) ( ) ( )
( )
22
2 2
2
2
2 2 2
x yi x yi
x yi
z
z x yi x y
− + + +
− +
−
= =
+ + + + +
( )
( )
( )
( )
2 2 2 2
2 2 2
2 2 2
4 2 2 4 4
2 2 2
x y yi x x x y y i
x y x y x y
− + + + − + + −
= = +
+ + − + − + (1)
Vì s
ph
c
2
2
z
z
−
+ có acgumen bng 3
π
, nên ta có:
( ) ( )
2 2
2 2
2 2
4 4 cos sin
3 3
2 2
x y y i i
x y x y
π π
τ
+ −
+ = +
− + − + v
i
0
τ
>
( )
( )
2 2
22
22
4
2
2
4 3
2
2
x y
x y
y
x y
τ
τ
+ − =
− +
⇒
=
− +
T ñó suy ra y>0 (1) và
2 2
2 2 2
2 2
4 4 2 4
3 4 (2)
43 3 3
y y
x y x y
x y
= ⇔ + − = ⇔ + − =
+ − .T (1) và (2) suy ra
tp hp các ñim M là ñưng tròn tâm nm phía trên trc thc(Trên trc Ox).
Dng 5) Chng minh bt ñ"ng thc:
Ví d 1) Chng minh r#ng nu
1
z≤ thì
2 1 1
2
z
iz
−≤
+
Gii:
Gi
s
z =a+bi (a, b
∈
R) thì
2 2 2 2
1 1
z a b a b
= + ≤ ⇔ + ≤ . Ta có
2 2
2 2
4 (2 1)
2 1 2 (2 1)
2 (2 ) (2 )
a b
z a b i
iz b ai b a
+ −
− + −
= =
+ − + − + .Bt ñng thc cn chng minh tương ñương
vi
2 2
2 2 2 2 2 2
2 2
4 (2 1) 1 4 (2 1) (2 ) 1
(2 )
a b a b b a a b dpcm
b a
+ − ≤ ⇔ + − ≤ − + ⇔ + ≤ ⇒
− +
Ví d 2) Cho s phc z khác không tho mãn ñiu kin 3
3
12
zz
+ ≤ . Chng minh
r#ng: 12
zz
+ ≤
Gii: D dàng chng minh ñưc vi 2 s phc 1 2
,
z z
bt kỳ ta có
1 2 1 2
z z z z
+ ≤ +
Ta có
3 3
3 3
3 3
1 1 1 1 1 1 1
3 3 2 3z z z z z z z
z z z z z z z
+ = + + + ⇒+ ≤ + + + ≤ + +
Đt 1
z
z
+=a ta có
( )( )
2
3
3 2 0 2 1 0
a a a a dpcm
− − ≤ ⇔ − + ≤ ⇒


























