Tìm giao tuyến của hai mặt phẳng

Tài liệu ôn thi THPT Quốc gia năm 2024 môn Toán - Chuyên đề 30: Phương trình mặt phẳng (Tài liệu dành cho đối tượng học sinh giỏi mức 9-10 điểm) tập trung vào các bài toán phương trình mặt phẳng mức độ nâng cao, bao gồm xác định giao tuyến của hai mặt phẳng, tìm phương trình mặt phẳng tiếp xúc với mặt cầu, và ứng dụng trong bài toán cực trị hình học. Học sinh sẽ được tiếp cận hệ thống bài tập trắc nghiệm khó và các chiến lược giải bài nhanh. Mời các bạn cùng tham khảo tài liệu "Tài liệu ôn thi THPT Quốc gia năm 2024 môn Toán - Chuyên đề 30" để học tập và đạt kết quả cao.

181p tinhtamdacy555 29-03-2025 4 1   Download

Giáo án điện tử Hình học 11 - Chương 2, Tiết 13: Luyện tập Đại cương về đường thẳng và mặt phẳng giúp học sinh củng cố kiến thức và làm quen với các dạng bài tập nhận biết, tìm giao tuyến của hai mặt phẳng, tìm giao điểm của đường thẳng và mặt phẳng, tìm thiết diện của hình chóp và mặt phẳng. Thông qua luyện tập, học sinh rèn luyện kỹ năng vẽ hình, tư duy logic và phương pháp giải bài toán hình học không gian một cách hiệu quả.

15p tuongtieume 28-03-2025 8 1   Download

Mục đích của đề tài nghiên cứu nhằm phát triển tư duy và rèn luyện kỹ năng giải các bài tập liên quan đến góc giữa hai mặt phẳng cho học sinh khá, giỏi. Nâng cao hiệu quả trong việc ôn thi THPT Quốc gia. Đề tài áp dụng hiệu quả cho đối tượng học sinh khá, giỏi lớp 11, 12.

24p ganuongmuoiot 02-08-2021 54 5   Download

BÀI 1: ĐẠI CƯƠNG VỀ ĐƯỜNG THẲNG VÀ MẶT PHẲNG Vấn đề 1 : TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG α VÀ β : Muốn tìm giao tuyến của hai mặt phẳng α và β ta đi tìm hai điểm chung I ; J của α và β α

23p huyenchauthuc 30-05-2013 112 7   Download

Bài giảng "Hình học lớp 11: Hai đường thẳng chéo nhau và hai đường thẳng song song" được biên soạn nhằm giúp các em học sinh nắm được vị trí tương đối của hai đường thẳng, khái niệm hai đường thẳng chéo nhau; Tìm giao tuyến của hai mặt phẳng cách thứ 2; Nắm và áp dụng được định lý về ba mặt phẳng cắt nhau theo 3 giao tuyến. Mời quý thầy cô và các em cùng tham khảo bài giảng.

25p chieuchieu01 15-04-2023 20 4   Download

Mời quý thầy cô và các em học sinh tham khảo “Đề cương ôn tập học kì 1 môn Toán lớp 11 năm 2024-2025 - Trường THPT Yên Hòa, Hà Nội”. Hi vọng tài liệu sẽ là nguồn kiến thức bổ ích giúp các em củng cố lại kiến thức trước khi bước vào kì thi sắp tới. Chúc các em ôn tập kiểm tra đạt kết quả cao!

40p gaupanda055 14-10-2024 15 1   Download

Giáo án Toán lớp 11 - Chương IV, Bài 3: Đường thẳng và mặt phẳng song song (Sách Chân trời sáng tạo) được biên soạn với mục tiêu nhằm giúp học sinh nêu được các định nghĩa và các dấu hiệu nhận biết vị trí tương đối của đường thẳng và mặt phẳng bao gồm: đường thẳng song song với mặt phẳng, đường thẳng cắt mặt phẳng. Biết sử dụng các định lý về quan hệ song song để chứng minh đường thẳng song song với mặt phẳng, tìm giao tuyến của hai mặt phẳng.

12p trieungocchan 07-09-2023 12 2   Download

Đề cương ôn tập Học kì 1 môn Toán của trường THPT Ngô Tất Tố giúp các bạn củng cố được kiến thức về phương pháp giải lượng giác, tổ hợp - xác suất, cấp số cộng; cách tìm giao điểm của một đường thăng và mặt phẳng, giao tuyến của hai mặt phẳng, dựng thiết diện song song với mặt phẳng.

3p manhhungda1 13-03-2015 139 11   Download

Nắm được kiến thức cơ bản của hai mặt phẳng song song: về định nghĩa và các định.lý..Về kỹ năng: -Biết cách vận dụng các định lí vào việc chứng minh hai đường thẳng song song.. - Tìm giao tuyến, giao điểm.B. Chuẩn bị: Giáo viên: Giáo án, dụng cụ dạy học..

20p suutoan 04-09-2013 80 17   Download

Trên mặt phảng tọa độ, gọi (P) là đồ thị hàm số y  x 2 a, Vẽ (P) b, Tìm tọa độ giao điểm của (P) và đường thẳng d: y = -2x+3 Câu 4:(1,5 điểm) Hai xe khởi hành cùng một lúc đi từ địa điểm A đến địa điểm B cách nhau 100km. Xe thứ nhất chạy nhanh hơn xe thứ hai 10km/h nên đã đến B sớm hơm 30 phút

3p nhungmuadauyeu123 19-06-2013 85 5   Download

Phương pháp 1: Tìm hai điểm chung phân biệt của hai mặt phẳng. Ví dụ: Cho hình chóp SABCD.Tìm giao tuyến của hai mặt phẳng (SAC) và (SBD). Giải: Trong mặt phẳng (ABCD): AC cắt BD tại O. Ta có O  AC, AC  (SAC) O  BD, BD  (SBD) Nên O là điểm chung của hai mặt phẳng (SAC) và (SBD) Mà S là điểm chung của hai mặt phẳng (SAC) và (SBD) Vậy SO là giao tuyến của (SAC) và (SBD). ♦Phương pháp 2: Sử dụng định lý: Nếu hai mặt phẳng cắt nhau lần lượt...

5p paradise10 29-12-2011 1551 120   Download

Nắm được các khái niệm điểm đường thẳng & mặt phẳng trong không gian. Các tính chất thừa nhận. Các cách xác định mặt phẳng để vận dụng vào bài tập  Về kĩ năng : Biết cách tìm giao điểm của đường thẳng với mặt phẳng. Tìm giao tuyến của hai mặt phẳng .Chứng minh 3 điểm thẳng hàng. Tìm thiết diện của hình chóp khi cắt bởi một mặt phẳng.  Về tư duy & thái độ : Tích cực hoạt động , quan sát & phán đoán chính xác...

7p abcdef_47 10-11-2011 409 25   Download

Cho bôń điêm̉ A,B,C va ̀ D không đôǹ g phăn̉ g. Goị I, K lâǹ lươṭ la ̀ trung điêm̉ cuả AD va ̀ BC. Tim̀ giao tuyêń cuả hai mp(IBC) va ̀ mp(KAD)...

11p lminhv 19-08-2011 186 34   Download

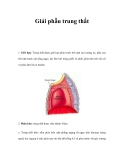
Trung thất được giới hạn phía trước bởi mặt sau xương ức, phía sau bởi mặt trước cột sống ngực, hai bên bởi màng phổi và phổi, phía trên bởi nền cổ và phía dưới là cơ hoành. 2. Phân khu: trung thất được chia thành 4 khu: a. Trung thất trên: nằm phía trên mặt phẳng ngang đi ngay trên khoang màng ngoài tim (ngang ở mức phía sau với khe đốt sống 4,5 và phía trước với góc xương ức): chứa tuyến ức, khí quản, các mạch máu lớn của tim, các nhánh của nó và các dây thần...

4p truongthiuyen2 10-06-2011 274 22   Download

1. Tìm giao tuyến của hai mặt phẳng (cách 1) Phương pháp : - Tìm điểm chung của 2 mặt phẳng - Đường thẳng qua hai điểm chung đó là giao tuyến của hai mặt phẳng

9p quang9kd 05-04-2011 1788 475   Download

Tìm giao tuyến của hai mặt phẳng (cách 1) Phương pháp: Tìm điểm chung của 2 mặt phẳng Đường thẳng qua hai điểm chung đó là giao tuyến của hai mặt phẳng Chú ý : Để tìm điểm chung của hai mặt phẳng ta thường tìm hai đường thẳng đòng phẳng lần lượt nằm trong hai mặt phẳng đó . Giao điểm , nếu có của hai đường thẳng này chính là điểm chung của hai mặt phẳng .

7p nyegun 19-09-2010 1507 557   Download

A.PHƯƠNG PHÁP: Cách thường dùng để xác định góc giữa hai mp (P) và (Q) là: *xác định giao tuyến ∆ của (P) và (Q). *Trên (P) tìm AI ⊥ ∆ ,trên (Q) tìm BI.⊥ ∆ *AIB là góc cần tìm (còn gọi là góc phẳng của nhị diện ((P),(Q)). Cách chứng minh hai mặt phẳng (P),(Q) vuông góc với nhau: *Chứng minh góc giữa chúng bằng 90 *Chứng minh (P) chứa một đường thẳng vuông góc với (Q).

9p huynhphuoc 06-03-2010 3176 217   Download

CHƯƠNG II:QUAN HỆ SONG SONG CHỦ ĐỀ 1: TÌM GIAO TUYẾN CỦA HAI MẶT PHẲNG. A.PHƯƠNG PHÁP: Để tìm giao tuyến của hai mặt phẳng ta tìm hai điểm chung phân biệt của hai mặt phẳng đó. B.VÍ DỤ: Ví dụ 1:

11p huynhphuoc 21-12-2009 691 200   Download

Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn .Gọi M,N theo thứ tự là trung điểm của các cạnh SB,SC. a) Tìm giao tuyến hai mặt phẳng (SAD) và (SBC). b)Tìm giao điểm của đường thẳng SD với mặt phẳng(AMN).

3p phuong20078 06-12-2009 2364 157   Download

Cho 4 điểm A,B,C,D không cùng nằm trong một mặt phẳng a)Chứng minh rằng hai đường thẳng AB và CD chéo nhau b)Trên các đoạn AB và AD lần lượt lấy các điểm M và N sao cho đường thẳng MN cắt đường thẳng BD tại I.Hãy xét xem điểm I thuộc những mặt phẳng nào ?Tìm giao tuyến của hai mặt phẳng (CMN) và (BCD)

10p theanh1992 12-11-2009 1890 352   Download