ĐỊNH THỨC
Ts. Lê Xuân Trường
Khoa Toán Thống Kê
Ts. Lê Xuân Trường (Khoa Toán Thống Kê) ĐỊNH THỨC 1 / 8
Ma trận con bù
Cho A=(aij )là ma trận vuông cấp n.
Abỏ dòng i
−−−−−→
bỏ cột j
Mij
↓
ma trận con bù của aij
Ví dụ: Xét ma trận
A=
2−1 3
1 4 −5
−3 2 −2
ma trận con bù của a12:M12 =1−5
−3−2
ma trận con bù của a31:M31 =−1 3
4−5
Ts. Lê Xuân Trường (Khoa Toán Thống Kê) ĐỊNH THỨC 2 / 8
Khái niệm định thức
Cho A=(aij )là ma trận vuông cấp n. Định thức của Alà một số thực,
ký hiệu bởi det(A), và được xác định bởi qui nạp theo nnhư sau
n=2:
A=a11 a12
a21 a22⇒det(A) = a11a22 −a12a21
Ví dụ:A=1 2
3 4⇒det(A) = −2
n≥3:
det(A) = (−1)k+1ak1det(Mk1) + ···+ (−1)k+nakndet(Mkn)
(với kbất kỳ trong tập {1,2, ..., n})
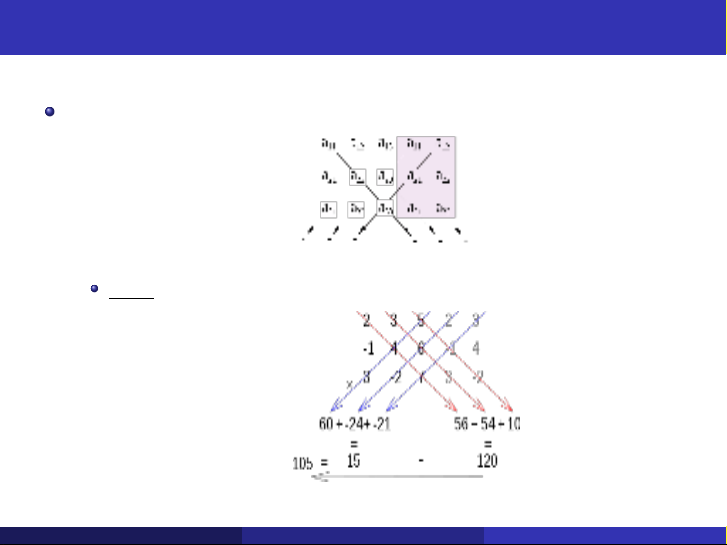
Ví dụ: Tính định thức của ma trận A=
−122
3 1 4
−231
Ts. Lê Xuân Trường (Khoa Toán Thống Kê) ĐỊNH THỨC 3 / 8
Qui tắc Sarrus (tính định thức cấp 3)
Qui tắc Sarrus
Ví dụ:
Ts. Lê Xuân Trường (Khoa Toán Thống Kê) ĐỊNH THỨC 4 / 8
Lưu ý
Ta có thể tính định thức bằng cách khai triển theo một cột bất kỳ
Ví dụ: Tính định thức của ma trận sau
A=
3 1 0 2
−1 2 0 3
1−2 0 1
2−1−2 0
Khai triển theo cột thứ 3
det(A) = (−1)4+3(−2)
3 1 2
−1 2 3
1−2 1
=28
Ts. Lê Xuân Trường (Khoa Toán Thống Kê) ĐỊNH THỨC 5 / 8