BÀI GIẢNG
KINH TẾ LƯỢNG
ECONOMETRICS
Lê Anh Đức
Khoa Toán kinh tế
ĐH Kinh tế Quốc dân
1
CHƯƠNG II: MÔ HÌNH HỒI QUY HAI BIẾN,
ƯỚC LƯỢNG VÀ KIỂM ĐỊNH GIẢ THIẾT
2.1. Phương pháp bình phương nhỏ nhất (OLS)
2.2. Các giả thiết cơ bản của phương pháp OLS
2.3. Độ chính xác của các ước lượng OLS
2.4. Hệ số r2đo độ phù hợp của hàm hồi quy mẫu
2.5. Phân bố xác suất của Ui
2.6. Khoảng tin cậy và kiểm định giả thiết về các hệ số hồi quy
2.7. Kiểm định sự phù hợp của hàm hồi quy, phân tích hồi quy và
phân tích phương sai
2.8. Phân tích hồi quy và dự báo
2.9. Trình bày kết quả phân tích hồi quy
2.10. Thí dụ
2
2.1. Phương pháp bình phương nhỏ nhất - OLS
1. Nội dung của phương pháp OLS
• Xét mô hình hồi quy đơn dạng tuyến tính
PRF: E(Y/Xi)=
1+
2Xi
PRM: Yi=
1+
2Xi+ Ui
• Với mẫu W = {(Xi, Yi), i = 1÷ n} tìm được một ước lượng
điểm của PRF
SRF:
SRM:
1 2
ˆ ˆ
ˆ
i i
Y
β β X
1 2
ˆ ˆ
i i i
Y
β β X e
3
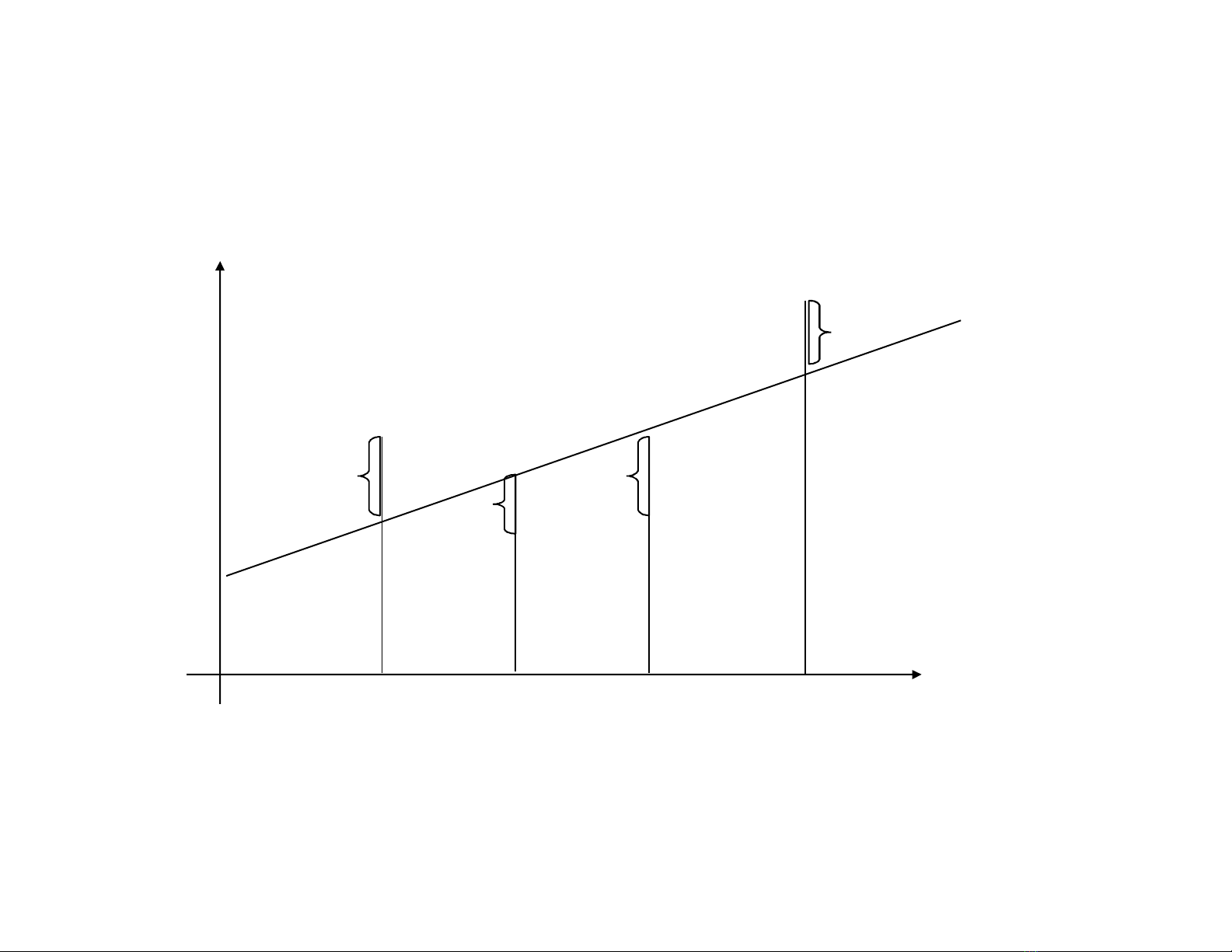
• Đồ thị
X1X2X3X4
e4
e3
e2
e1
SRF
Y
X
4
• Nội dung của phương pháp OLS là tìm các
ước lượng điểm sao cho tổng bình
phương các phần dư là nhỏ nhất. Tức là sao
cho càng gần với giá trị thực của Yicó
thể được.
• Tìm sao cho:
1 2
,
β β
ˆ
i
Y
2
2
1 1
ˆ
min
n n
i i i
i i
e Y Y
1 2
ˆ ˆ
,
β β
5