intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Bài giảng Quản lý danh mục đầu tư: Chương 2 - ThS. Nguyễn Phạm Thi Nhân

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:123

Thêm vào BST
Báo xấu
2
lượt xem 0
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Bài giảng "Quản lý danh mục đầu tư" Chương 2 - Lý thuyết markowitz, được biên soạn gồm các nội dung chính sau: Lợi suất và rủi ro của danh mục đầu tư; đa dạng hóa danh mục đầu tư; mô hình markowitz;...Mời các bạn cùng tham khảo!

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Bài giảng Quản lý danh mục đầu tư: Chương 2 - ThS. Nguyễn Phạm Thi Nhân

  1. TRƯỜNG ĐẠI HỌC NGÂN HÀNG TP.HCM QUẢN LÝ DANH MỤC ĐẦU TƯ CHƯƠNG 2: LÝ THUYẾT MARKOWITZ ThS. Nguyễn Phạm Thi Nhân 1
  2. CHƯƠNG 2: LÝ THUYẾT MARKOWITZ 2.1. LỢI SUẤT & RỦI RO CỦA DMĐT ⚫ 2.1.1. Lợi suất kỳ vọng và rủi ro của chứng khoán riêng lẻ ⚫ 2.1.2. Lợi suất kỳ vọng của danh mục đầu tư. ⚫ 2.1.3. Đo lường sự tương quan giữa các tài sản đầu tư. ⚫ 2.1.4. Rủi ro của danh mục đầu tư ⚫ 2.1.5. Ứng dụng tin học tính toán lợi nhuận, rủi ro DMĐT 2.2. ĐA DẠNG HÓA DANH MỤC ĐẦU TƯ ⚫ 2.2.1. Vai trò của đa dạng hóa ⚫ 2.2.2. Ảnh hưởng của mối tương quan giữa các CK lên quá trình đa dạng hóa DMĐT ⚫ 2.2.3.Phân tích rủi ro tổng thể, hiệu quả của việc đa dạng hóa. ThS. Nguyễn Phạm Thi Nhân 2
  3. CHƯƠNG 2: LÝ THUYẾT MARKOWITZ (tt) 2.3. MÔ HÌNH MARKOWITZ ⚫ 2.3.1. Các giả thiết của mô hình ⚫ 2.3.2. Mức ngại rủi ro và hàm hiệu dụng ⚫ 2.3.3. Danh mục đầu tư hiệu quả ⚫ 2.3.4. Lựa chọn danh mục đầu tư tối ưu ⚫ 2.3.5. Ứng dụng tin học trong việc tìm danh mục đầu tư hiệu quả và DMĐT tối ưu ThS. Nguyễn Phạm Thi Nhân 3
  4. 2.1. LỢI SUẤT & RỦI RO CỦA DMĐT MỨC SINH LỜI MỨC SINH LỜI TÍNH BẰNG GIÁ TRỊ TUYỆT ĐỐI  Mức sinh lời của một khoản đầu tư là phần chênh lệch giữa kết quả thu được sau một khoảng thời gian đầu tư và vốn gốc mà nhà đầu tư đã bỏ ra ban đầu. ThS. Nguyễn Phạm Thi Nhân  Mức sinh lời xuất phát từ 2 nguồn :  Cổ tức / Trái tức  Chênh lệch giữa giá bán và giá mua ( Lợi vốn / Lỗ vốn ) Mức sinh Cổ tức Lợi vốn lời tuyệt = + (Trái tức) (Lỗ vốn) đối 4
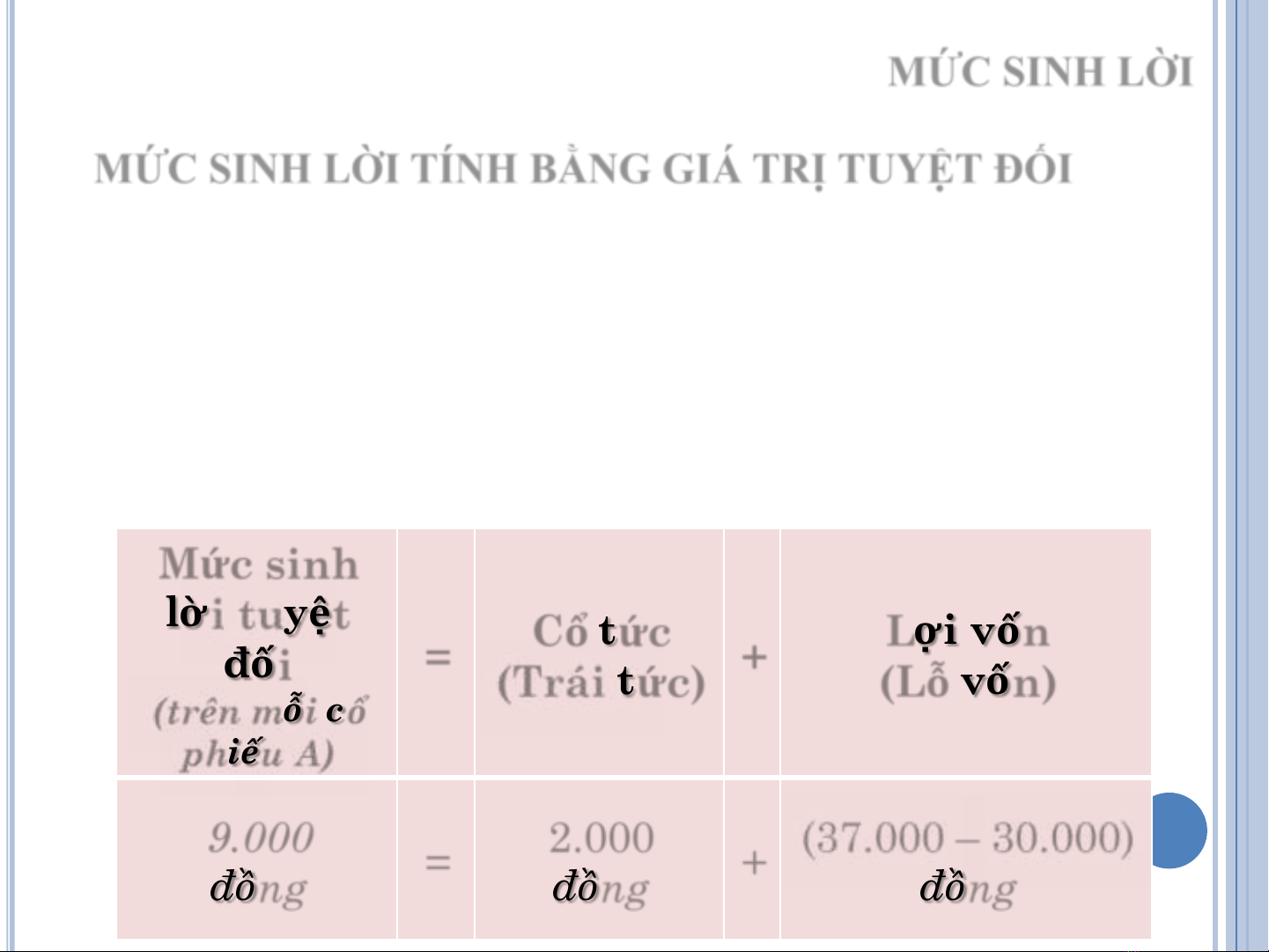
  5. MỨC SINH LỜI MỨC SINH LỜI TÍNH BẰNG GIÁ TRỊ TUYỆT ĐỐI  Ví dụ: Nếu nhà đầu tư mua cổ phiếu A vào đầu năm với giá 30.000 đồng, trong năm nhà đầu tư nhận được cổ tức ThS. Nguyễn Phạm Thi Nhân 2.000 đồng/CP và giá cổ phiếu A cuối năm là 37.000 đồng.  Như vậy : Mức sinh lời tuyệt Cổ tức Lợi vốn đối = + (Trái tức) (Lỗ vốn) (trên mỗi cổ phiếu A) 9.000 2.000 (37.000 – 30.000) 5 = + đồng đồng đồng
  6. MỨC SINH LỜI MỨC SINH LỜI TÍNH THEO PHẦN TRĂM  Mức sinh lời tính theo phần trăm sẽ cho biết nếu bỏ ra một đồng đầu tư thì ta sẽ thu về được bao nhiêu đồng. ThS. Nguyễn Phạm Thi Nhân  Đây là cơ sở để so sánh các khoản đầu tư với nhau  Tính mức sinh lời theo phần trăm: Mức Mức sinh lời theo giá trị tuyệt đối sinh = lời Tổng vốn đầu tư ban đầu tính theo DiV1 + ( P1 – P0) phần trăm = (R1) P0 6
  7. MỨC SINH LỜI MỨC SINH LỜI TÍNH THEO PHẦN TRĂM  Ví dụ: Nếu nhà đầu tư mua cổ phiếu A vào đầu năm với giá 30.000 đồng, trong năm nhà đầu tư nhận được cổ tức 2.000 ThS. Nguyễn Phạm Thi Nhân đồng/CP và giá cổ phiếu A cuối năm là 37.000 đồng.  Tính mức sinh lời theo phần trăm: DiV1 + ( P1 – P0) Mức sinh = lời P0 tính theo 2.000 + ( 37.000 – 30.000) phần trăm = = 30% (R1) 30.000  DiV1 / P0 : Tỉ lệ cổ tức = 6,67% 7  (P1-P0)/P0 : Tỉ lệ lãi vốn = 23,33%
  8. MỨC SINH LỜI MỨC SINH LỜI TÍNH THEO PHẦN TRĂM DiV1 + ( P1 – P0) Mức sinh = P0 ThS. Nguyễn Phạm Thi Nhân lời tính theo 2.000 + ( 37.000 – 30.000) phần trăm = = 30% (R1) 30.000 Với:  R1 : Mức sinh lời trong giai đoạn từ khi mua ( thời điểm 0) tới thời điểm 1 năm sau.  DiV1: Cổ tức thu được trong giai đoạn này  P0 : Giá mua 8  P1 : Giá tại thời điểm 1 năm sau
  9. MỨC SINH LỜI MỨC SINH LỜI TÍNH THEO PHẦN TRĂM  Tỷsuất lợi nhuận của chứng khoán còn được tính dựa trên công thức lợi nhuận tích gộp liên tục. ThS. Nguyễn Phạm Thi Nhân r = Ln[(D1+P1)/P0] Ví dụ trên : Nếu nhà đầu tư mua cổ phiếu A vào đầu năm với giá 30.000 đồng, trong năm nhà đầu tư nhận được cổ tức 2.000 đồng/CP và giá cổ phiếu A cuối năm là 37.000 đồng. r = Ln[2000+37000)/30000] = 26,24% 9
  10. MỨC SINH LỜI MỨC SINH LỜI BÌNH QUÂN SỐ HỌC  Xét một cách giản đơn nhất: R1 + R 2 + ... + R n ThS. Nguyễn Phạm Thi Nhân R= n  Trong đó:  R : mức sinh lời bình quân năm  R1, R2, Rn : mức sinh lời từng năm trong khoảng đầu tư t năm  Ta cũng có thể dùng công thức này để xác định lợi nhuận kỳ vọng cho tương lai ( phương pháp dựa vào dữ liệu quá khứ) – hoặc có thể dực vào phương pháp dự báo tình huống để ước tính lợi nhuận kỳ vọng của một khoản đầu tư. 10
  11. MỨC SINH LỜI MỨC SINH LỜI BÌNH QUÂN SỐ HỌC  Phương pháp này chưa hẳn là hợp lý ??? Giai đoạn 1 Giai đoạn 2 ThS. Nguyễn Phạm Thi Nhân TB 2 giai t= 0 (t=1) (t=2) đoạn Giá Giá TSLN Giá TSLN R A 100 đ 110 đ 10% 121 10,0% 10,00% B 100 đ 150 đ 50% 121 -19,3% 15,33% C 100 đ 200 đ 100% 121 -39,5% 30,25%  Dường như cổ phiếu C cho kết quả tốt hơn , nhưng rõ ràng là sai 11
  12. MỨC SINH LỜI MỨC SINH LỜI TRONG MỘT KHOẢNG THỜI GIAN  Tổng mức sinh lời trong nhiều năm: Rt năm = (1+R1)(1+R2)....(1+Rt) - 1 ThS. Nguyễn Phạm Thi Nhân  Mức sinh lời bình quân hàng năm: R = t (1 + R1 )(1 + R 2 )....(1 + R t ) − 1  Lưu ý: công thức được xây dựng trên giả định cổ tức được tái đầu tư với mức sinh lời tương tự khoản vốn gốc.  Mức sinh lời tháng quy đổi thành mức sinh lời năm: R năm = (1+ R m tháng) 12/m - 1 12  Nếu có thuế thì phải tính mức sinh lời thực thu sau khi loại thuế
  13. MỨC SINH LỜI MỨC SINH LỜI TRONG MỘT KHOẢNG THỜI GIAN  Ví dụ: Nếu mức sinh lời qua là 11%, -5%, 9% trong khoảng thời gian 3 năm thì tổng mức sinh lời của 3 năm ThS. Nguyễn Phạm Thi Nhân sẽ bằng bao nhiêu? Và mức sinh lời trung bình lũy kế hàng năm sẽ là bao nhiêu? Rt năm = (1+11%)(1-5%)(1+9%) – 1 = 14,94% R = 3 (1 + 11%)(1 − 5%)(1 + 9%) − 1 = 4,75% 13
  14. MỨC SINH LỜI MỨC SINH LỜI TRONG MỘT KHOẢNG THỜI GIAN  Vídụ: Chỉ số VN-index tháng 7/2000 là 100 điểm, tháng 7/2014 là 400 điểm, hãy tính tỉ ThS. Nguyễn Phạm Thi Nhân suất sinh lời bình quân của thị trường này? R= 14 400 / 100 − 1 = 10,409% 14
  15. MỨC SINH LỜI MỨC SINH LỜI BÌNH NHÂN  Phương pháp cho kết quả chuẩn xác hơn: Giai đoạn 1 Giai đoạn 2 ThS. Nguyễn Phạm Thi Nhân TB 2 giai t= 0 (t=1) (t=2) đoạn R bình quân Giá Giá TSLN Giá TSLN nhân A 100 đ 110 đ 10% 121 đ 10,0% 10,00% B 100 đ 150 đ 50% 121 đ -19,3% 10,00% C 100 đ 200 đ 100% 121 đ -39,5% 10,00%  Tỷ suất sinh lời cho kỳ đầu tư 2 năm của ba cổ phiếu trung bình đạt 10,00%/năm 15
  16. MỨC SINH LỜI MỨC SINH LỜI BÌNH QUÂN TRỌNG SỐ (TỶ LỆ NỘI HOÀN IRR)  Mức sinh lời này được tính khi nhà đầu tư muốn đánh giá kết quả sinh lời bình quân mỗi năm trong cả một giai đoạn đầu tư dài hạn với các dòng tiền thu hồi về tại các thời điểm khác ThS. Nguyễn Phạm Thi Nhân nhau.  Hay nói cách khác IRR chính là tỷ suất hoàn vốn.  Ví dụ: Vốn đầu tư ban đầu 1 tỉ đồng, dòng tiền thu hồi 4 năm như sau: Năm 1 2 3 4 Dòng tiền thu được -0.1 -0.5 0.8 1 ( tỉ đồng) -0.1 -0.5 0.8 1 1 = + + + (1+IRR) (1+IRR) (1+IRR) (1+IRR) 16 Vậy IRR = 4.17%
  17. MỨC SINH LỜI MỨC SINH LỜI BÌNH QUÂN TRỌNG SỐ (TỶ LỆ NỘI HOÀN IRR)  Cách nội suy xác định IRR:  Chọn i1 sao cho NPV1 > 0 ThS. Nguyễn Phạm Thi Nhân  Chọn i2 sao cho NPV2
  18. 2.1.1. LỢI NHUẬN KỲ VỌNG & RỦI RO CỦA CHỨNG KHOÁN RIÊNG LẺ: ⚫ Xác định lợi nhuận sau khi kết thúc một phi vụ làm ăn? → Rất đơn giản!!! = Doanh thu – Chi phí ⚫ Làm thế nào để ước tính lợi nhuận có thể thu được để quyết định có nên đầu tư hay không? → Khó khăn và phức tạp! Chẳng thể nào biết chính xác những gì chưa xảy ra! Lợi nhuận kỳ vọng HAY Lợi nhuận mong đợi Expected return (Er) ThS. Nguyễn Phạm Thi Nhân 18
  19. LỢI NHUẬN KỲ VỌNG CK RIÊNG LẺ (Expected Return) Ví dụ 2: Bạn định đầu tư vào CP Sacom. Theo phân tích thì thu nhập của CP Sacom có thể có những khả năng sau: Khả năng Xấu Trung bình Tốt Xác suất 0,2 0,5 0,3 Thu nhập (R) 5% 15 % 25 % Như vậy, lợi nhuận kỳ vọng (Er) chính là kỳ vọng của đại lượng ngẫu nhiên R với luật phân phối: Ri 5% 15 % 25 % Pi 0,2 0,5 0,3 ThS. Nguyễn Phạm Thi Nhân 19
  20. Ví dụ 2: Bạn định đầu tư vào cổ phiếu Sacom. Theo phân tích thì thu nhập của cổ phiếu Sacom có thể có những khả năng sau: Khả năng Xấu Trung bình Tốt Xác suất 0,2 0,5 0,3 Thu nhập (R) 5% 15 % 25 % Như vậy, lợi nhuận kỳ vọng (Er) chính là kỳ vọng của đại lượng ngẫu nhiên R với luật phân phối: Ri 5% 15 % 25 % Pi 0,2 0,5 0,3 E(r) = 5%*0,2+15%*0,5+25%*0,3 = 16% ThS. Nguyễn Phạm Thi Nhân 20
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright ©2025 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
11=>2