
Bai tâp môt số phương trinh lượng giac thường găp
lượt xem 166
download
 Download
Vui lòng tải xuống để xem tài liệu đầy đủ
Download
Vui lòng tải xuống để xem tài liệu đầy đủ
Giúp HS nắm vững cách giải một số PTLG mà sau một vài phép biến đổi đơn giản có thể đưa về PTLGCB. Đó là PT bậc nhất và bậc hai đối với một HSLG...
Bình luận(0) Đăng nhập để gửi bình luận!
Nội dung Text: Bai tâp môt số phương trinh lượng giac thường găp
- Bai tâp môt số phương trinh lượng giac thường găp ̣̀ ̣ ̀ ́ ̣ MỘT SỐ PHƯƠNG TRÌNH LƯỢNG GIÁC THƯỜNG GẶP A. MỤC TIÊU. 1. Về kiến thức : Giúp HS nắm vững cách giải một số PTLG mà sau một vài phép biến đổi đơn giản có thể đưa về PTLGCB. Đó là PT bậc nhất và bậc hai đối với một HSLG 2. Về kỹ năng : Giúp HS nhận biết và giải thành thạo các dạng PT trong bài 3. Về tư duy thái độ : Có tinh thần hợp tác, tích cực tham gia bài học, rèn luyện tư duy logic. B. TOM TĂT KIÊN THỨC ́ ́ ́ Bài toán 1: Phương trình bậc nhất đối với một hàm số lượng giác Phương pháp chung: - Chuyển về PT lượng giác cơ bản Bài toán 2: Phương trình bậc hai đối với một hàm số lượng giác Phương pháp chung: - Có dạng: a [ f ( x )] + bf ( x) + c = 0 (a ≠ 0) 2 Bài toán 3: Phương trình bậc nhất đối với sinx và cosx Phương pháp chung: - Có dạng: a sin x + b cos x = c - Đ/k có nghiệm: a2 + b2 ≥ c2 - P2 giải: Chia cả hai vế PT cho a 2 + b 2 , sau đó đưa về PT lượng giác cơ bản. Bài toán 4: Phương trình bậc hai thuần nhất đối với sinx và cosx Phương pháp chung: - Có dạng: a sin 2 x + b.sin x.cos x + c cos 2 x = d - P2 giải: + Nhận xét cosx = 0 không thỏa mãn PT + Vậy cosx ≠ 0. Chia cả hai vế PT cho cos2x ta được PT: a tan 2 x + btanx + c = 0 là phương trình bậc hai đối với tanx Bài toán 5: Một số phưong trình lượng giác khác Phương pháp chung: - Dùng công thức lượng giác đưa PT về dạng tích ̣ ̀ ̣ C. NÔI DUNG BAI DAY II. PHƯƠNG TRÌNH BẬC HAI ĐỐI VỚI MỘT HÀM SỐ LƯỢNG GIÁC Dạng Đặ t Điều kiện −1 ≤ t ≤ 1 t = sinx 2 asin x + b sin x + c = 0 −1 ≤ t ≤ 1 t = cosx a cos2 x + b cos x + c = 0 π a tan2 x + b tan x + c = 0 + kπ (k ∈ Z ) x≠ t = tanx 2 x ≠ kπ (k ∈ Z ) t = cotx a cot2 x + b cot x + c = 0 Nếu đặt: t = sin2 x hoaë t = sin x thì ñieà kieä : 0 ≤ t ≤ 1. c u n Baøi 1. Giải các phương trình sau: 1) 2sin2x + 5cosx + 1 = 0 2) 4sin2x – 4cosx – 1 = 0 4) tan2 x + ( 1− 3) tan x − 3 = 0 3) 4cos5x.sinx – 4sin5x.cosx = sin24x 5) 4sin2 x − 2( 3 + 1) sin x + 3 = 0 6) 4cos3 x + 3 2sin2x = 8cos x Vũ Hoang Anh-0984960096 ̀
- Bai tâp môt số phương trinh lượng giac thường găp ̣̀ ̣ ̀ ́ ̣ 7) tan2x + cot2x = 2 8) cot22x – 4cot2x + 3 = 0 Baøi 2. Giải các phương trình sau: 1) 4sin23x + 2( 3 + 1) cos3x − 3 = 4 2) cos2x + 9cosx + 5 = 0 − ( 3+ 3) tan x − 3+ 3 = 0 1 3) 4cos2(2 – 6x) + 16cos2(1 – 3x) = 13 4) 2 cos x 4 3 + tan2x = 9 5) 6) 9 – 13cosx + =0 1+ tan2 x cos x 1 1 + 3cot2x = 5 7) = cotx + 3 8) sin2 x 2 cos x 4 x 9) cos2x – 3cosx = 4cos2 10) 2cos2x + tanx = 2 5 sin3x + cos3x 3+ cos2x sin x + ÷= Baøi 3. Cho phương trình . Tìm các nghiệm của phương trình 1+ 2sin2x 5 thuộc ( 0 ; 2π ) . Baøi 4. Cho phương trình : cos5x.cosx = cos4x.cos2x + 3cos2x + 1. Tìm các nghi ệm c ủa ph ương trình thuộc ( −π ; π ) . π π 5 4 4 4 Baøi 5. Giải phương trình : sin x + sin x + ÷+ sin x − ÷ = . 4 4 4 III. PHƯƠNG TRÌNH BẬC NHẤT THEO SINX VÀ COSX DẠNG: a sinx + b cosx = c (1) Cách 1: • a2 + b2 ta được: Chia hai vế phương trình cho a b c sin x + cos x = (1) ⇔ a 2 + b2 a2 + b2 a 2 + b2 a b ( α ∈ 0, 2π ) Đặt: sinα = , cosα = • a2 + b 2 a2 + b2 c sinα .sin x + cosα .cos x = phương trình trở thành: a2 + b 2 c ⇔ cos(x − α ) = = cosβ (2) a2 + b2 • Điều kiện để phương trình có nghiệm là: c ≤ 1 ⇔ a2 + b2 ≥ c 2. 2 2 a +b • (2) ⇔ x = α ± β + k 2π (k ∈ Z ) Cách 2: xπ a/ Xét x = π + k 2π ⇔ = + kπ có là nghiệm hay không? 22 x b/ Xét x ≠ π + k 2π ⇔ cos ≠ 0. 2 Vũ Hoang Anh-0984960096 ̀
- Bai tâp môt số phương trinh lượng giac thường găp ̣̀ ̣ ̀ ́ ̣ 1− t 2 2t x Đặt: t = tan , thay sin x = , cos x = , ta được phương trình bậc hai theo t: 1+ t 2 1+ t 2 2 (b + c )t 2 − 2at + c − b = 0 (3) Vì x ≠ π + k 2π ⇔ b + c ≠ 0, nên (3) có nghiệm khi: ∆ ' = a2 − (c 2 − b2) ≥ 0 ⇔ a2 + b2 ≥ c 2. x =t . Giải (3), với mỗi nghiệm t0, ta có phương trình: tan 20 Ghi chú: 1/ Cách 2 thường dùng để giải và biện luận. 2/ Cho dù cách 1 hay cách 2 thì điều kiện để phương trình có nghiệm: a2 + b2 ≥ c 2. 3/ Bất đẳng thức B.C.S: y = a.sin x + b.cos x ≤ a 2 + b 2 . sin2 x + cos2 x = a 2 + b2 sin x cos x a ⇔ min y = − a2 + b2 vaømax y = a2 + b2 ⇔ = ⇔ tan x = a b b Baøi 1. Giải các phương trình sau: 6 2) sin x + cos x = 1) cos x + 3sin x = 2 3) 3 cos3x + sin3x = 2 2 ( 3 − 1) sin x − ( 3 + 1) cos x + 3 − 1= 0 4) sin x + cos x = 2sin5x 5) π 6) 3sin2x + sin + 2x ÷ = 1 2 Baøi 2. Giải các phương trình sau: 2) sin8x − cos6x = 3( sin6x + cos8x ) 1) 2sin2 x + 3sin2x = 3 π 3 1 4) cosx – 3sin x = 2cos − x ÷ 3) 8cos x = + 3 sin x cos x 2 5) sin5x + cos5x = 2 cos13x 6) (3cosx – 4sinx – 6) + 2 = – 3(3cosx – 4sinx – 6) Baøi 3. Giải các phương trình sau: 1) 3sinx – 2cosx = 2 2) 3 cosx + 4sinx – 3 = 0 3) cosx + 4sinx = –1 4) 2sinx – 5cosx = 5 Baøi 4. Giải các phương trình sau: π π 3 2 π 1) 2sin x + ÷ + sin x − ÷ = 2) 3 cos2x + sin2x + 2sin 2x − ÷ = 2 2 4 4 6 2 Baøi 5. Tìm m để phương trình : (m + 2)sinx + mcosx = 2 có nghiệm . Baøi 6. Tìm m để phương trình : (2m – 1)sinx + (m – 1)cosx = m – 3 vô nghiệm. IV. PHƯƠNG TRÌNH ĐẲNG CẤP BẬC HAI DẠNG: a sin2x + b sinx.cosx + c cos2x = d (1) Cách 1: • Kiểm tra cosx = 0 có thoả mãn hay không? π Lưu ý: cosx = 0 ⇔ x = + kπ ⇔ sin2 x = 1 ⇔ sin x = ± 1. 2 • Khi cos x ≠ 0 , chia hai vế phương trình (1) cho cos2 x ≠ 0 ta được: Vũ Hoang Anh-0984960096 ̀
- Bai tâp môt số phương trinh lượng giac thường găp ̣̀ ̣ ̀ ́ ̣ a.tan2 x + b.tan x + c = d (1+ tan2 x ) • Đặt: t = tanx, đưa về phương trình bậc hai theo t: (a − d )t 2 + b.t + c − d = 0 Cách 2: Dùng công thức hạ bậc 1− cos2x 1+ cos2x sin2x (1) ⇔ a. + b. + c. =d 2 2 2 ⇔ b.sin2x + (c − a).cos2x = 2d − a − c (đây là phương trình bậc nhất đối với sin2x và cos2x) Baøi 1. Giải các phương trình sau: 1) 2sin2 x + ( 1− 3) sin x.cos x + ( 1− 3) cos2 x = 1 2) 3sin2 x + 8sin x .cos x + ( 8 3 − 9) cos2 x = 0 3) 4sin2 x + 3 3sin x.cos x − 2cos2 x = 4 1 4) sin2 x + sin2x − 2cos2 x = 2 5) 2sin2 x ( 3+ 3) sin x.cos x + ( 3 − 1) cos2 x = −1 6) 5sin2 x + 2 3sin x.cos x + 3cos2 x = 2 7) 3sin2 x + 8sin x.cos x + 4cos2 x = 0 ( 2 − 1) sin2 x + sin2x + ( 2 + 1) cos2 x = 2 8) 9) ( 3 + 1) sin2 x − 2 3sin x.cos x + ( 3 − 1) cos2 x = 0 10) 3cos4 x − 4sin2 x cos2 x + sin4 x = 0 11) cos2x + 3sin2x + 2 3 sinx.cosx – 1 = 0 12) 2cos2x – 3sinx.cosx + sin2x = 0 Baøi 2. Giải các phương trình sau: 2 −1 3sin x.cos x − sin2 x = 1) sin3x + 2sin2x.cos2x – 3cos3x = 0 2) 2 Baøi 3. Tìm m để phương trình : (m + 1)sin x – sin2x + 2cos x = 1 có nghiệm. 2 2 Baøi 4. Tìm m để phương trình : (3m – 2)sin2x – (5m – 2)sin2x + 3(2m + 1)cos2x = 0 vô nghiệm . Vũ Hoang Anh-0984960096 ̀

CÓ THỂ BẠN MUỐN DOWNLOAD
-

Bài giảng Đại số 11 chương 1 bài 3: Một số phương trình lượng giác thường gặp
 16 p |
16 p |  2384
|
2384
|  1386
1386
-
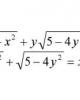
Bài tập Toán: Hệ phương trình
 31 p |
31 p |  947
|
947
|  217
217
-

Giáo trình toán học - hệ phương trình chứa căn thức - mũ và lôgarit
 1 p |
1 p |  959
|
959
|  177
177
-

Tổng hợp các phương pháp giải bài tập Toán học Phương trình và hệ phương trình - Nguyễn Văn Huy
 382 p |
382 p |  682
|
682
|  145
145
-

Một vài bài tập hay về phương trình vô tỷ - TS. Nguyễn Phú Khánh
 10 p |
10 p |  609
|
609
|  96
96
-

Một số phương pháp giải hệ phương trình - Nguyễn Minh Hiền
 3 p |
3 p |  217
|
217
|  36
36
-

Bài giảng Công nghệ 7 bài 33: Một số phương pháp chọn lọc và quản lí giống vật nuôi
 19 p |
19 p |  312
|
312
|  24
24
-

350 Bài tập trắc nghiệm phương trình lượng giác
 48 p |
48 p |  173
|
173
|  19
19
-

Một số phương trình biến đổi về phương trình bậc nhất với Sinx và Cosx
 4 p |
4 p |  231
|
231
|  17
17
-

Một số bài tập về hệ phương trình và phương pháp thế
 10 p |
10 p |  117
|
117
|  12
12
-

Sáng kiến kinh nghiệm: Hướng dẫn học sinh phương pháp giải một số dạng bài tập tính số nhiễm sắc thể lưỡng bội của loài trong Sinh học 9
 24 p |
24 p |  116
|
116
|  10
10
-

Giải bài tập Một số phương trình lượng giác thường gặp SGK Đại số và giải tích lớp 11
 7 p |
7 p |  199
|
199
|  6
6
-

Bài giảng Toán 11: Một số phương trình lượng giác thường gặp
 16 p |
16 p |  95
|
95
|  6
6
-

Giáo án Đại số lớp 11: Chuyên đề - Một số phương trình lượng giác thường gặp
 36 p |
36 p |  20
|
20
|  4
4
-

Bài giảng Hình học lớp 11 bài 3: Một số phương trình lượng giác thường gặp (Tiếp theo) - Trường THPT Bình Chánh
 8 p |
8 p |  34
|
34
|  4
4
-

Bài giảng môn Toán: Một số phương trình lượng giác thường gặp
 13 p |
13 p |  20
|
20
|  3
3
-

Sáng kiến kinh nghiệm: Một số dạng bài tập trắc nghiệm phương trình đường tròn
 18 p |
18 p |  77
|
77
|  1
1
Chịu trách nhiệm nội dung:
Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA
LIÊN HỆ
Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM
Hotline: 093 303 0098
Email: support@tailieu.vn









