Phòng Giáo D c Cam Lâmụ HSG Toán 9
CHUYÊN Đ PH NG TRÌNH, H PH NG TRÌNHỀ ƯƠ Ệ ƯƠ
A. Gi i ph ng trình b ng cách đt n ph thích h p.ả ươ ằ ặ ẩ ụ ợ
Bài 1:Gpt:
2 2 2
2
2 2 4
10. 11. 0.
1 1 1
x x x
x x x
− + −
� �
� � � �
+ − =
� � � � � �
+ − −
� � � � � �
Gi i:ả
Đt ặ
2 2
;
1 1
x x
u v
x x
− +
= =
+ −
(1).
Ta có: 10.u2 + v2 -11.uv = 0
(u-v).(10u-v)=0
u=v ho c 10u=v.ặ
Xét các tr ng h p thay vào (1) ta tìm đc x m t cách d dàng.ườ ợ ượ ộ ễ
Bài 2:Gpt: (x2 - 4x+3).(x2 - 6x + 8)=15.
Gi i:ả
Đt xặ2 - 5x + 5 = u (1).
Ta có: (x2 - 4x+3).(x2 - 6x + 8)=15
(x-1).(x-3).(x-2).(x-4)-15=0
(x-1).(x-2).(x-3).(x-4)-15=0
(x2-5x+4).(x2-5x+6)-15=0
(u-1).(u+1)-15=0
u2-16=0
u=
4.
Thay các giá tr c a u vào (1) ta d dàng tìm đc x.ị ủ ễ ượ
Bài 3:Gpt:
2
90.
1 1
x x
x x
� � � �
+ =
� � � �
+ −
� � � �
Gi i:ảPT
2
2 2
1 1
. 90
( 1) ( 1)
xx x
� �
+ =
� �
+ −
� �
.
2
2
2 2
2 2
. 90
( 1)
x
xx
+=�−
.
Đt u = xặ2 ( u
0) (1).
Ta có:
( u
1).
09018288 2 uu
.
T đây ta d dàng tìm đc u, thay vào (1) ta tìm đc x.ừ ễ ượ ượ
Bài 4:Gpt:
3 3 3
2 3 12.( 1)x x x+ − = −
.
Gi i:ả
1
Phòng Giáo D c Cam Lâmụ HSG Toán 9
Đt ặ
3 3
; 2 3x u x v= − =
(1).
Có:
).(4).(3).(4 3333
333 vuvuuvvuvuvu
vu
vu
vuvuvuvuvu 0)).(.(30)2).(.(3 222
Xét các tr ng h p thay vào (1) ta d dàng tìm đc x.ườ ợ ễ ượ
Bài 5:Gpt:
x
x
xxx 3
22
1
2335
2
23
(1).
Gi i:ả
T (1) suy ra: ừ
162335.2 223 xxxxx
xxxxxxxx 122121368121220 232423
0924228 234 xxxx
(x
0).
0
924
228 2
2 x
x
xx
.
Đt ặ
y
x
x 3
(*) ta có:
y2 - 8y + 16 = 0 suy ra y = 4 thay vào (*) ta d dàng tìm đc x.ễ ượ
Bài 6:Gpt:
).1(018
4
1
).4.(3)4.(1
x
x
xxx
Gi i: ảĐi u ki n x > 4 ho c x < -1.ề ệ ặ
*N u x > 4, (1) tr thành:ế ở
018)4).(1(.3)4).(1( xxxx
Đt ặ
0)4).(1( yxx
(2) ta có:
y2 + 3y -18 = 0.
T đó ta d dàng tìm đc y,thay vào (2) ta tìm đc x.ừ ễ ượ ượ
*N u x < -1, (1) tr thành:ế ở
018)4).(1(.3)4).(1( xxxx
Đt ặ
0)4).(1( yxx
(3) ta có:
y2 - 3y -18 = 0.
T đó ta d dàng tìm đc y,thay vào (3) ta tìm đc x.ừ ễ ượ ượ
Bài 7 Gpt:(2x2 - 3x +1).(2x2 + 5x + 1)=9x2 (1).
Gi i:ả
(1)
0122044 234 xxxx
(x
0).Chia c hai v cho xả ế 2 ta đc :ượ
4x2 + 4x -20 +
2
12
x
x
= 0.
024
1
2.2
1
2
2
x
x
x
x
. Đt y = ặ
x
x1
2
.(2)
Ta có: y2 + 2y -24 = 0.
T đó ta tìm đc y,thay vào (2) ta d dàng tìm đc x.ừ ượ ễ ượ
2
Phòng Giáo D c Cam Lâmụ HSG Toán 9
Bài 8:Gpt:
.0168.26416 222 xxxxx
Gi i:ảPT
.04.28 xxx
Đn đây ta xét t ng kho ng ,bài toán tr nên đn gi n.ế ừ ả ở ơ ả
Bài 9:Gpt: (1 + x + x2)2 = 5.(1 + x2 + x4).
Gi i:ả
423242 5552221 xxxxxxx
4 3 2 4 3 2
4 2 2 2 4 0 2 2 0x x x x x x x x− + − + = − + − + =� �
Nh n th y x = 0 không ph i là nghi m c a ph ng trình đã cho, v y xậ ấ ả ệ ủ ươ ậ
0.
Chia c hai v c a ph ng trình trên cho xả ế ủ ươ 2 ta đc:ượ
2x2 - x + 1 -
0
21
2 x
x
. Đt y = ặ
x
x1
(*). Ta có:
2y2 - y - 3 = 0.T đó ta d dàng tìm đc y, thay vào (*) ta tìm đc x.ừ ễ ượ ượ
Bài 10: Gpt: (6-x)4 + (8-x)4 = 16.
Gi i:ả
Đt 7 - x = y (*).ặ
Ta có: (y-1)4 + (y + 1)4 =16
2y4 +12 y2 +2 = 16
2.(y-1).(y+1).(y2+7)=0
y =1 ho c y = -1.ặ
Thay các giá tr c a y tìm đc trên thay vào (*) ta d dàng tìm đc các giá tr c a x.ị ủ ượ ở ễ ượ ị ủ
Tìm các nghi m nguyên (x;y) ho c (x;y;z) c a các ph ng trình sau:ệ ặ ủ ươ
Bài 1: x2 = y.(y+1).(y+2).(y+3)
Gi i:ả
Đt yặ2 + 3y = t.
Ta có: x2 = y.(y+1).(y+2).(y+3) = (y2 + 3y).(y2 + 3y +2) = t2 + 2t.
*N u t > 0 thì tế2 < x2 = t2 + 2t < (t+1)2 suy ra không t n t i x th a mãn.ồ ạ ỏ
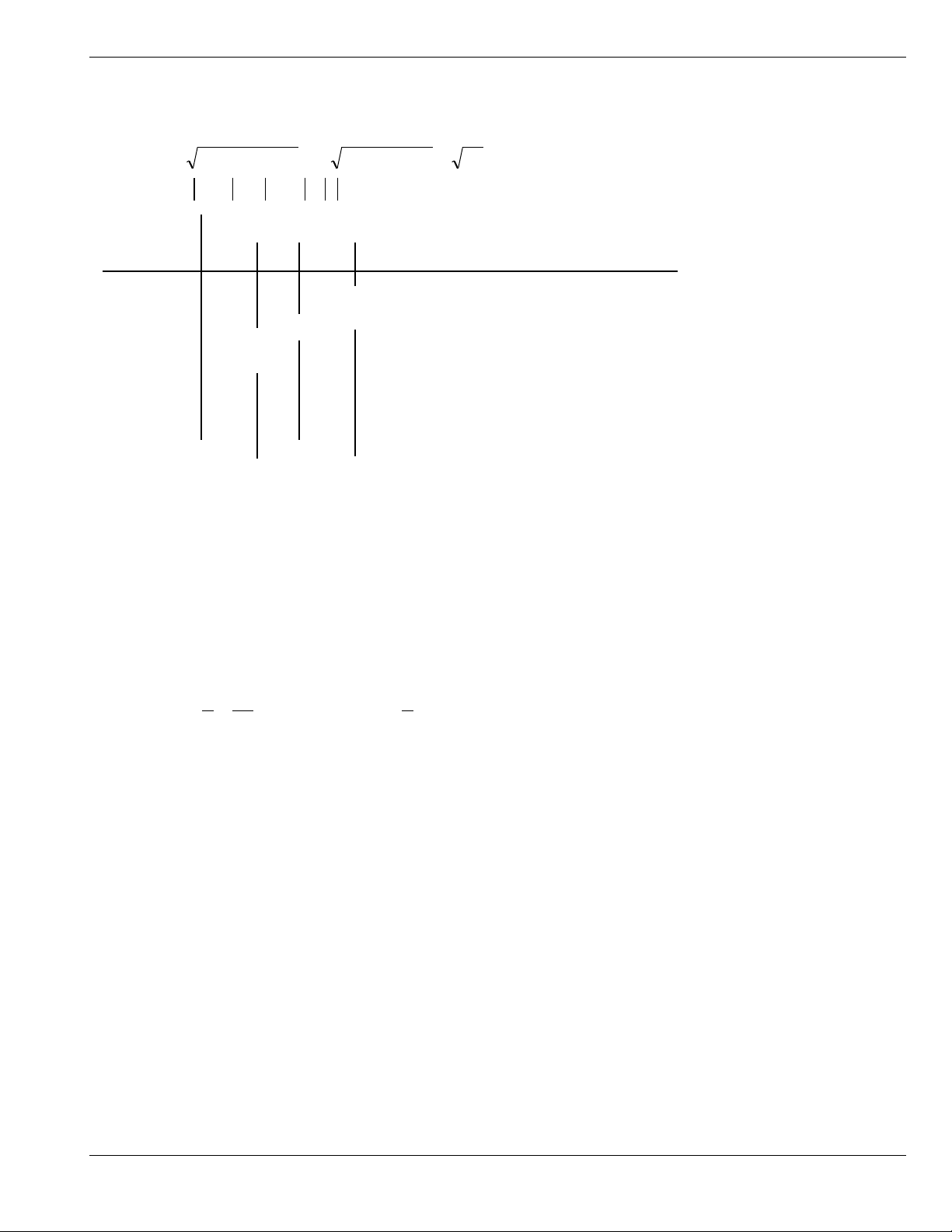
3
x - 0 4 8 +
x-8 - - - 0 +
x-4 - - 0 + +
x - 0 + + +
Phòng Giáo D c Cam Lâmụ HSG Toán 9
*N u t < -2 thì 2t + 4 < 0 nên tế2 + 2t > t2 + 4t + 4 suy ra t2 + 2t > t2 + 4t + 4 = (t+2)2.
Suy ra: x2 = t2 + 2t > (t + 2)2 (*).
L i có: tạ2 +2t < t2 suy ra x2 < t2 (**).
T (*)&(**) suy ra (t + 2)ừ2 < x2 < t2 suy ra x2 = (t+1)2 suy ra t2 +2t = (t +1)2 (=x2)
Suy ra : t2 +2t = t2 +2t +1 (Vô lý).
*N u t = -1 suy ra xế2 = t2 +2t = -1 <0 (Vô lý).
*N u t = 0 suy ra x = 0ế
y = 0 ho c -1 ho c -2 ho c -3 .ặ ặ ặ
Bài 2:
2
2 (1)
2 2 1 (2)
x y z
x xy x z
− + =
− + − =
Gi i:ả
T (2) ta có: 2xừ2 - xy+x-2z =1 k t h p v i (1) ta có:ế ợ ớ
2x2 - xy+x-2.(2 - x + y)=1
2x2 -xy +3x-2y-5=0
.7,1227
2
7
1
2
53
2
xx
x
x
x
xx
y
T đó ta tìm đc x ừ ượ
tìm đc y ượ
tìm đc z.ượ
Bài 3:
)2(1
)1(3
222 zyx
zyx
Gi i: ảThay (1) vào (2) ta đc:ượ
(y + z -3)2 -y2 -z2 =1
yz - 3y - 3z = -4
(y-3).(z-3) = 5 = 1.5 = (-1).(-5) = 5.1=(-5).(-1.
T đó ta tìm đc y và z ừ ượ
tìm đc x.ượ
Bài 4: 2xy + x + y = 83.
Gi i:PTả
.167,11212167
12
167
1
12
2166
2
12
83
yy
yy
y
x
y
y
x
T đó ta tìm đc y ừ ượ
tìm đc x.ượ
Bài 5:
.3 y
zx
x
yz
z
xy
Gi i:ảĐi u ki n : x,y,z ề ệ
0.
Nh n xét:Trong ba s x,y,z luôn t n t i hai s cùng d u (Theo nguyên t c Đirichlê có 3 s ậ ố ồ ạ ố ấ ắ ố
-3 th mà ch có hai chu ng-m i s nguyên khác 0 ch mang d u âm ho c d u d ng)ỏ ỉ ồ ọ ố ỉ ấ ặ ấ ươ
Ta có th gi s x,y cùng d u v i nhau.Suy ra x.y =ể ả ử ấ ớ
xy
> 0 và
.0,
x
y
y
x
Đt A=ặ
.3 y
zx
x
yz
z
xy
Gi s z <0 khi đó 3 = A =ả ử
0000 y
zx
x
yz
z
xy
(Vô lý).
V y z >0.Ta có:ậ
4
Phòng Giáo D c Cam Lâmụ HSG Toán 9
A =
3
3.3.....3..3 zxy
x
y
z
y
x
z
z
xy
y
x
z
x
y
z
z
xy
y
zx
x
yz
z
xy
1,1
1,1
1,1.1 yxz
yxz
xyzzxy
Bài 6: 2x2 - 2xy = 5x + y - 19.
Gi i:ảT bài ra ta có:ừ
.17,1121217
12
17
2
12
1952 2
xx
x
x
x
xx
y
T đó ta tìm đc x ừ ượ
tìm đc y.ượ
B. Gi i h ph ng trình và các ph ng trình khác.ả ệ ươ ươ
Bài 1:
.2
2
11
2
x
x
Gi i:ảĐi u ki n :ề ệ
2,0 xx
.
-N u x < 0 thì ế
2
2
11
x
x
.2
2
1
2
1
2
x
V y ta xét x > 0:ậ
Đt x = a và ặ
bx 2
2
(a,b > 0).
Ta có:
2
2
11
22 ba
ba
Có:
1
1
.2
11
2 ab
abba
(1).
L i có: 2 = aạ2 + b2
2ab suy ra 1
ab (2).
T (1)&(2) suy ra ab = 1 mà aừ2 + b2 =2 nên suy ra (a+b)2 = 4 suy ra a + b = 2.
V y ta có:ậ
11
2
1
xba
ba
ab
.
Bài 2:
.51632414 4222 yxyyxxx
Gi i:ả
Đi u ki n:ề ệ
)4(016
)3(032
)2(041
)1(04
4
22
2
x
yyx
x
x
T (4) suy ra xừ2
4 k t h p v i (1) suy ra xế ợ ớ 2 = 4 k t h p v i (2) suy ra x = 2.ế ợ ớ
Ph ng trình đã cho tr thành:ươ ở
51 yy
.
Lúc này vi c tìm y không còn khó khăn gì n a (L p b ng xét d u).ệ ữ ậ ả ấ
Bài 3: 2x4 -21x3 + 74x2 -105x +50 =0.
5