
Chuyên đề : PHƯ Ơ NG TRÌNH LƯ Ợ NG GIÁC-Theo hư ớ ng ra đề thi củ a BỘ GIÁO DỤ C
DẠ Y ÔN LỚ P 11 và LUYỆ N THI ĐẠ I HỌ C 1 Nguyễ n Công Mậ u
LỜ I NÓI ĐẦ U:
Kính thư a các đồ ng nghiệ p cùng bạ n đọ c:
Tôi viế t chuyên đề giả i PTLG này nhằ m trao đổ i cùng đồ ng nghiệ p để tham khả o.
Bên cạ nh đó giúp cho các em họ c sinh đã họ c xong chư ơ ng trình THPT tự họ c để có thể
tự ôn luyệ n vào các trư ờ ng đạ i họ c theo nguyệ n vọ ng củ a mình.
Nế u nói mộ t chuyên đề PTLG thì phả i giớ i thiệ u tấ t cả các dạ ng phư ơ ng trình và
cách giả i hoặ c thuậ t toán củ a từ ng dạ ng.Tuy nhiên trong quá trình giả ng dạ y và nghiên
cứ u cách cho đề củ a các đề thi đạ i họ c từ nhữ ng năm gầ n đây bả n thân tôi rút ra đư ợ c
kinh nghiệ m:
+Số chuyên đề củ a mộ t họ c sinh phả i họ c quá nhiề u, do vậ y vấ n đề về thờ i gian
dành để ôn luyệ n cho mỗ i chuyên đề phả i đư ợ c tính đế n.
+Dạ y và ôn như thế nào để phù hợ p vớ i xu thế ra đề củ a Bộ Giáo dụ c.
Do vậ y tài liệ u này tôi đã tích lũy từ nhiề u năm, các bài tậ p đư ợ c biên soạ n chỉ
ngang tầ m vớ i các đề thi đạ i họ c đã diễ n ra hoặ c mứ c độ chênh lệ ch nhau không đáng
kể .Tài liệ u này đư ợ c viế t theo các nộ i dung chính say đây:
A.Ôn lý thuyế t:Không trình bày phầ n lý thuyế t nhằ m tránh tài liệ u quá dài.
B.Sơ đồ hệ thố ng cách giả i các phư ơ ng trình lư ợ ng giác trong các đề thi đạ i họ c.
(Sau mỗ i bài giả i hoặ c ví dụ ,bạ n hãy thử xem đố i chiế u lạ i vớ i sơ đồ !)
C.Ôn tậ p cách giả i các phư ơ ng trình thư ờ ng gặ p đã nâng cao.Trong phầ n này có ví
dụ và có lờ i giả i hoặ c hư ớ ng dẫ n cách giả i.Cuố i củ a mỗ i mụ c có phầ n bài tậ p hoàn toàn
tư ơ ng tự , do vậ y tôi không ghi cách giả i. Riêng phầ n PTLG đẳ ng cấ p bậ c n tôi đã biên
soạ n các ví dụ theo hai cách giả i để bạ n đọ c thấ y đư ợ c ư u điể m củ a mỗ i cách.Số bài tậ p
tư ơ ng tự mụ c này nhiề u hơ n so vớ i nhữ ng nộ i dung khác.
D.Phầ n bài tậ p để rèn luyệ n chung cho chuyên đề -phầ n này tôi biên soạ n tư ơ ng
ứ ng vớ i mứ c độ các đề thi đạ i họ c từ 2002-2009 . Các em họ c sinh có thể nghiên cứ u đáp
án các đề thi đạ i họ c từ 2002-2009 để giả i nó (nế u không giả i đư ợ c).(Nế u các em là họ c
sinh có yêu cầ u bài giả i phầ n này thì có thể liên hệ theo email:
maunguyencong@yahoo.com hoặ csố điệ n thoạ i: 0984-003114.
E.Nộ i dung các đề thi đạ i họ c các khố i từ 2003-2009 để dễ so sánh vớ i các bài tậ p ở
phầ n D.
F.Nghiên cứ u thêm nhữ ng gợ i ý về cách giả i các phư ơ ng trình lư ợ ng giác.
Tôi hy vọ ng rằ ng, nế u đọ c kỹ về cách giả i PTLG cùng vớ i sơ đồ hệ thố ng các em
họ c sinh có thể tự họ c tố t về chuyên đề này.
Chúc tấ t cả chúng ta thành công và cũng mong đồ ng nghiệ p và các em họ c sinh
thông cả m cho bả n thân tôi trong quá trình biên soạ n tài liệ u này không sao tránh khỏ i
nhữ ng sai sót. Chào thân ái!
A. ÔN LÝ THUYẾ T:
Ôn :giá trị lư ợ ng giác các góc đặ c biêt, giá trị lư ợ ng giác củ a các cung góc có
liên quan đặ c biêt. Các công thứ c cơ bả n, công thứ c lư ợ ng giác…
Ôn : Phư ơ ng trình lư ợ ng giác cơ bả n và cách giả i.
OÂN LUYỆ N PHÖÔNG TRÌNH LÖÔÏNG GIAÙC
Chuyên đề : PHƯ Ơ NG TRÌNH LƯ Ợ NG GIÁC-Theo hư ớ ng ra đề thi củ a BỘ GIÁO DỤ C
DẠ Y ÔN LỚ P 11 và LUYỆ N THI ĐẠ I HỌ C 2 Nguyễ n Công Mậ u
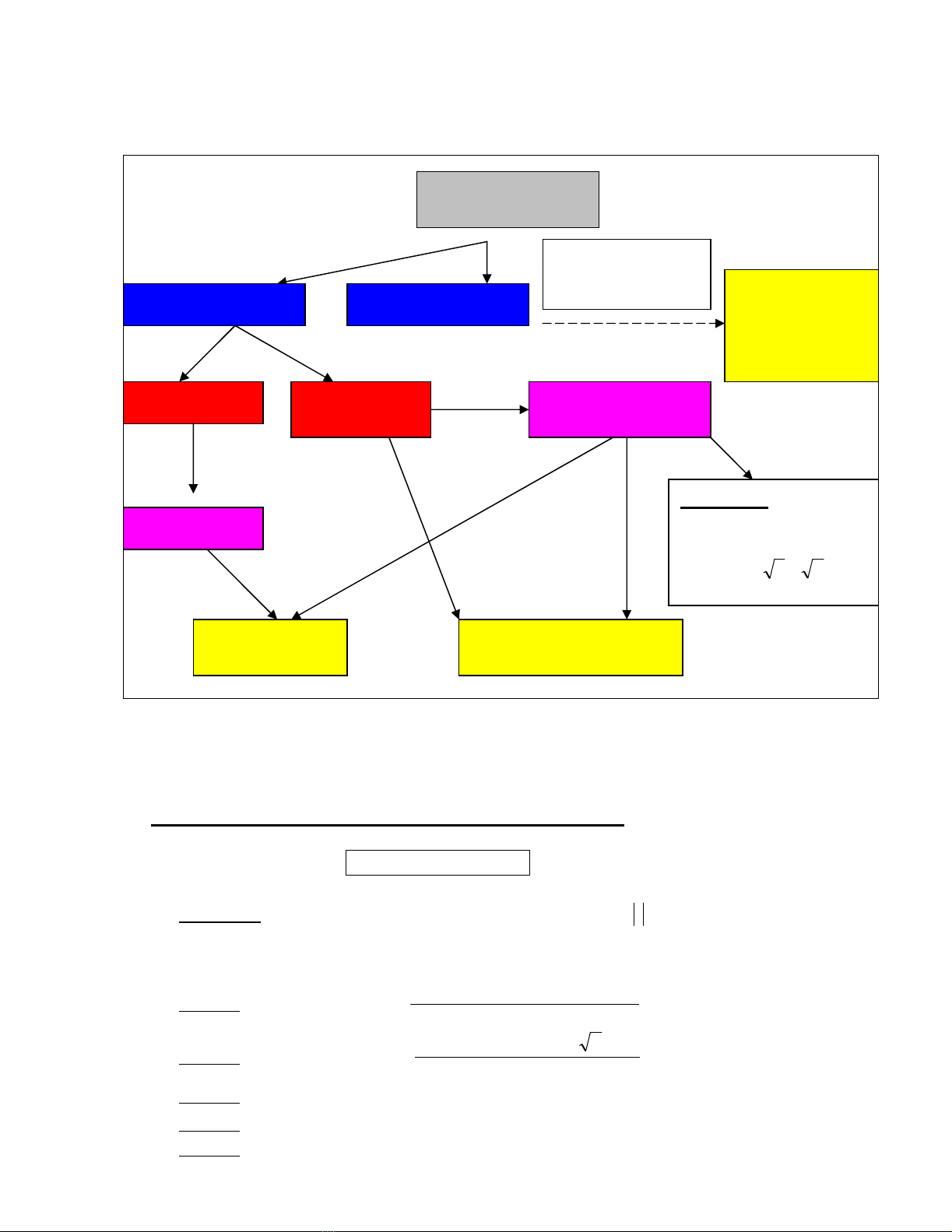
B. SƠ ĐỒ HỆ THỐ NG CÁCH GIẢ I CÁC PHƯ Ơ NG TRÌNH LƯ Ợ NG
GIÁC TRONG CÁC ĐỀ THI ĐẠ I HỌ C TỪ NĂM 2002- 2009.
(ẩ n phụ )
C.ÔN TẬ P CÁCH GIẢ I CÁC DẠ NG PHƯ Ơ NG TRÌNH THƯ Ờ NG GẶ P.
VÍ DỤ-CÁCH GIẢ I –GIẢ I HOẶ C HƯ Ớ NG DẪ N VÀ BÀI TẬ P.
I. Phư ơ ng trình bậ c hai đố i vớ i mộ t hàm số lư ơ ng giác:
Phư ơ ng trình dạ ng : a.f2(x) + b.f(x) + c = 0 , trong đó f(x) là hàm số lư ợ ng giác.
Và a, b, c là các hệ số a
0.
Cách giả i: + Đặ t = f(x) ( nế u f(x) là sinx hoặ c cosx thì
1t
)
+ Giả i phư ơ ng trình at2 + bt + c = 0 và chọ n t thoả mãn điề u kiệ n.
+ Giả i phư ơ ng trình f(x) = t.
Ví dụ 1) Giả i phư ơ ng trình :
2
2cos 4 6 s 1 3cos 2 0
cos
x co x x
x
(1)
Ví dụ 2) Giả i phư ơ ng trình :
1
cos1
sin2)1cos2(cos1
x
xxx
(2)
Ví dụ 3) Giả i phư ơ ng trình :
2
3 2 3(1 ).cotcosx cosx x
(3)
Ví dụ 4) Giả i phư ơ ng trình :
6 6 2
sin 2 1x cos x cos x
(4)
Ví dụ 5) Tìm các nghiệ m trên khoả ng
0;
củ a phư ơ ng trình :
PTLG cho trư ớ c
PT còn mộ t cung
Còn 1 HSLG
PTĐẠ I SỐ
Còn 2 hàm
sin và côsin
PTLG cơ bả n
PTLG THƯ Ờ NG GẶ P
PT còn hai cung
Áp dụ ng:
(asinu + bcosu)
PTcơ bả n
Sinf(x)=sing(x)
Hoặ c
cosf(x)=cosg(x)
P.T.Tích
Cầ n chú ý sự xuấ t
hiệ n các biể u thứ c:
a.sinx +b.cosx vớ i:
a,b =
2;3;1

Chuyên đề : PHƯ Ơ NG TRÌNH LƯ Ợ NG GIÁC-Theo hư ớ ng ra đề thi củ a BỘ GIÁO DỤ C
DẠ Y ÔN LỚ P 11 và LUYỆ N THI ĐẠ I HỌ C 3 Nguyễ n Công Mậ u
sin 3 cos3
7 4 cos 2
2sin 2 1
x x cosx x
x
(5)
Ví dụ 6) Cho phư ơ ng trình :
cos 2 (2 1)sin 1 0 (*)x m x m
.
a) Giả i phư ơ ng trình khi m = 2.
b) Tìm m để phư ơ ng trình (*) có nghiệ m trên khoả ng
;2
.
HƯ Ớ NG DẪ N GIẢ I CÁC VÍ DỤ :
Ví dụ 1) +Đk
mx 2
.
(1)
02cos312cos1(312cos22
2
xxx
kx
k
x
x
x
xx
6
2
2
1
2cos
12cos
012cos32cos2 2
Họ
2
k
x
thỏ a ĐK khi k = 2h
hx
Vậ y (1) có 3 họ nghiệ m là:
Zkhkxhx ,;
6
;
.
Ví dụ 2) + ĐK :
21cos mxx
(2)
0sin2)sin1(2cos1sin2coscos21 22 xxxxxx
2sin
2
2
sin02sin2sin2 2 xxxx
(loạ i)
2
4
5
2
4
4
sin
2
2
sin
kx
kx
x
Ví dụ 3) +ĐK :
mx
(3)
x
x
xx 2
2
sin
cos
)cos1(322cos3
x
x
xx 2
2
cos1
cos
)cos1(322cos3
02coscos6
cos1
cos3
2cos3 2
2
xx
x
x
x
2)
3
2
arccos(
2
3
3
2
cos
2
1
cos
kx
kx
x
x
(Thỏ a các ĐK)
Ví dụ 4) +Biế n đổ i:
4
1
2cos
4
3
2sin
4
3
1)cos(sincossin3)cos(sin
)(cossincossin
2
22222322
32
3
266
x
xxxxxxx
xxxx
(4)
012cos42cos32cos
4
1
2cos
4
322 xxxx

Chuyên đề : PHƯ Ơ NG TRÌNH LƯ Ợ NG GIÁC-Theo hư ớ ng ra đề thi củ a BỘ GIÁO DỤ C
DẠ Y ÔN LỚ P 11 và LUYỆ N THI ĐẠ I HỌ C 4 Nguyễ n Công Mậ u
2
3
1
arccos
2
1
3
1
2cos
12cos
kx
kx
x
x
Ví dụ 5) *Giả i PT(5):
+ĐK : sinx
2
12
2
12
5
2
1
mx
mx
+Ta có
)cossin1)(cos(sin4)cos(sin3cos3cos4sin4sin33cos3sin 33 xxxxxxxxxxxx
)12sin2)(cos(sin)1cossin4)(cos(sin xxxxxxx
xx
x
xx cossin
12sin2
3cos3sin
(5)
)sin21(4sin72cos4)coscos(sin7 2xxxxxx
3sin
2
1
sin03sin7sin2 2 xxxx
(loạ i)
2
6
5
2
6
2
1
sin
kx
kx
x
*Chọ n nghiệ m trên khoả ng
;0
ta đư ợ c hai nghiệ m củ a phư ơ ng trình là:
6
5
;
6
xx
Ví dụ 6) (*)
01sin)12(sin21 2 mxmx
0sin)12(sin2 2 mxmx
1;1;sin;0)12(2)( 2 txtmtmttf
a)Khi m=2:
2
2
1
0252)( 2 tttttf
(loạ i)
2
6
5
2
6
2
1
sin
2
1
kx
kx
xt
b)Tìm m để PT (*) có nghiệ m trên khoả ng
;2
:
Khi
012; tx
.
Vậ y ta phả i có :
01
0)1(0)1().0(
0
2
1
0)1(;0)0(;0
01
01
01
21
21
21
m
m
fff
S
afaf
tt
tt
tt
0;1 m
BÀI TẬ P TƯ Ơ NG TỰ :

Chuyên đề : PHƯ Ơ NG TRÌNH LƯ Ợ NG GIÁC-Theo hư ớ ng ra đề thi củ a BỘ GIÁO DỤ C
DẠ Y ÔN LỚ P 11 và LUYỆ N THI ĐẠ I HỌ C 5 Nguyễ n Công Mậ u
1) Giả i phư ơ ng trình :
2 2
4sin 2 6sin 9 3cos 2 0
cos
x x x
x
2) Giả i phư ơ ng trình :
2
cos 2 3 2 2 1
1
1 sin 2
x sinx cos x
x
3) Giả i phư ơ ng trình :
2
5 2 3(1 ).tansinx sinx x
4) Giả i phư ơ ng trình :
8 8 2
17
sin 2
16
x cos x cos x
5 Tìm các nghiệ m trên khoả ng
0;2
củ a phư ơ ng trình :
cos3 sin 3
5 3 cos 2
1 2sin 2
x x
sinx x
x
6) Cho phư ơ ng trình :
cos 2 (2 1) cos 1 0 (*)x m x m
.
a) Giả i phư ơ ng trình khi m = 3/2.
b) Tìm m để phư ơ ng trình (*) có nghiệ m trên khoả ng
3
;
2 2
.
II. Phư ơ ng trình bậ c nhấ t theo sin và côsin cùng mộ t cung:
Phư ơ ng trình dạ ng : asinx + bcosx = c , vớ i a.b
0
+ Điề u kiệ n phư ơ ng trình có nghiệ m : a2 + b2
c2.
+ Cách giả i :
- Chia 2 vế phư ơ ng trình cho
2 2
a b
ta đư ợ c :
2 2 2 2 2 2
cosasinx b x c
a b a b a b
-Đặ t
2 2 2 2
sin
a b
cos
a b a b
và đặ t
2 2
sin c
a b
ta có phư ơ ng trình:
sin( ) sinx
Ví dụ 1: Giả i phư ơ ng trình :
xxxx 2cos34cos26sin32cos4 3
(1)
Ví dụ 2: Giả i phư ơ ng trình :
3 1
8sinx cosx sinx
(2)
Ví dụ 3: Giả i phư ơ ng trình :
0sincos2cos2sin xxxx
(3)
Ví dụ 4: Giả i phư ơ ng trình :
82cos2sin3cos3sin9 xxxx
(4)
Ví dụ 5: Giả i phư ơ ng trình :
3
2 cos 2 0cos x x sinx
(5)
Ví dụ 6: Giả i phư ơ ng trình :
3 3
sin x cos x sinx cosx
(6)
Ví dụ 7: Giả i phư ơ ng trình : 4
4 4
(sin ) 3 sin 4 2x cos x x
(7)
Ví dụ 8: Giả i phư ơ ng trình :
xxxx sin3cos)cos3(sin3
(8)
HƯ Ớ NG DẪ N GIẢ I CÁC VÍ DỤ :
Ví dụ 1: (1)
xxxx 4cos26sin32cos32cos4 3
xxxxxx 4cos6sin
2
3
6cos
2
1
4cos26sin36cos
xx 4cos
3
6cos
.


























