TOÁN 11-CHÂN TRỜI SÁNG TẠO
Trang 1
PHẦN A. LÝ THUYẾT VÀ VÍ DỤ MINH HỌA
1. Hàm số lượng giác
Hàm số
sin
là quy tắc đặt tương ứng mỗi số thực
x
với số thực
sin x
, kí hiệu
siny x
.
Hàm số côsin là quy tắc đặt tương ứng mỗi số thực
x
với số thực
cos x
, kí hiệu
cosy x
.
Hàm số tang là hàm số được xác định bởi công thức
sin
; ( ),
cos 2
x
y x k k
x
kí hiệu tany x
Hàm số côtang là hàm số được xác định bởi công thức
cos ; ( ),
sin
x
y x k k
x
kí hiệu cot . y x
Như vậy:
- Tập xác định của hàm số
siny x
và
cosy x
là
.
- Tập xác định của hàm số tany x là \2
D k k
.
- Tập xác định của hàm số coty x là
\{ }D k k
.
2. Hàm số chẵn, hàm số lẻ, hàm số tuần hoàn
Hàm số chẵn, hàm số lẻ
- Hàm số
( )y f x
với tập xác định
D
được gọi là hàm số chẵn nếu với mọi
x D
ta có
x D
và
( ) ( )f x f x
.
- Hàm số
( )y f x
với tập xác định
D
được gọi là hàm số lẻ nếu với mọi
x D
ta có
x D
và
( ) ( )f x f x
.
Chú ý: Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
Đồ thị của hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
Ví dụ 1. Xét tính chẵn, lẻ của các hàm số lượng giác cos , tany x y x .
Giải
a) Hàm số
cosy x
có tập xác định là
. Với mọi
x
ta có
x
và
cos( ) cosx x
.
Do đó hàm số
cosy x
là hàm số chẵn.
b) Hàm số tany x có tập xác định là \ 2k k
.
Với mọi
( )
2
x k k
ta có
( )
2
x k k
, cũng có nghĩa là
( )
2
x k k
hay \ 2
x k k
.
Mặt khác
tan( ) tanx x
. Do đó hàm số tany x là hàm số lẻ.
Hàm số tuần hoàn
Hàm số
( )y f x
với tập xác định
D
được gọi là hàm số tuần hoàn nếu tồn tại một số
T
khác 0
sao cho với mọi
x D
ta có
x T D
và
( ) ( )f x T f x
.
Số
T
dương nhỏ nhất thoả mãn các điều kiện trên (nếu có) được gọi là chu kì của hàm số tuần
hoàn
( )y f x
.
Chú ý: Đồ thị của hàm số tuần hoàn chu kì
T
được lặp lại trên từng đoạn giá trị của
x
có độ dài
T
.
Ví dụ 2. Xét tính tuần hoàn của hàm số
siny x
và hàm số tany x.
Giải
BÀI 4. HÀM SỐ LƯỢNG GIÁC VÀ ĐỒ THỊ
•CHƯƠNG 1. HÀM SỐ LƯỢNG GIÁC VÀ PHƯƠNG TRÌNH LƯỢNG GIÁC
•|FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2
Ta có:
sin sin( 2 )x x
với mọi
x
;
tan( ) tan , , .
2
x x x k k
Do đó hàm số
siny x
và tany x là các hàm số tuần hoàn.
Chú ý: Người ta chứng minh được rằng:
a) Các hàm số
siny x
và
cosy x
là các hàm số tuần hoàn với chu kì
2
;
b) Các hàm số tany x và coty x là các hàm số tuần hoàn với chu kì
.
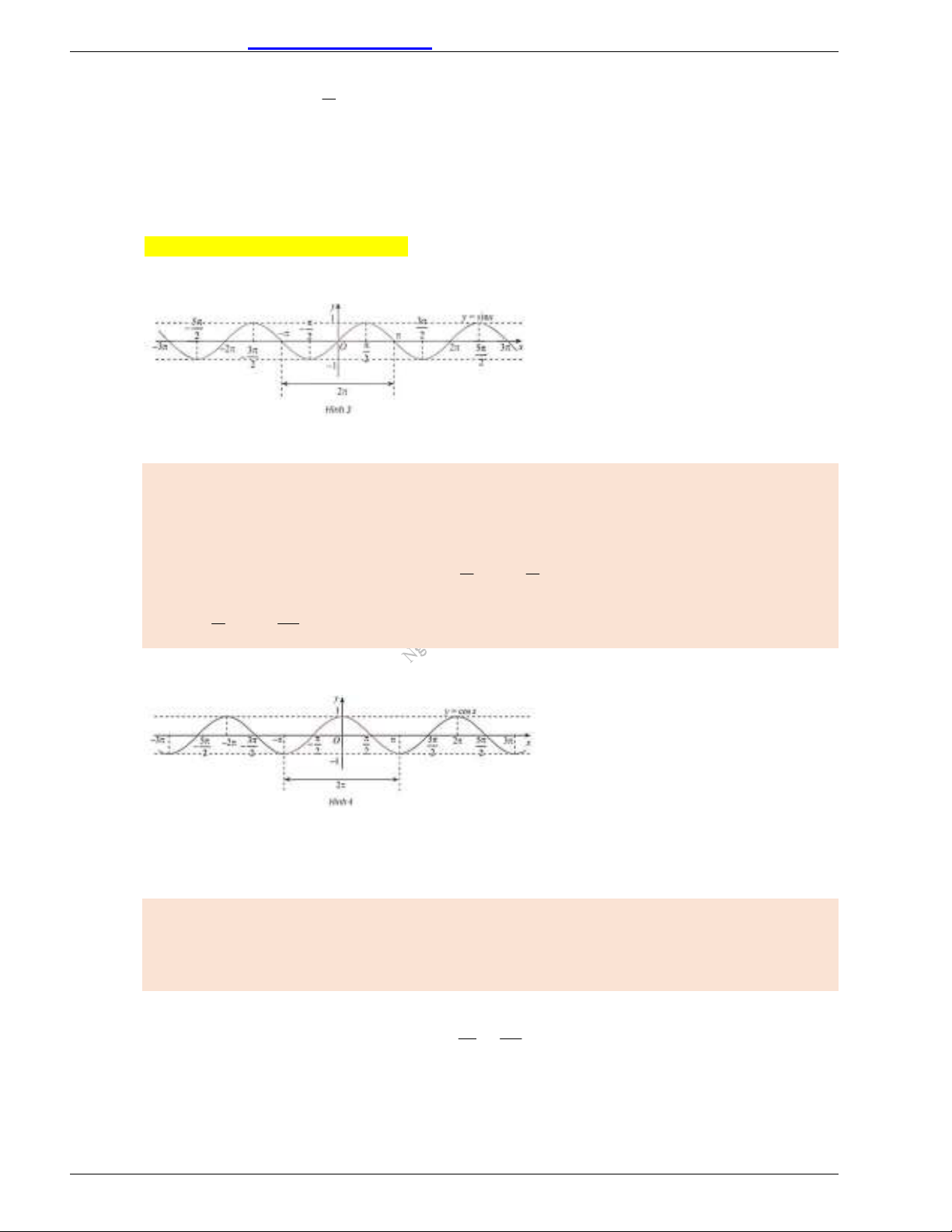
3. Đồ thị của các hàm số lượng giác
Hàm số
siny x
Ta có đồ thị của hàm số
siny x
trên
như sau:
Chú ý: Vì
siny x
là hàm số lẻ nên để vẽ đồ thị của nó trên đoạn
[ ; ]
, ta có thể vẽ trên đoạn
[0; ]
, sau đó lấy đối xứng qua gốc toạ độ.
Từ đồ thị trên, ta thấy hàm số
siny x
có tập xác định là
, tập giá trị là
[ 1;1]
và có các tính
chất sau:
- Hàm số tuần hoàn với chu kì
2
.
- Hàm số lẻ, có đồ thị đối xứng qua gốc toạ độ
O
.
- Hàm số đồng biến trên các khoảng
2 ; 2 ( )
2 2
k k k
và nghịch biến trên các
khoảng
3
2 ; 2 ( )
2 2
k k k
.
Hàm số
cosy x
Ta có đồ thị của hàm số
cosy x
trên
như sau:
Chú ý: Vì
cosy x
là hàm số chẵn nên để vẽ đồ thị của nó trên đoạn
[ ; ]
, ta có thể vẽ trên
đoạn
[0; ]
, sau đó lấy đối xứng qua trục tung.
Từ đồ thị trên, ta thấy hàm số
cosy x
có tập xác định là
, tập giá trị là
[ 1;1]
và có các tính
chất sau:
- Hàm số tuần hoàn với chu kì
2
.
- Hàm số chẵn, có đồ thị đối xứng qua trục
Oy
.
- Hàm số đồng biến trên các khoảng
( 2 ; 2 )( )k k k
và nghịch biến trên các khoảng
( 2 ; 2 )( )k k k
.
Ví dụ 3. Nhiệt độ ngoài trời
T
(tính bằng
C
) vào thời điểm
t
giờ trong một ngày ở một thành
phố được tính bởi công thức
5
20 4sin 12 6
T t
. Để bảo quản các tác phẩm nghệ thuật, hệ
thống điều hoà nhiệt độ của một bảo tàng sẽ được tự động bật khi nhiệt độ ngoài trời từ
22 C
trở
lên. Dựa vào đồ thị của hàm số
sin
, hãy xác định khoảng thời gian
t
trong ngày
(0 24)t
hệ
thống điều hoà được bật.
(Theo https://www.sciencedirect.com/science/article/abs/pii/0168192385900139)
Giải
TOÁN 11-CHÂN TRỜI SÁNG TẠO
Trang 3
Ta có
22T
khi và chi khi
5
20 4sin 22
12 6
t
hay
5 1
sin 12 6 2
t
. Vì
0 24t
nên
5 5 7
6 12 6 6
t
.
Xét đồ thị hàm số
siny x
trên đoạn
5 7
;
6 6
(Hình 5).
Ta thấy
5 1
sin 12 6 2
t
khi và chỉ khi
5 5
6 12 6 6
t
hay
12 20t
.
Vậy hệ thống điều hoà được bật trong khoảng thời gian từ 12 giờ đến 20 giờ trong ngày.
Hàm số tany x
Ta có đồ thị của hàm số tany x trên
\2k k
như sau:
Chú ý: Vì tany x là hàm số lẻ nên để vẽ đồ thị của nó trên khoảng
;
2 2
, ta có thể vẽ trên
nửa khoảng
0; 2
, sau đó lấy đối xứng qua gốc toạ độ.
Từ đồ thị trên, ta thấy hàm số tany x có tập xác định là
\2k k
, tập giá trị là
và
có các tính chất sau:
- Hàm số tuần hoàn với chu kì
.
- Hàm số lẻ, có đồ thị đối xứng qua gốc toạ độ
O
.
- Hàm số đồng biến trên các khoàng
; ( )
2 2
k k k
.
Hàm số coty x
Ta có đồ thị của hàm số coty x trên
\{ }k k
như sau:
Từ đồ thị trên, ta thấy hàm số coty x có tập xác định là
\{ }k k
, tập giá trị là
và có
các tính chất sau:
- Hàm số tuần hoàn với chu kì
.
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
- Hàm số lẻ, có đồ thị đối xứng qua gốc toạ độ
O
.
- Hàm số nghịch biến trên các khoảng
( ; )( )k k k
.
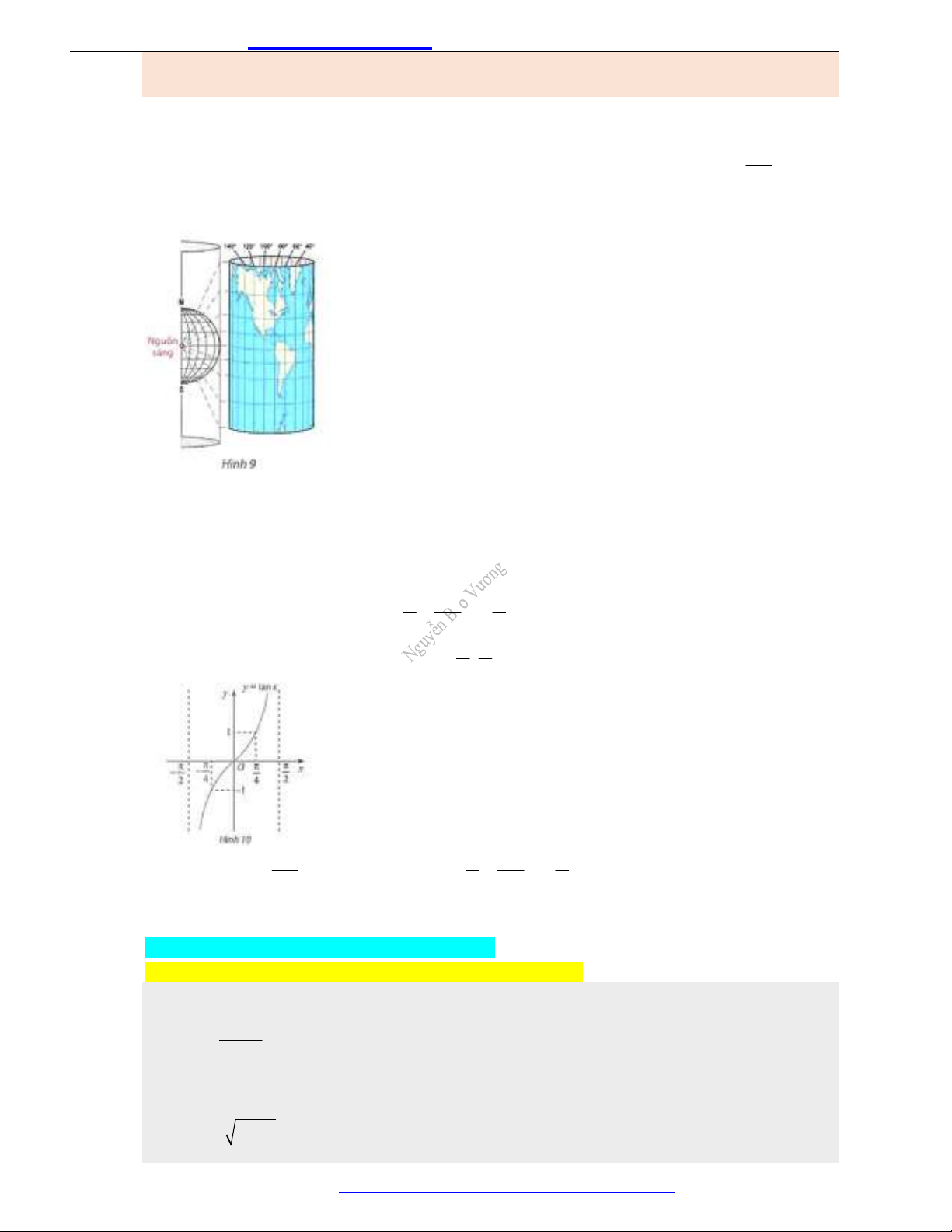
Ví dụ 4. Trong Địa lí, phép chiếu hình trụ được sử dụng để vẽ một bản đồ phẳng như trong Hình
9. Trên bản đồ phẳng lấy đường xích đạo làm trục hoành và kinh tuyến
0
làm trục tung. Khi đó
tung độ của một điểm có vĩ độ
( 90 90)
được cho bởi hàm số
20 tan ( )
180
y cm
.
Sử dụng đồ thị hàm số tang, hãy cho biết những điểm ở vĩ độ nào nằm cách xích đạo không quá
20 cm
trên bản đồ.
(Theo https://geologyscience.com/geology/types-of-maps/)
Giải
Vì điểm nằm cách xích đạo không quá
20 cm
trên bàn đồ nên ta có
20 20y
.
Khi đó
20 20 tan 20
180
hay
1 tan 1
180
.
Ta có
90 90
khi và chi khi
2 180 2
.
Xét đồ thị hàm số tany x trên khoảng
;
2 2
(Hình 10
)
.
Ta thấy
1 tan 1
180
khi và chi khi
4 180 4
hay
45 45
.
Vậy trên bản đồ, các điểm cách xích đạo không quá
20 cm
nằm ở vĩ độ từ
45
đến
45
.
PHẦN B. BÀI TẬP TỰ LUẬN (PHÂN DẠNG)
DẠNG 1. TẬP XÁC ĐỊNH CỦA HÀM SỐ LƯỢNG GIÁC
A. Với hàm số
f x
cho bởi biểu thức đại số thì ta có:
1.
1
2
f x
f x f x
, điều kiện: *
1
f x
có nghĩa
*
2
f x
có nghĩa và
2
0f x
.
2.
21
,
m
f x f x m
, điều kiện:
1
f x
có nghĩa và
1
0f x
.
Điện thoại: 0946798489 TOÁN 11-CHÂN TRỜI SÁNG TẠO
Trang 5
3.
1
22
,
m
f x
f x m
f x
, điều kiện:
1 2
,
f x f x
có nghĩa và
2
0
f x
.
B. Hàm số
sin ; cosy x y x
xác định trên
, như vậy
sin ; cos
y u x y u x
xác định khi và chỉ khi
u x
xác định.
*
tan
y u x
có nghĩa khi và chỉ khi
u x
xác định và
;
2
u x k k
.
*
cot
y u x
có nghĩa khi và chỉ khi
u x
xác định và
;u x k k
.
Chú ý
Ở phần này chúng ta chỉ cần nhớ kĩ điều kiện xác định của các hàm số cơ bản như sau:
1. Hàm số
siny x
và
cosy x
xác định trên
.
2. Hàm số
tany x
xác định trên
\2k k
.
3. Hàm số
coty x
xác định trên
\k k
.
C. Dạng chứa tham số trong bài toán liên quan đến tập xác định của hàm sô lượng giác.
Với
f
S D
(là tập xác định của hàm số
f x
) thì
, max
S
f x m x S f x m
.
, min
S
f x m x S f x m
.
0 0
, min
S
x S f x m f x m
0 0
, max
S
x S f x m f x m
.
Câu 1. (SGK-CTST 11-Tập 1) Tìm tập xác định của các hàm số sau:
a)
1
cos
y
x
;
b)
tan
4
y x
;
c)
2
1
2 sin
y
x
.
Câu 2. Tìm tập xác định của các hàm số sau
a)
tan 2
6
y x
b)
cot 2
3
y x
c)
2
sin 2
y
x
d)
2
2cos 3 2
y x x
Câu 3. Tìm tập xác định các hàm số sau:
a)
2
1 2
1 cos 2
x
y
x
b)
2
3
cos
1
x
y
x
c)
2 2siny x
d)
sin 1y x
e)
1 cos
1 cos
x
y
x
. f)
tan
4
y x
g)
2
cot 2
4 1 cos
y x
x
.
Câu 4. Tìm tập xác định của các hàm số sau: