17/04/2017
1
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
PHÉP TÍNH TÍCH PHÂN
HÀM MỘT BIẾN
CHƯƠNG 4
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Định nghĩa nguyên hàm
•Định nghĩa: Cho hàm f(x) liên tục trên (a,b). Ta nói F(x)
là một nguyên hàm của f(x) trên (a,b) nếu:
•Ví dụ:
, ,F x f x x a b
laø moät nguyeân haøm cuûa
treân
laø moät nguyeân haøm cuûa a treân R.
2
tan 1 tan
\ 2 1 2
ln
x x
x x
R n
a a
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Tích phân bất định
•Tích phân bất định của hàm f(x) ký hiệu:
•Được xác định như sau:
•F(x) là một nguyên hàm của f(x).
•C: hằng số tùy ý.
f x dx
f x dx F x C
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Tính chất
)
) .
)
i f x dx f x
ii k f x dx k f x dx
iii f x g x dx f x dx g x dx
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Công thức nguyên hàm cơ bản
1. 2.
3. 4.
5. 6.
x x
k dx x dx
dx dx
x
x
a dx e dx
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Các phương pháp tính
•Phân tích, biến đổi
•Đổi biến dạng 1
•Đổi biến dạng 2
•Tích phân từng phần
17/04/2017
2
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Phương pháp phân tích
•Chia đa thức
•Nhân liên hợp
•Áp dụng các công thức biến đổi hàm số
•Sử dụng công thức cơ bản
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Ví dụ
•Tính các tích phân sau
2 1
2
2
2
0
1
2 1
. . 3
1
3 1
. .
. lim 1
x x
x
x
x
a dx b e e dx
x x
x x
c dx d x x dx
x
dt
et t
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Đổi biến số dạng 1
•Đặt t=u(x)
•Ta đưa tích phân về dạng:
•Phải tìm u’ hoặc biến đổi u’ xuất hiện trước.
•Thường đặt u bằng căn thức, mũ của e, mẫu số
hay biểu thức trong ngoặc
. u'
f u x x dx f t dt
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Ví dụ
•Tính các tích phân sau
3 4
2 5
. 1 .
c x x dx
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Đổi biến số dạng 2 (tham khảo)
•Đặt: x=u(t)
•Biến đổi biểu thức tính tích phân về dạng:
.
f x dx f u t u t dt
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Ví dụ
•Tính các tích phân sau
2 1
2
2
0 0
1 2
22
0
2
) 4 ) 1
) )
1
1
x
a x dx b dx
x
dx dx
c d
x
x x
17/04/2017
3
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Tích phân từng phần
•Đưa biểu thức tính tích phân về dạng:
•Đặt:
•Khi đó:
.
f x dx h x g x dx
'du h x
u h x
dv g x dx
v g x dx
. .f x dx h x g x dx uv v du
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Tích phân từng phần
•Đưa biểu thức về dạng tích
•Chọn hàm để đặt u và dv
•Chú ý: chọn sao cho việc tính đạo hàm và tích
phân dễ tính.
•Áp dụng công thức:
.udv uv v du
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Các dạng cần nhớ
. sin
. cos
. .
n
n
ax
n
P x ax dx
P x ax dx
P x e dx
. ln .
. arctan .
. arcsin .
n
n
n
P x x dx
P x x dx
P x x dx
Luong giac nguoc garit
thuc
Lo
Da Luong M
giac
u
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Ví dụ
•Tính các tích phân sau
2
1 0
1
2
0
3
) ln ) 2 1 sin
) cos ) arctan
e
a x xdx b x xdx
c x xdx d x xdx
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Công thức Tanzalin
•Tính tích phân sau:
6
2 . 3 2
x x dx
6 7 8
2 1
2 . 3 2 3 2 3 2
21 252
x
x x dx x x C
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Công thức Tanzalin
•Tính tích phân sau:
. sin .x x dx
. sin . . cosx sinx
x x dx x C
Đạo hàm Tích phân Dấu Tích
x sinx
1 -cosx + -xcosx
0 -sinx - sinx
17/04/2017
4
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Công thức Tanzalin
•Tính tích phân bất định:
•Đáp số:
2
1.x x dx
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Tích phân hàm mũ
•Công thức:
•Ví dụ. Tính các tích phân sau:
1
x x
ax b ax b
u u
i e dx e C
ii e dx e C
a
iii e du e C
4
0
2
4 3
0
) 3 ) 4
) ) D a .
x x
I
x Tx
a A e dx b B e x dx
c C xe dx d e dx
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Ví dụ
•Tìm phương trình đường cong y=y(x) biết nó đi
qua điểm (1;0) và:
•Đáp án:
3
x
dy e
dx
3 2
2
x
y e e
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Diện tích dưới đường cong
•Ví dụ. Một tòa nhà có cổng dạng parabol. Ta cần
gắn kính cho cổng nhà. Hỏi diện tích kính cần
gắn là bao nhiêu?
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Diện tích dưới đường cong
•Ta chia hình cần tính thành nhiều hình chữ nhật nhỏ.
•Cộng hết diện tích các hình chữ nhật nhỏ lại
•Ta được diện tích tương đối của hình cần tính
•Độ cao của mỗi hình chữ nhật
được xác định thông qua giá trị
của hàm số.
Ví dụ. Tại điểm c thì hình chữ
nhật có độ cao là f(c)
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
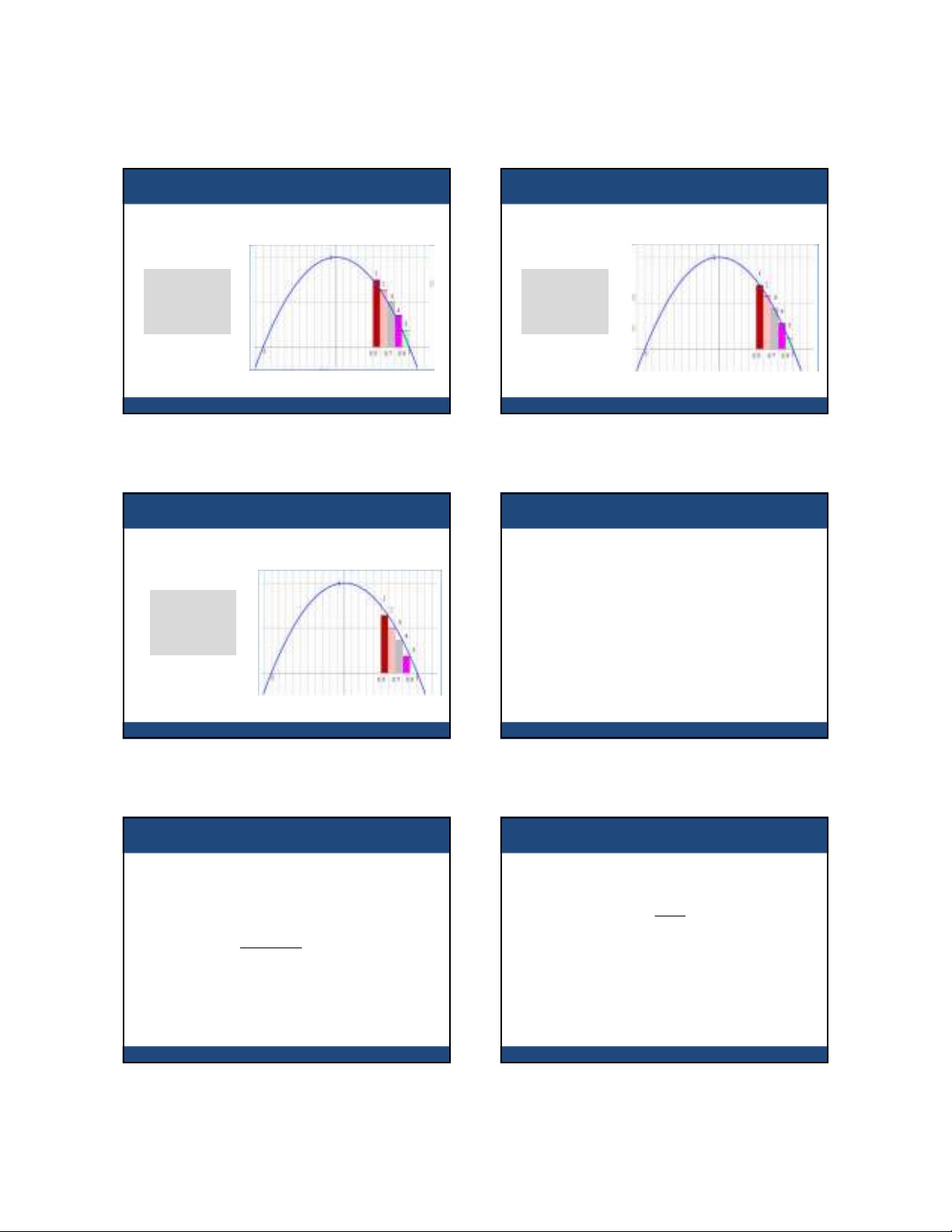
Diện tích dưới đường cong
•Tìm diện tích dưới đường cong y=1-x
2
giữa x-
0,5 và x=1
•Sử dụng công thức tổng các diện tích hình chữ
nhật để tính xấp xỉ (giả sử n=5)
17/04/2017
5
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Diện tích dưới đường cong
•Với n=5 ta có chiều rộng mỗi hcn là: 0,1
•Ta tính tổng của 5 hcn sau:
5
1
0, 75.0,1 0, 64.0,1 0, 51.0,1 0.36.0,1 0,19.0, 1 0, 245
i
i
A S
Cách 1. Xấp xỉ
bằng tổng các
hình chữ nhật
ngoài
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Diện tích dưới đường cong
•Với n=5 ta có chiều rộng mỗi hcn là: 0,1
•Ta tính tổng của 5 hcn sau:
5
1
0, 64.0,1 0, 51.0,1 0, 36.0,1 0, 19.0,1 0 0, 1 0,17
i
i
A S
Cách 2. Xấp xỉ
bằng tổng các
hình chữ nhật
trong
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Diện tích dưới đường cong
•Để có được giá trị xấp xỉ tốt hơn ta lấy giá trị
trung bình của 2 cách tính trên
•Ta được:
0, 245 0,17 0, 2075
2
A
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Diện tích dưới đường cong
•Với n=5 ta có chiều rộng mỗi hcn là: 0,1
•Ta tính tổng của 5 hcn sau:
5
1
0, 6975 0, 5775 0, 4375 0, 2775 0, 0975 .0,1 0,20875
i
i
A S
Cách 3. Xấp xỉ
bằng tổng các
hình chữ nhật
ở giữa
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Nhận xét
•Nếu ta chia thành 10 hình chữ nhật với n=10 thì kết quả
tìm được xấp xỉ tốt hơn
•Tính theo cách 1 ta có kết quả sau:
•Theo cách 2 ta có:
•Theo cách 3 ta có: Trung bình cộng cách 1,2:
10
1
0, 75 0, 6975 ..... 0,19 0, 0975 .0, 05 0, 226875
i
i
A S
10
1
0, 6975 ..... 0,19 0, 0975 0 .0, 05 0,189375
i
i
A S
10
1
0,208438
i
i
A S
10
1
0,208125
i
i
A S
Bài giảng Toán Cao cấp 1 Nguyễn Văn Tiến
Tích phân xác định
•Định nghĩa: Nếu f là hàm số xác định trên [a;b].
3. Goïi laø caùc ñieåm maãu baát kyø
trong nhöõng ñoaïn con
* * *
1 2
*
1
, ,...,
; .
n
i i i
x x x
x x x
2. Giaû söû laø caùc ñieåm bieân
nhöõng ñoaïn con Ta coù
012
, , , ...,
. : .
n
i
a x x x x b
x a i x
1. Chia ñoaïn thaønh phaàn baèng nhau,
coù chieàu roäng
[ , ]a b n
b a
x
n