
Bài tập cơ học
lượt xem 1.183
download
 Download
Vui lòng tải xuống để xem tài liệu đầy đủ
Download
Vui lòng tải xuống để xem tài liệu đầy đủ
Mời các bạn cùng tham khảo Bài tập cơ ứng dụng để ôn tập kiến thức và rèn luyện kỹ năng giải bài tập. Hi vọng với tài liệu này sẽ giúp các bạn đạt điểm cao trong kỳ thi sắp tới. Chúc các bạn thi tốt!
Bình luận(0) Đăng nhập để gửi bình luận!
Nội dung Text: Bài tập cơ học
- Bμi tËp tù gi¶i m«n c¬ häc øng dông PhÇn I. C¬ häc vËt r¾n tuyÖt ®èi C Bμi 1.1 Cho c¬ cÊu bèn kh©u b¶n lÒ víi c¸c chiÒu dμi (2) 1 1 1 AB = BC = CD = AD = a; ω1 = 100s −1 . (3) 3 3 4 ω1 B 1. XÐt ®iÒu kiÖn quay toμn vßng cña kh©u (1) vμ (3). (1) ϕ 2. X¸c ®Þnh ω2 vμ ω3 khi ϕ1 = 00, 1800 vμ khi kh©u (1) 1 D (4) vμ (2) duçi th¼ng. H×nh 1.1 Bμi 1.2 Cho c¬ cÊu bèn kh©u b¶n lÒ ph¼ng víi c¸c chiÒu 1 dμi AB = BC = CD = AD = a; ω1 = 60s −1 . 2 (2) C 1. XÐt ®iÒu kiÖn quay toμn vßng cña kh©u (1) vμ (3). B ω1 (3) I 2. X¸c ®Þnh ω3 khi ϕ1 = 00, 600. (1) r ϕ1 3. Khi kh©u (1) vμ (2) duçi th¼ng h·y x¸c ®Þnh v I (I lμ D A (4) trung ®iÓm kh©u 2). H×nh1. 2 Bμi 1.3 Cho c¬ cÊu bèn kh©u b¶n lÒ ph¼ng nh− h×nh 1.3, 1 1 víi c¸c chiÒu dμi AB = BC = CD = DA = a ; C (2) 3 3 I n1 = 120vg / ph . B 1. X¸c ®Þnh ω2 vμ ω3 khi ϕ1 = 90 . 0 M (3) ω1 ω (1) ϕ1 2. X¸c ®Þnh tû sè i13 = 1 khi ϕ1 = 1800. ω3 (4) D r r A 3. X¸c ®Þnh v I vμ v M khi ϕ1 = 900 (I lμ trung ®iÓm H×nh 1.3 cña BC, M lμ trung ®iÓm cña CD). Bμi 1.4 Cho c¬ cÊu tay quay con tr−ît nh− h×nh 1.4. Cho biÕt AB = a; BC = 2a; ⎧0 e=⎨ ; ω = 100s-1. B ⎩a 2 ω1 (2) 1. Kh©u (1) cã quay ®−îc toμn vßng (1) ϕ1 I hay kh«ng? A (4) C e 2. X¸c ®Þnh hμnh tr×nh cña kh©u (3). M v 3. X¸c ®Þnh i31 = 3 khi gãc ϕ1 = (3) ω1 H×nh 1.4 9 0 0. r r 4. X¸c ®Þnh v3 khi ϕ1 = 2700 vμ v I khi ϕ1 = 00 (I lμ trung ®iÓm cña BC) 1
- Bμi 1.5 Cho c¬ cÊu culÝt nh− h×nh 1.5. BiÕt AB =a; AC = a 3 , B CM = a; ω = 90 s-1. (2) (1) ω1 1. X¸c ®Þnh gãc l¾c ψ cña kh©u (3) vμ qu·ng ®−êng M ®i ®−îc khi AB quay ®−îc 2 vßng. (3) A 2. X¸c ®Þnh ω3 khi ϕ1 = 00, 900. ϕ1 r M 3. X¸c ®Þnh v M khi ϕ1 = 1800. Bμi 1.6 Cho c¬ cÊu cam cÇn ®Èy ®¸y b»ng nh− h×nh 1.6. Cam lμ (4) mét ®Üa trßn (C1, R) quay lÖch t©m víi t©m sai e = R = O1C1, H×nh 1.5 C kho¶ng c¸ch t©m O1O2 = 4R. 1. X¸c ®Þnh gãc l¾c ϕ2 cña cÇn l¾c ®¸y b»ng (2). 2. X¸c ®Þnh ω2 khi ϕ1 = 00, 1800. v2 K 1 2 K 2 1 A ω1 ω2 C1 R M ω1 C1 ϕ1 ϕ2 ϕ1 O2 O1 O1 x 3 3 H×nh 1.6 H×nh 1.7 Bμi 1.7 Cho c¬ cÊu cam nh− h×nh 1.7. Cam lμ mét 2 r ®Üa trßn (C1, R) quay lÖch t©m víi t©m sai e =R = O1C1. 3 ω1 (1) C1 r 1. H·y gäi tªn c¬ cÊu cam ®· cho vμ x¸c ®Þnh v A (A n»m O1 ϕ1 (2) trªn kh©u (2)) theo ω1 vμ ϕ1. (3) M 2. X¸c ®Þnh qu·ng ®−êng cña ®iÓm A khi cam quay ®−îc 2 vßng. Bμi 1.8 Cho c¬ cÊu cam cÇn l¾c. Cam lμ thanh O1C1 g¾n chÆt O2 vμo ®Üa trßn (C1, r). CÇn (2) lμ mét thanh cã r·nh réng 2r ®Ó ®Üa trßn tr−ît trong ®ã. BiÕt O1C1 = O1O2 = 6R; O2M = 3R; H×nh 1.8 1. X¸c ®Þnh qu·ng ®−êng M (thuéc cÇn) ®i ®−îc khi 4r y cam quay ®−îc 1 vßng. 2. X¸c ®Þnh vËn tèc cña ®iÓm M khi ϕ1 = 90 . 0 v2 Bμi 1.9 Cho c¬ cÊu cam nh− h×nh 1.9. Cam lμ mét thanh 2 th¼ng quay quanh O, cÇn ®Èy lμ mét ®Üa trßn (C2, r). 1 C2 r 1. X¸c ®Þnh qu·ng ®−êng cÇn ®i ®−îc khi cam rêi vÞ ω1 trÝ ϕ1 = 00 ®Õn ϕ1 = 300. K r ϕ1 O1 2. X¸c ®Þnh v 2 cña cÇn ë hai vÞ trÝ trªn. x 3 H×nh 1.9 2
- Bài 1.10 Cho cơ cấu tay quay con trượt ở trạng thái cân bằng dưới tác dụng của các lực và ngẫu lực, như trên hình 1.10. Xác định phản lực liên kết ở các khớp động A, B, C và mômen của ngẫu lực phát động M1. Bỏ qua ma sát ở các khớp động. PhÇn II. C¬ häc vËt r¾n biÕn d¹ng H×nh 1.10 Bài 2.1 Vẽ biểu đồ M=2kNm m=10kNm/m 60kN M lực dọc của thanh A chịu lực như hình 2.1. 40kN B d 2m C A Bài 2.2 Vẽ biểu đồ 100cm mômen xoắn của 50cm q=15kN/m B 2m thanh chịu lực như F=40cm2 H×nh 2.2 C hình 2.2. P=qa q 2m M*=qa2 Bài 2.3 Vẽ biểu đồ 60kN 0 lực cắt và mômen 2 1 3 uốn của dầm chịu lực D a a a như hình 2.3. H×nh 2.1 H×nh 2.3 Bài 2.4 Cho một hệ treo liên kết và chịu lực như hình 2.4. Hãy xác định lực cho phép [q] tác dụng lên hệ F1=1cm2 theo hai điều kiện sau: l1=2m 1) Điều kiện bền của thanh 1 và 2 với [σ] F2=2cm2 = 16kN/cm2. l2=1m q 2) Theo điều kiện cứng: chuyển vị thẳng B đứng của điểm A: ΔA ≤ 1,5 cm. Biết các thanh AB, DE là tuyệt đối cứng, A 2m 3m cho E = 2.104 kN/cm2. H×nh 2.4 Bài 2.5 Cho một trục chịu xoắn như hình 2.5. 1 Hãy vẽ biểu đồ mômen xoắn Mz và ứng M∗ M∗ 2M∗ suất tiếp lớn nhất τmax dọc theo trục z. D B 2 Xác định giá trị của M* để trục làm việc d C 2d A z an toàn về bền và cứng, biết [τ] = 10kN/cm2; [θ] = 2o; d = 6 cm; G = a a a 8.103 kN/cm2; a = 50 cm. Hình 2.5 3 Tính góc xoắn của mặt cắt D so với mặt cắt A. Bμi 2.6 Cho mét dÇm cã liªn kÕt vμ chÞu lùc nh− h×nh 2.6. Thanh g·y khóc CIK tuyÖt ®èi cøng. BiÕt E, a, h, b, [σ]. 1. VÏ biÓu ®å lùc c¾t vμ m«men uèn. 3
- 2. X¸c ®Þnh t¶i träng cho phÐp [q], bá b/2 qua ¶nh h−ëng cña lùc c¾t. 3. TÝnh ®é vâng vμ gãc xoay t¹i C. h h/2 a/2 P=qa Bμi 2.7 Cho mét dÇm cã mÆt c¾t ngang, liªn kÕt vμ chÞu lùc nh− h×nh 2.7. q I b K kN a a BiÕt a (cm); q ( ); b = ;h= . C m 40 40 D A B 1. VÏ biÓu ®å lùc c¾t Qy vμ m«men a a a uèn Mx. 2. TÝnh gi¸ trÞ øng suÊt ph¸p lín nhÊt H×nh 2.6 trong dÇm: max⏐σz⏐ (N/cm2). 3. TÝnh ®é vâng t¹i C vμ t¹i D, biÕt E. q P=ql P1=9qa M=2qa2 P2=qa q d A A C h B D B C 2a 2a 2a l/2 l/2 l/2 b H×nh 2.8 H×nh 2.7 Bμi 2.8 Cho mét dÇm cã liªn kÕt vμ chÞu lùc nh− h×nh 2.8. 1. VÏ biÓu ®å lùc c¾t Qy vμ m«men uèn Mx. 2. X¸c ®Þnh d, biÕt l , q vμ [σ]. Bá qua ¶nh h−ëng cña lùc c¾t. 3. TÝnh ®é vâng vμ gãc xoay t¹i C do P g©y ra, biÕt EJx =const. Bμi 2.9 Cho mét dÇm liªn kÕt vμ chÞu lùc nh− h×nh 2.9. BiÕt P1 = 5qa; M1 = 5qa2; M2 = 2qa2. P 1 M1 M2 q 1. VÏ biÓu ®å lùc c¾t Qy vμ m«men uèn Mx. 2. TÝnh gi¸ trÞ øng suÊt ph¸p lín nhÊt A trong dÇm: max⏐σz⏐, biÕt Wx = B C D 3 -4 8a .10 . a a 2a 3. TÝnh ®é vâng t¹i C vμ gãc xoay t¹i D. Cho biÕt EJx. Hình 2.9 Bμi 2.10 Trôc cã hai b¸nh r¨ng, b¸n kÝnh r1=6 cm; r2=12 cm. Lùc theo ph−¬ng tiÕp tuyÕn cña chóng t−¬ng øng lμ P1, P2. Gãc gi÷a c¸c lùc nμy víi ph−¬ng th¼ng ®øng y lμ n 2 α1=45 , α2=30 . ChiÒu 1 0 0 P1x P2x dμi cña ®o¹n trôc z a=10cm; b=15cm; l=25 cm. Trôc cã sè α1 α2 vßng quay n=1000 P1y P2 P1 a b l vg/ph; c«ng suÊt P2y truyÒn t¶i cña trôc Hình 2.10 N=600 kW. X¸c ®Þnh ®−êng kÝnh trôc theo thuyÕt bÒn ¦STLN. BiÕt [σ]=12 kN/cm2. 4
- HƯỚNG DẪN GIẢI Bài 1.10: Cho cơ cấu tay quay con trượt ở trạng thái cân bằng dưới tác dụng của các lực và ngẫu lực, như trên hình 5-7. Xác định phản lực liên kết ở các khớp động A, B, C và mômen của ngẫu lực phát động M1. Bỏ qua ma sát ở các khớp động. Hình 5-7 Bài giải ⇒ Cơ cấu tay quay con trượt có một bậc tự do. ⇒ Để xác định phản lực liên kết ta phải tách ra từ cơ r ấu nhóm tĩnh định (2, c 3) không chứa khâu phát động (1). Phản lực liên kết R12 tại B (từ khâu 1 tác rτ rn dụng lên khâu 2) được phân thành hai thành phần: R12 và R12 , phản lực liên r kết R 43 tại C (từ khâu 4 tác dụng lên khâu 3). ⇒ Từ điều kiện cân bằng nhóm tĩnh định: r M M C = 0 ⇒ R12 BC − M 2 = 0 ⇒ R12 = 2 = P n n BC rn ⇒ Chiều của R12 như chiều giả thiết trên hình 5-7b. r rr rτ rn R = 0 ⇒ R + R 43 + R12 + R12 = 0 5
- r rτ ⇒ Có thể tìm các ẩn R 43 và R12 bằng cách lập phương trình hình chiếu trên r r phương P và R 43 hoặc dựng đa giác lực. Ở đây ta giải theo cách dựng đa giác lực (hình 5-7c). Từ đó ta có: P24 τ R 43 = R12 = P 3 (R ) + (R ) n2 τ2 R12 = = 2P 12 12 r ⇒ Phản lực liên kết R12 làm với phương r AC góc 600. Sau khi xác định được R12 , dễ dàng tìm được lực liên kết tại khớp quay C: r R 32 (từ khâu 3 tác dụng lên khâu 2) đối r xong với R12 (theo điều kiện cân bằng của r r khâu 2) còn R 23 =- R 32 . ⇒ Xét ngẫu lực M1 và phản lực liên kết trên khâu phát động 1. Phản lựcr liên kết của r khâu 2 đối với khâu 1: R 21 = - R12 . ⇒ Từ điều kiện cân bằng của khâu 1, ta có: r rr M1 = M A (R 21 ) ⇒ M1 = R 21r cos300 = Pr 3 r r ⇒ Phản lực liên kết của giá 4 đối với khâu 1: R 41 = − R 21 ⇒ R 41 = P ⇒ Chú ý: Có thể xác định mômen M1 theo nguyên lý di chuyển khả dĩ như sau - Tưởng tượng cho khâu 1 di chuyển khả dĩ δϕ1 , vì cơ cấu có 1 bậc tự do nên các di chuyển khả dĩ δϕ2 của khâu 2 (quay quanh tâm vận tốc tức thời P24) và δs3 của con trượt 3, xác định phụ thuộc δϕ1 . Theo nguyên lý di chuyển khả dĩ: rr rr rr M1δϕ1 + M 2 δϕ2 + Pδ s3 = 0 hay M1δϕ1 − M 2 δϕ2 − Pδs3 = 0 δs δϕ2 M1 = M 2 +P 3 Từ đó ta có: δϕ1 δϕ1 δs3 v3 δϕ2 ω2 AB = = = = AP13 Chú ý rằng: ; δϕ1 ω1 P24 B δϕ1 ω1 ⎛ ⎞ ω2 v AB M1 = M 2 + P 3 = P⎜ r 3 + AP13 ⎟ = Pr 3 Ta được: ω1 ω1 P24 B ⎝ ⎠ 6
- 7

CÓ THỂ BẠN MUỐN DOWNLOAD
-

Giải bài tập: Cơ nhiệt Vật lý đại cương - Lương Duyên Bình
 79 p |
79 p |  8346
|
8346
|  2049
2049
-

Bài tập Cơ lý thuyết
 16 p |
16 p |  4249
|
4249
|  904
904
-

Bài tập Cơ học kèm lời giải
 79 p |
79 p |  980
|
980
|  325
325
-

Bài tập Cơ Học Lưu Chất - 2
 9 p |
9 p |  1033
|
1033
|  310
310
-
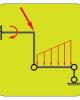
Bài tập Cơ lý thuyết: Động lực học
 2 p |
2 p |  1240
|
1240
|  304
304
-

Bài tập Cơ học lượng tử - Hoàng Đỗ Ngọc Trầm
 15 p |
15 p |  826
|
826
|  264
264
-

Bài tập cơ lưu chất - Trường ĐH Bách khoa HCM
 27 p |
27 p |  1398
|
1398
|  102
102
-

Bài giảng Cơ học chất lưu: Bài tập
 3 p |
3 p |  684
|
684
|  102
102
-

Bài tập cơ học đại cương - Phần 1 Cơ học vật rắn - Chương ôn tập
 10 p |
10 p |  318
|
318
|  82
82
-

Bài tập cơ học đại cương - Phần 1 Cơ học vật rắn - Chương 3
 10 p |
10 p |  266
|
266
|  77
77
-

Bài tập Hóa học thực tiễn phần Vô cơ
 162 p |
162 p |  472
|
472
|  72
72
-

Bài tập cơ học đại cương - Phần 1 Cơ học vật rắn - Chương 1
 11 p |
11 p |  283
|
283
|  69
69
-

Bài tập cơ học đại cương - Phần 1 Cơ học vật rắn - Chương 2
 19 p |
19 p |  328
|
328
|  67
67
-

Bài tập cơ học đại cương - Phần 2 Dao động và sóng cơ - Chương 1
 15 p |
15 p |  229
|
229
|  59
59
-

Bài tập Hóa học hữu cơ (Tập 1)
 73 p |
73 p |  448
|
448
|  27
27
-

Bài tập Sinh học tế bào
 5 p |
5 p |  186
|
186
|  17
17
-

Đề thi kết thúc học phần học kì 1 môn Bài tập Sinh học năm 2019-2020 có đáp án - Trường ĐH Đồng Tháp
 2 p |
2 p |  14
|
14
|  3
3
Chịu trách nhiệm nội dung:
Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA
LIÊN HỆ
Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM
Hotline: 093 303 0098
Email: support@tailieu.vn








