MỘT SỐ BÀI TẬP CƠ HỌC LÝ THUYẾT
Câu 1. Chất điểm khối lượng
m
chuyển động với vận tốc đầu
0
v
từ điểm
A
theo
phương vuông góc với
0
OA r
=
uuur ur
(
O
là gốc tọa độ) dưới tác dụng của lực
F Cmr
ur r
(
C
là hằng số dương). Tìm phương trình quỹ đạo và vận tốc của vật.
+) Ta có
[ ] [ ] 0 .
dL
M r mv r F L const
dt
= = Ù + Ù = Þ =
ur
uur r r r ur r ur uuuuur
Do vậy quỹ đạo chuyển động nằm trong một mặt phẳng.
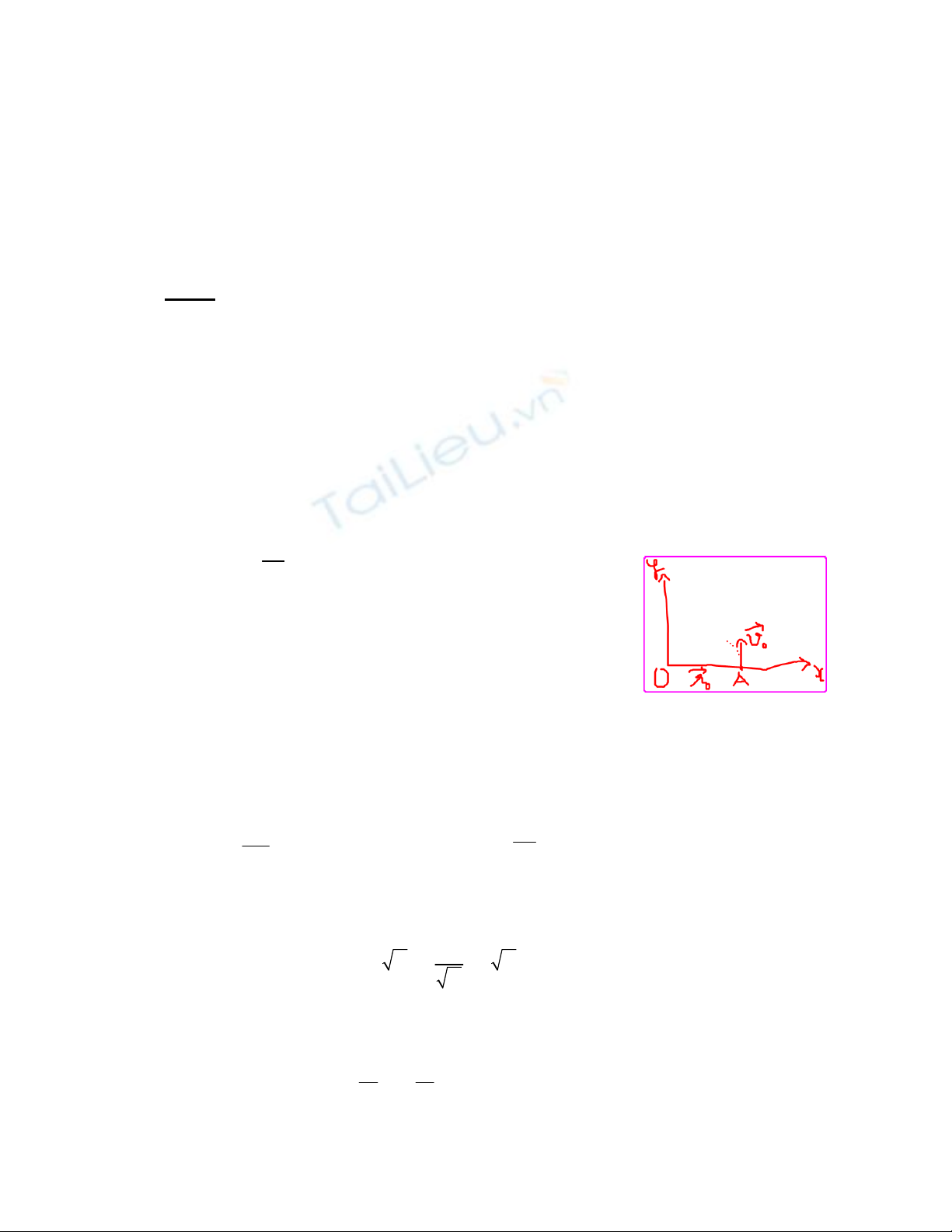
+) Chọn hệ tọa độ Oxy như hình vẽ.
+) PTCĐ 2
2
,
d r
C r
dt
= -
r
r
trong đó
( )
0 0
00
, .
tt
dr
r r v
dt
==
æ ö
÷
ç÷
= =
ç÷
ç÷
ç
è ø
r
r
r r
+) Giải ra ta được 0
0
cos sin .
v
r r C t C t
C
= +
r
r r
+) Phương trình quỹ đạo 2 2
2 2
0 0
1.
x y
C
r v
+ =
+) Vận tốc của vật
2 2 2 2
0 0 0 0
sin cos sin cos .
v C r C t v C t v Cr C t v C t
= - + Þ = +
r rr
Câu 2. Đĩa tròn nằm ngang có khối lượng
M
phân bố đều, bán kính của đĩa là
.
R
Đĩa
có thể quay không ma sát quanh trục thẳng đứng đi qua tâm. Trên mép đĩa có một chất
điểm khối lượng
.
m
Ban đầu đĩa và chất điểm quay với vận tốc góc
0
.
w
Tính vận tốc
của hệ khi chất điểm dịch chuyển về vị trí cách tâm đĩa một khoảng
.
r
+) Do các ngoại lực tác dụng lên hệ có phương song song với trục quay nên tổng
mômen ngoại lực tác dụng lên hệ theo trục quay Oz bằng 0, tức là
0.
z
M
=
+) Ta có
0.
zz
dL M
dt
= =
Suy ra
.
z
L const
=
+) Chọn chiều dương là chiều quay của đĩa lúc đầu.
+) Mômen xung lượng của hệ theo phương trục Oz được bảo toàn nên ta có
2
2 2 2 2
0 0 0
2 2
1 1 ( 2 )
.
2 2 2
M m R
MR mR MR mr MR mr
+
w + w = w+ w Þ w = w
+
Câu 3. Phà và một ôtô đạu trên phà có vận tốc
0
.
v
Sau đó ô tô chuyển động trên phà
với vận tốc tương đối
u
hướng từ đầu phà đến cuối phà. Biết khối lượng của phà là
M
và khối lượng của ô tô là
.
m
Tính vận tốc của phà khi ô tô đang chuyển động.
+) Chọn chiều dương là chiều chuyển động của phà lúc đầu. Xét hệ gồm phà và ôtô.
+) Do tổng ngoại lực tác dụng lên hệ theo phương ngang bằng không nên
0 .
l
xx x
dP
F P const
dt
= = Þ =
+) Động lượng của hệ theo phương ngang được bảo toàn nên ta có
0 0
( ) ( ) .
m
M m v Mv m v u v v u
M m
+ = + - Þ = + +
(với
v
là vận tốc của phà khi ôtô đang chuyển động).
Câu 1. Một viên đạn khối lượng
m
được bắn đi trong trọng trường đều với vận tốc
0
v
ur
hợp với phương ngang góc
.
a
Lực cản
.
F mgkv
= -
ur r
Tìm PTCĐ và vận tốc của vật.
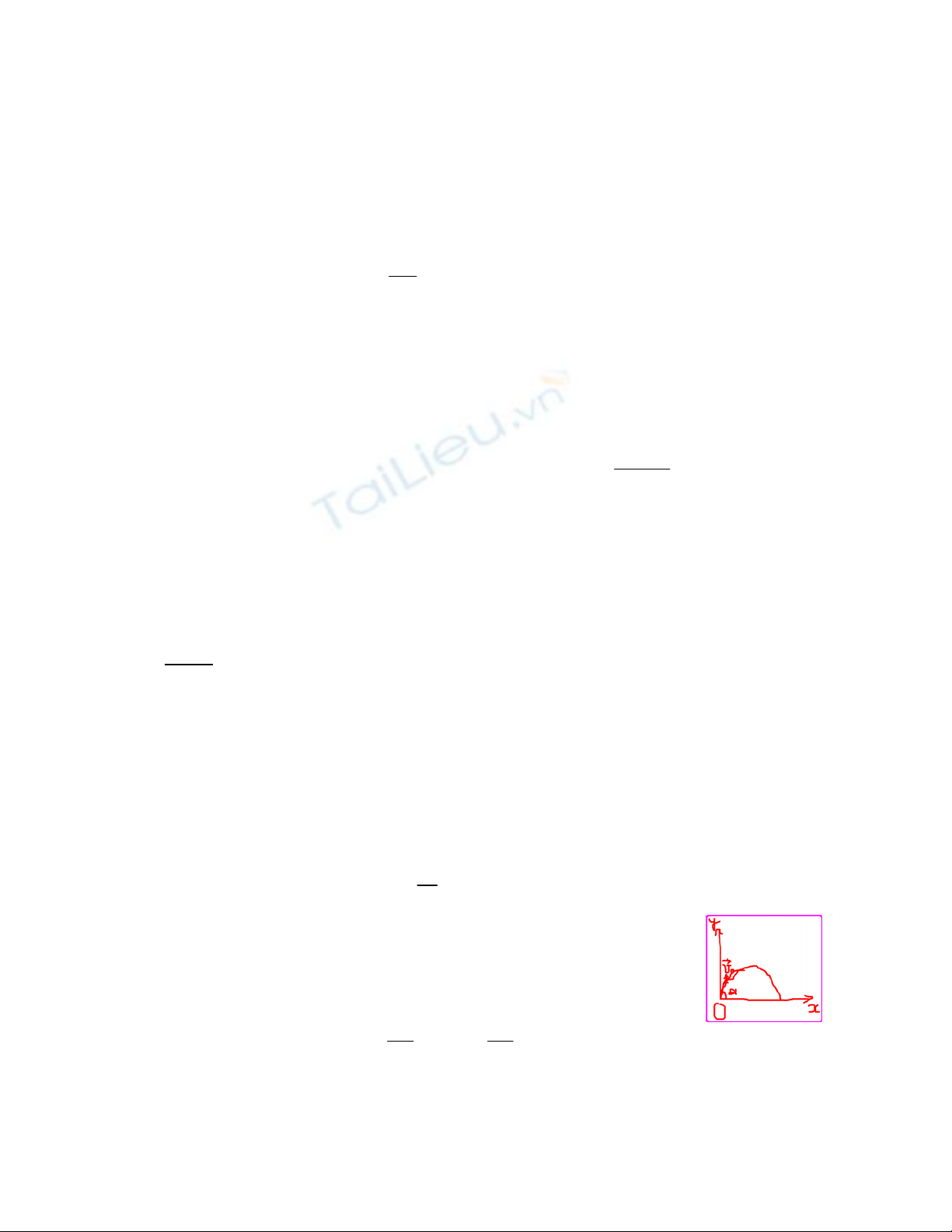
+) Dễ thấy quỹ đạo cđ của đạn nằm trong một mặt phẳng. Chọn hệ trục Oxy như h.vẽ.
+) PT cđộng
,
dv
g gkv
dt
= -
r
r
r trong đó
0 0
(0) cos , (0) sin , (0) (0) 0.
x y
v v v v x y
= a = a = =
+) Chiếu lên Ox, Oy ta được
, .
y
x
x y
dv
dv
gkv g gkv
dt dt
= - = -
+) Giải ra ta được
( )
0
0
0
cos 0
0 0
sin 0
cos
1
sin sin 1
1
x
y
vt
xkgt
x
x
v
vt
kgt
yy
vy
dv gk dt v v e
v
dv v v v e
gk dt k
v
k
-
a
-
a
ì
ï
ï
ï= -
ïì
ï ï = a
ï ï
ï ï
ï ï æ ö
Þ
í í ÷
ç
ï ï ÷
= a + - a -
ç
ï ï ÷
ç÷
= ç
ï ï è ø
ï ï
î
ï
ï-
ï
ï
î
ò ò
ò ò
( )
( )
( )
0
0
0 0
0
0 0
0 0
cos
cos 1
1 1 1
1
sin 1 .
sin sin 1
x t kgt kgt
yt
kgt
kgt
v
dx v e dt x e
kg
y t v e
dy v v e dt k kg k
k
--
-
-
ì
ïì
ï
ïa
ï
ï= a = -
ï
ïï
ïï
ïÞ
í í æ ö
ï ïé ù
æ ö ÷
ç
ï ï
÷
ç ÷
= - - a -
ê ú ç
ï ï
÷
= a + - a - ÷
çç
ï ÷ ï ÷
ç
ê ú
çè ø
÷
ç
ï ï
è ø î
ê ú
ïë û
î
ò ò
ò ò
Câu 2. Các vật
1 2
,
m m
nối nhau bằng dây không dãn vắt qua ròng rọc,
chúng trượt trên nêm vuông góc
.
m
Tính độ dịch chuyển của nêm khi
1
m
hạ xuống một đoạn
.
s
+) Chọn chiều dương như hình vẽ. Xét hệ gồm các vật
1
,
m m
và
2
.
m
+) Do tổng ngoại lực tác dụng lên hệ theo phương ngang bằng không nên
( )
0
l
c
d Mv F
dt
= =
(với
1 2
M m m m
= + + ).
Suy ra
0
c c
v const v
= Þ =
(do ban đầu hệ đứng yên). Suy ra
.
c
x const
=
+) Độ biến thiên khối tâm của hệ bằng không, do đó
1 2
1 2
cot
( cot ) ( ) 0 m m
m x m x s m x s x s
M
a +
D + D + a + D + = Þ D = -
(với
x
D
là độ dịch chuyển của nêm).
+) Vậy nêm sẽ chuyển động ngược lại một đoạn 1 2
cot
.
m m
s s
M
a +
D =
Câu 3. Phà và một ôtô đạu trên phà có vận tốc
0
.
v
Sau đó ô tô chuyển động trên phà
với vận tốc tương đối
u
hướng từ đầu phà đến cuối phà. Biết khối lượng của phà là
M
và khối lượng của ô tô là
.
m
Tính vận tốc của phà khi ôtô đang chuyển động.
+) Chọn chiều dương là chiều chuyển động của phà lúc đầu. Xét hệ gồm phà và ôtô.
+) Do tổng ngoại lực tác dụng lên hệ theo phương ngang bằng không nên
0 .
l
xx x
dP
F P const
dt
= = Þ =
+) Động lượng của hệ theo phương ngang được bảo toàn nên ta có
0 0
( ) ( ) m
M m v Mv m v u v v u
M m
+ = + - Þ = + +
(với
v
là vận tốc của phà khi ôtô đang chuyển động).
Câu 1. Một cano khối lượng
m
bắt đầu chuyển động thẳng trên mặt nước dưới tác
dụng của lực kéo không đổi
F
ur
song song mặt nước và lực ma sát trượt có hệ số
.
kv
m= Tìm phương trình chuyển động và vận tốc giới hạn của cano.
+) Dễ thấy quỹ đạo cđ của cano nằm trên 1 đường thẳng. Chọn trục Ox như hình vẽ.
+) Phương trình chuyển động
,
ms
F F P N
dv
dt m
+ + +
=
ur ur
r r
r
trong đó 0 0
( ) 0,( ) 0.
t t
v x
= =
= =
r r
r
r