!" #$ % !
&
−
'
− ($ ) * + )! ,-
. $#!
) !
/ 0 +
1 2 3 ! (
−
−
−
− / 0 +−
4 5 ,% ! $ ! #
−
−−
+! / +! +! + 0
6 ($ ,- 7 '
−
0 / +
8
($ ) * + )! ,-
/ + 0
9 5 ,% !
||
−
−
−
|| /|| ||−+||−
: )! ; ) )! ' ≤≤ ! % !( ,%
! )!
/ +
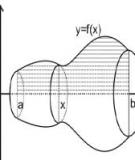
< 2 3 ! (
−
−
−
/
0 +
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
= $ !#
−
5 +!
/ 0 +
&>
−
−
5 +!
−
/
+ 0
&& ($ ,% ! $ !# ! $?
−
+! / +! +! −+ +!
&1 5 ,% ! $ !# @7 '
/ +
&4 5 ,% ! $ !#
7 /)!
0 /−
+
&6 5 ,% ! A. !$ )B ||
−
|| /|| || −+||
&8 $ !#
)3 7 /)!
7 ' . , ' % 5 +!
/+−
&9 5
−
7 /)! ; . $ !# ' )3
/
+
&: ,% !
@ C
−
− −
−
−
' C
−
− −−
−
D ,% ,* ,E
/− + 0
&< )! 3 !( A/) B ' ) #$
D ,% ,E
0 /∀ +
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
&= ($ ,- +! '
−
−
/ −+−
1> ($ / # 7 /)!
−
−
# 4 / 0 # 6 + # 8
1&
−
($ ,-
0 / − +
11
−
5 +!
0 / +−
14
−
'
−
−
5 +!
/− 0 +−
16 ∈
7 /)! +! − 5 +!
−
− /
−
−
+−
18
−
7
−
5 +!A
− / +−
19 5 ,% !
||
−
−−
'
−
|| / 0 || − +||
1: 5 ,% ! $ ! #
−
− −
−
−
0 /+−
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
1< $ !#
'
−
5 +!
−
/−
−
+ 0
1= ($ / # 7 /)!
−
−
−
0 / # 4 # 6 + # 8
4> $ !#
−
'
− 5 ,% ! $ !#
− / 0 +
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
!" #$ # %#& !'( !) & * +
+ { }
− −
−
!
, { } "# $% & &'
&
{ } { }
{ } ! ( { } ) *
- { } ) * $% & &' &
&" "# ' + &" "# ' +
* , ! - # ' + { }
. .
{ }
, *
∀ ∃ !
/ , ) / { }&" "# ' + $% &
&' &
."# { }&" "# ' + !{ −} 0 ,
0 . { } ) $% &
&' & ' " 12../ 3.../ .(.. &" "# / # " - # ' +
* , { }12..
{} .(.. { }!{ }3...
1 .
{ }
, *
∀ !
2 { } $% & &' &
{ } ( { −} ) 0
{ }# " ' + !{ }
3 { } "# / { }&" "# ' +
$% & &' &
( { −} )
4
56 ! - # ' + { }
+4 − ∈
∀! ∃
++ { }789(
! $ ,
+, : - # ' + $; & &
&" "# ' +
* &, !{ } "#
+-
:
" &" "# '
+ & "
$% & &' &
- # ' +
&
,
!
Simpo PDF Merge and Split Unregistered Version - http://www.simpopdf.com
![Quyển ghi Xác suất và Thống kê [chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20251030/anh26012006/135x160/68811762164229.jpg)
