
Tiết 24 : LIÊN HỆ GIỮA DÂY
VÀ KHOẢNG CÁCH
TỪ TÂM ĐẾN DÂY
I – Mục tiêu:
HS nắm được các định lý về liên hệ giữa dây và khoảng cách từ tâm đến
dây của 1 đường tròn.
HS biết vận dụng các định lý trên để so sánh độ dài 2 dây, so sánh
khoảng cách từ tâm đến dây.
Rèn luyện tính chính xác trong chứng minh và suy luận.
II- Chuẩn bị: GV: thước, com pa.
HS: thước, compa
III- Tiến trình bài dạy:
1) Ổn định :Lớp 9A2:…………Lớp 9A3:………….. Lớp 9A4……………..
2) Kiểm tra: (5’)
? Nhắc lại quan hệ vuông góc giữa đường kính và dây trong đường tròn ?
3) Bài mới:

Hoạt động của GV Hoạt động của HS Ghi bảng
Hoạt động 1: Bài toán (8’)
GV đặt vấn đề như khung chữ sgk
GV yêu cầu hs vẽ hình vào vở, và
nghiên cứu bài giải sgk/104.
? Bài toán cho biết gì ? yêu cầu tìm gì ?
? Để c/m được đẳng thức trên vận dụng
kiến thức nào?
? Kết luận của bài toán có đúng trong
trường hợp 1 dây hoặc 2 dây là đường
kính của đường tròn không ?
GV giới thiệu chú ý sgk
HS đọc bài toán
HS vẽ hình vào vở
HS tự đọc sgk.
HS trả lời
HS vận dụng định lý
Pitago.
HS trả lời .
HS đọc chú ý
* Bài toán: sgk/104
(0;R)
dây AB, CD
0H AB
0K CD
0 D
C
A B
K
H
0H2+ HB2 = 0K2 + KD2
CM
Sgk / 104
* Chú ý: sgk/104
Hoạt động 2: Liện hệ giữa dây và khoảng cách từ tâm đến dây (20’)
GV cho hs làm ?1
? Bài toán cho biết gì ? tìm gì ?
? Từ kết quả 0H2 + HB2 = 0K2 + KD2.
hãy c/m ?1
GV yêu cầu 2 HS trình bày c/m
HS đọc ?1
HS trả lời
HS nêu hướng c/m:
HS trình bày c/m trên
?1
a) 0H AB; 0K CD (đ/l đường
kính dây)
AH = BH =
2
1AB

GV bổ xung sửa sai
? Qua bài toán này ta có thể rút ra kết
luận gì ?
GV giới thiệu định lý 1.
GV nhấn mạnh định lý và lưu ý: hs AB,
CD là 2 dây trong cùng 1 đường tròn,
0H, 0K là khoảng cách từ tâm 0 đến dây
AB và CD.
GV cho hs làm ?2
? Bài toán yêu cầu làm gì ?
GV yêu cầu hs thảo luận.
bảng
HS khác nhận xét
HS trả lời
1-2 hs đọc định lý
HS đọc ?2
HS trả lời
HS hoạt động nhóm
trình bày
Đại diện nhóm trả lời
và CK = KD =
2
1CD;
nếu AB = CD
HB = KD HB2 = KD2
mà 0H2+ HB2 = 0K2 + KD2 (cm t)
0H2 = 0K2 0H = 0K
b) Nếu 0H = 0K 0H2 = 0K2
mà 0H2+ HB2 = 0K2 + KD2 (cm t)
HB2 = KD2 HB = KD hay
2
1AB =
2
1CD AB = CD
* Định lý 1: sgk/ 104
?2
a) Nếu AB > CD thì
2
1AB >
2
1CD
HB > KD HB2 > KD2
mà 0H2+ HB2 = 0K2 + KD2 (cm t)
0H2 < 0K2 mà 0H; 0K > 0 nên
0H < 0K
GV bổ xung nhận xét trên bảng nhóm.
? Từ bài toán trên hãy phát biểu thành
định lý ?
GV giới thiệu định lý 2
GV cho hs làm ?3
? Bài toán cho biết gì ? tìm gì ?
GV yêu cầu hs vẽ hình ghi gt kl
? Để so sánh độ dài BC với AC ta đi so
sánh 2 độ dài nào ?
? 0 là giao 3 đường trung trực trong tam
giác suy ra 0 có đặc điểm gì ?
? Vậy ta suy ra điều gì ?
GV yêu cầu hs trình bày c/m
GV tương tự hãy c/m phần b
HS phát biểu
1-2 hs đọc định lý
HS đọc ?3
HS trả lời
HS thực hiện
HS: so sánh 0E và 0F
HS: 0 là tâm đ/tr
ngoại tiếp tam giác.
HS AC = CB
HS trình bày c/m
b) Chứng minh tương tự 0K > 0H
ta cũng AB > CD
* Định lý 2:sgk/105
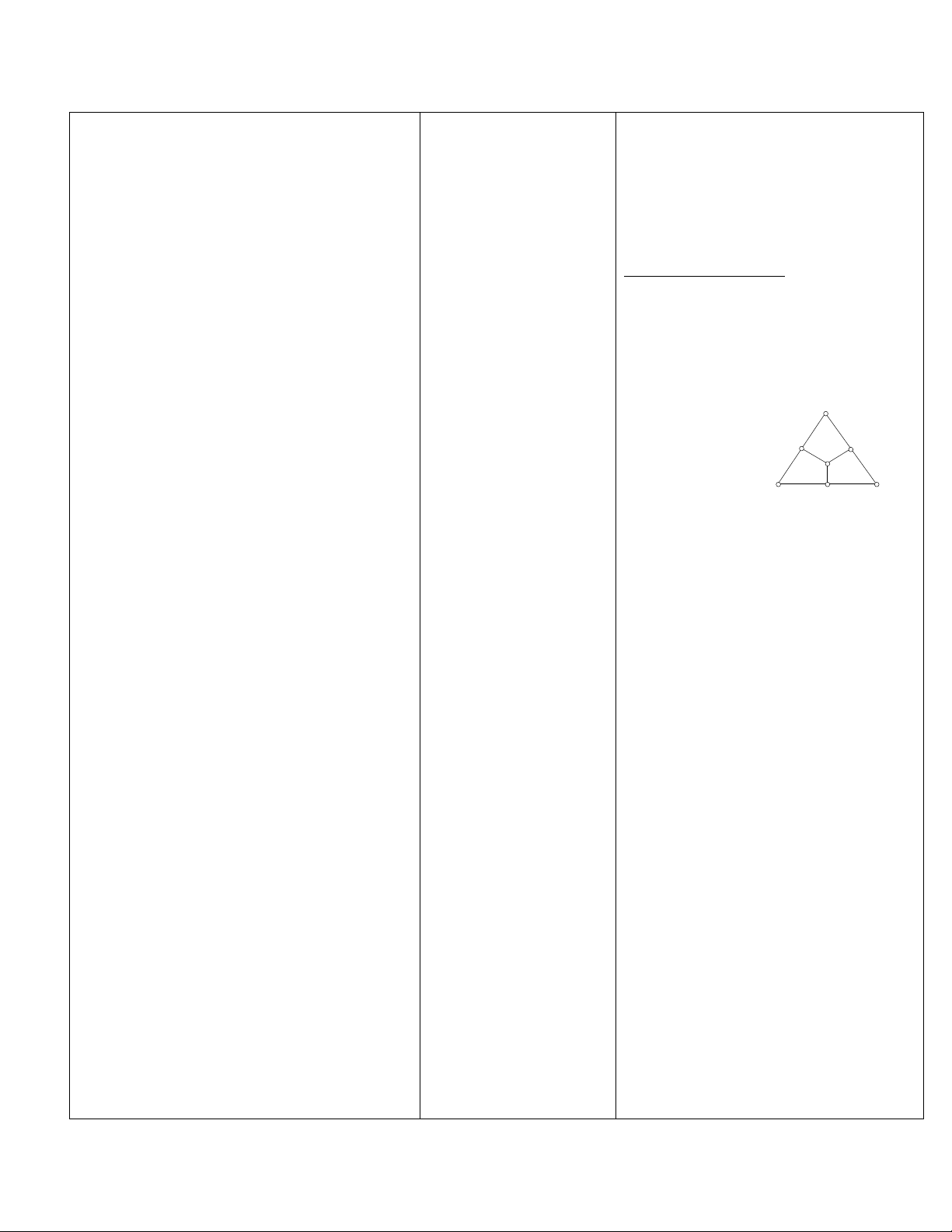
?3
ABC;
0 giao 3
đường tr/ trực
D AB;
DA = DB
A
BC
0
E
F
D
F AC; FA = FC
E BC; BE = EC
So sánh a. BC và AC
b. AB và AC
C/M
a) 0 là giao 3 đường tr/ trực trong
ABC 0 là tâm đ/ tròn ngoại
tiếp ABC; mà 0E = 0F (gt)
AB = BC (đ/l 1). Có 0D > 0E
và 0E = 0F(gt) 0D > 0F

AB < AC ( đ/l 2)
b) HS tự so sánh
Hoạt động 4: Củng cố - luyện tập (10’)
GVyêu cầu hs nêu cách vẽ hình.
Giới thiệu hình đã vẽ sẵn trên bảng phụ.
? Yêu cầu HS ghi gt kl ?
? Muốn tính xem 0H = ? Ta làm như thế
nào ?
? Tính HB =? áp dụng kiến thức nào?
GV yêu cầu hs trình bày
? C/m CD = AB ta c/m như thế nào ?
GV hướng dẫn hs c/m tứ giác 0HIK là
hình chữ nhật.
HS đọc đề bài
HS ghi gt kl
HS tính 0B, BH
HS định lý Pitago
1 HStrình bày
HS khác trình bày
vào vở
HS kẻ 0K CD
C/m 0K = 0H
Bài tập 12 (sgk /106)
(0;5) AB = 8
I AB AI = 1
I CD;
CDAB
a. 0H =?
b. CD = AB
0
D
CA
B
H
K
C/M
a.Kẻ 0H AB . Ta có
AH = HB =
2
1AB = 4 (cm)
0HB vuông có
0B2 = BH2 + H02 đ/lPitago)
52 = 42 = 0H2 0H = 3
b. HS tự c/m


























