intTypePromotion=1
zunia.vn Tuyển sinh 2024 dành cho Gen-Z zunia.vn zunia.vn
ADSENSE
 » 
 » 

Tài liệu ôn tập chương Toán lớp 10 (Sách Kết nối tri thức với cuộc sống) - Chương 3: Hệ thức lượng trong tam giác

Chia sẻ: _ _ | Ngày: | Loại File: PDF | Số trang:39

Thêm vào BST
Báo xấu
1
lượt xem 0
download
 
  Download Vui lòng tải xuống để xem tài liệu đầy đủ

Tài liệu này cung cấp tóm tắt lý thuyết về các hệ thức lượng trong tam giác vuông và tam giác thường, ôn tập các công thức tính cơ bản, kèm theo bài tập trắc nghiệm và tự luận, hướng dẫn lời giải chi tiết. Tài liệu này giúp học sinh áp dụng các hệ thức lượng để giải bài tập và các vấn đề thực tế. Mời các bạn cùng tham khảo "Tài liệu ôn tập chương Toán lớp 10 (Sách Kết nối tri thức với cuộc sống) - Chương 3: Hệ thức lượng trong tam giác" để làm chủ lượng giác.

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Tài liệu ôn tập chương Toán lớp 10 (Sách Kết nối tri thức với cuộc sống) - Chương 3: Hệ thức lượng trong tam giác

  1. TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Điện thoại: 0946798489 ÔN TẬP CHƯƠNG 3. HỆ THỨC LƯỢNG TRONG TAM GIÁC • TOÁN 10 • |FanPage: Nguyễn Bảo Vương PHẦN 1. LÝ THUYẾT – VÍ DỤ Bài 5. Giá trị lượng giác của một góc từ 0 đến 180 A - Kiến thức cần nhớ 1. Điểm M  x0 ; y0  nầm trên nửa đường tròn đơn vị sao cho    XOM Khi đó: sin   y0 , cos   x0 , sin  tan   cos     90 . cos  cot   sin      0 ,   180 . 1 tan   cot       0 ;90 ;180 . 2. Khi   0 thì sin   0, cos   1 . Khi   90 thì sin   1, cos   0 . Khi 0    90 thì 0  sin   1, 0  cos   1 , tan   0 và cot   0 . Khi 90    180 thì 0  sin   1, 1  cos   0 , tan   0 và cot   0 . 3. Bảng giá trị lượng giác (GTLG) của một số góc đạc biệt cần nhớ GTLG 0 30 45 60 90 120 135 150 180 sin 0 1 1 3 1 3 1 1 0 2 2 2 2 2 2 cos 1 3 1 1 0 1 1 3 1    2 2 2 2 2 2 tan 0 1 1 3 ‖  3 1 1 0  3 3 cot ‖ 3 1 1 0 1 1  3 ‖  3 3 Bảng 3.1. Giá trị lượng giác của một số góc đặc biệt 4. Tính chất a) Giá trị lượng giác của hai góc phụ nhau: Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
  2. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/    sin 90    cos  , cos 90    sin   tan  90     cot  , cot  90       tan  . b) Giá trị lượng giác của hai góc bù nhau:    sin 180    sin  , cos 180     cos  tan 180       tan  , cot 180      cot  .  c) Hệ thức cơ bản (bài tập 3.3, SGK Toán 10, tập một): sin 2   cos2   1 1 1  tan 2   cos2    90   1 1  cot 2   2 sin   0    180 .   tan   cot   1 0    180 ,  90 .  B - Ví dụ Ví dụ 1. Không dùng máy tinh, tính giá trị của các biều thức sau: a) A  sin 45  cos135  cos 60  sin150  cos 30  sin120 ; b) B  tan135  cot 60  cot 30  tan 60  tan150 c) C  2sin 60  tan150  cos180  cot 45 . Giải 1 1 3 a) Từ Bảng 3.1 ta thấy sin 45    cos135 , cos 60   sin150 và cos 30   sin120. 2 2 2 1  1  1 1 3 3 1 1 3 Từ đó suy ra A      2  2  2  2   2  4  4  1. 2  2 1 1 b) Do tan135  1, cot 60  , cot 30  tan 60  3, tan150   nên 3 3 1  1  B  1   3  3     1. 3  3 3 1 c) Cũng từ Bảng 3.1,sin 60  , tan150   , cos180  1 và cot 45  1 . Suy ra 2 3 3  1  C  2     (1)  1  0. 2  3 Chú ý. Nếu đề ý đến mối liên hệ giữa các góc có trong biểu thức, như các góc bù nhau, các góc phụ nhau, thì ta có thể giải bài toán theo cách sau: a) Do 135  180  45 ,150  180  30 ,120  180  60 nên   A  sin 45   cos 45  cos 60  sin 30  cos30  sin 60 1  1  1 1 3 3 1 1 3             1. 2  2 2 2 2 2 2 4 4 b) Do 135  180  45 , 60  90  30 ,150  180  30 nên  B  1  1  tan 60   tan 30  1.  c) Do 150  180  30 nên 3  1    C  2sin 60   tan 30  cos180  cot 45  2    2    (1) 1  0. 3 Trang 2 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  3. Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG 1 Ví dụ 2. Cho góc  , 0    180 thoả mãn cos    . 3 a) Tính tan  . b) Tính giá trị của biểu thức P  tan   2 cot  . Giải 1 1 a) Do cos     0 nên  là góc tù và tan     1  2 2 . 3 cos 2  1 b) Do tan   cot   1 và tan   2 2 nên cot    và bởi vậy 2 2  1  5 P  2 2  2      2 2 2 1 Nhận xét. Khi tính tan  từ cos  nhờ đẳng thức 1  tan 2   sai lầm thường gặp của học sinh là cos 2  1 mặc định coi tan    1 mà quên mất tan   0 khi  là góc tù. cos 2  Bài 6. Hệ thức lượng trong tam giác A - Kiến thức cần nhớ Quy ước, kí hiệu. Với tam giác ABC , ta thường sử dụng các kí hiệu sau: a, b, c : Độ dài các cạnh BC , CA, AB ha , hb , hc : Độ dài đường cao kẻ từ A, B, C abc p : Nửa chu vi của tam giác 2 S : Diện tích của tam giác R, r : Bán kinh đường tròn ngoại tiếp, bán kính đường tròn nội tiếp ma , mb , mc : Độ dài đươong trung tuyến kẻ từ A, B, C . Định lí côsin. Trong tam giác ABC , ta có a 2  b 2  c 2  2bc cos A . a b c Định lí sin. Trong tam giác ABC , ta có    2R . sin A sin B sin C Các công thức tính diện tích: 1 1 abc S  aha  ab sin C   pr  p( p  a)( p  b)( p  c). 2 2 4R B - Ví dụ Ví dụ 1. Cho tam giác ABC có a  8, b  9, c  6 . a) Tính số đo các góc của tam giác. b) Tính diện tích, bán kinh đường tròn ngoại tiếp, bán kính đường tròn nội tiếp. độ dài các đường cao của tam giác. Giải a) Áp dụng định lí côsin, ta có b 2  c 2  a 2 81  36  64 53 cos A    . 2 bc 296 108 ˆ Suy ra A  603639 . ˆ ˆ Hoàn toàn tương tự, tính được B  78355 , C  40 4816 .  8  9  6 23 7 5 b) Do a  8, b  9, c  6 nên tam giác ABC có nửa chu vi p   . Suy ra p  a  , p  b  và 2 2 2 2 11 23 7 5 11 8855 p  c  . Từ đó, theo công thức Heron ta được diện tích của tam giác là S      . 2 2 2 2 2 4 Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
  4. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ S 8855 abc 432 Suy ra bán kinh đường tròn nội tiếp r   và bán kinh đường tròn ngoại tiếp R   . p 46 4S 8855 Nhận xét - Định lí côsin giúp ta giải tam giác trong trường hợp biết ba cạnh của tam giác hoặc biết hai cạnh và góc xen giữa hai cạnh đó (bài tập 3.8 và 3.9 ). 53 8855 - Từ cos A  , sử dụng hệ thức cơ bản (bài tập 3.3, SGK Toán 10, tập một), tính được sin A  . 108 108 1 8855 Từ đó, sử dụng công thức S  bc sin A ta cũng thu được S  . 2 4 ˆ ˆ Ví dụ 2. Cho tam giác ABC có A  15 , c  6 và B  120 . a) Tính độ dài các cạnh a, b . b) Tính độ dài bán kính đường tròn ngoại tiếp tam giác và diện tích của tam giác. c) Tính độ dài đường cao ha . Giải ˆ ˆ ˆ ˆ ˆ a) Do A  15 , B  120 nên C  180  A  B  45 . Áp dụng đinh lí sin ta được: c 6 a sin C .sin A  sin 45   .sin15  3 3  1 c 6 b .sin B  .sin120  3 6 sin C sin 45 b) Theo định lí sin, bán kính đường tròn ngoại tiếp của tam giác là c 6 R   3 2. 2 sin C 2 sin 45 Do a  3( 3  1), b  3 6, c  6 và R  3 2 nên abc 3( 3  1)  3 6  6 9 3( 3  1) S   . 4R 43 2 2 2S 9 3( 3  1) c) Từ kết quả của phần b), suy ra ha   3 3. a 3( 3  1) Nhận xét - Định lí sin giúp ta giải tam giác trong trường hợp biết hai góc và một cạnh của tam giác. 1 - Ở phần b) cũng có thể sử dụng công thức S  ab sin C để tính diện tích của tam giác. 2 Ví dụ 3. Cho tam giác ABC . Chứng minh rằng: 2 b2  c 2 a 2 a) ma   ; 2 4 1 1 1 1 b)    . ha hb hc r Giải a) Gọi M là trung điểm của BC . Khi đó ma  AM . Có hai trường hợp sau xảy ra: Trường hợp 1. b  c . Trong trường hợp này AM cũng chính là đường cao kẻ từ A của tam giác. Do đó a2 b2  b2 a2 ma  AC 2  CM 2  b 2  2   . 4 2 4 Trường hợp 2. b  c . Không mất tính tổng quát, xét trường hợp b  c , trường hợp còn lại chứng minh tương tự. Trang 4 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  5. Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Gọi D là chân đường cao kẻ từ A . Do b  c nên D thuộc tia MC . Áp dụng định lí Pythagore cho tam giác ADB , ta có AB 2  BD 2  AD 2  ( BM  MD )2  AD 2  BM 2  2  BM  MD  MD 2  AD 2 Suy ra AB 2  BM 2  2  BM  MD  AM 2 1 Một cách tương tự, áp dụng định lî Pythagore cho tam giác ADC , cũng được AC 2  AD 2  ( MC  MD )2  MC 2  2  MC  MD  AM 2  2  Từ (1) và (2) suy ra     AB 2  AC 2  BM 2  CM 2  2( BM  MD  CM  MD )  2 AM 2  BM 2  CM 2  2 AM 2 2 b2  c 2 a 2 hay ma   . 2 4 b) Từ công thức tinh diện tich tam giác suy ra 1 p a b c 1 1 1        . r S 2S 2S 2S ha hb hc Nhận xét 2 b2  c2 a2 - Công thức ma   cho phép ta tính được độ dài đường trung tuyến của một tam giác, khi biết ba 2 4 cạnh của nó. Có thể thu được công thức này bằng cách làm như trong bài 3.16 (Toán 10, tập một). - Nếu gọi E là điểm đối xứng với A qua M , thì tứ giác ABEC là một hình bình hành với hai đường chéo BC , AE . Khi đó công thức tính độ dài đường trung tuyến ở phần a) trở thành BC 2  AE 2  AB 2  BE 2  EC 2  CA2 . Ví dụ 4. Cho tam giác ABC có các góc thoả mãn sin C  2  sin B  cos A . Chứng minh rằng tam giác ABC là một tam giác cân. Giải Áp dụng các định lí sin và côsin, ta có b2  c2  a2 sin C  2 sin B cos A  c  2 b cos A  c  2 b   c 2  b 2  c 2  a 2  a  b. 2 bc Vậy tam giác ABC cân tại C . Ví dụ 5. Để đo chiều cao của một tòa nhà, người ta chọn hai điểm A và B thẳng hàng với chân C của tòa nhà, cách nhau 15 m . Sử dụng giác kế, từ A và B tương ứng nhìn thấy đỉnh D của tòa nhà dưới các góc 35 và 40 so với phương nằm ngang. Hỏi chiều cao của tòa nhà đo được là bao nhiêu mét? Giải   Do CBD  40 , BAD  35 nên   40  35  5 . Áp dụng định lí sin cho tam giác ABD ta được ADB AB 15 BD   sin A    sin 35 . sin D sin 5 Từ đó suy ra chiều cao của tòa nhà bằng  15 h  CD  BD  sin CBD    sin 35  sin 40   63, 45(  ). m sin 5 Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
  6. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ PHẦN 2. BÀI TẬP TỰ LUẬN Đề Câu 1. Tính giá trị biểu thức P  sin 30 cos 60  sin 60 cos30. Câu 2. Rút gọn P  cos 20  cos 40  .....  cos160  cos180 Câu 3. Tính giá trị biểu thức P  sin 2 10  sin 2 20  sin 2 30  ...  sin 2 80. Câu 4. Cho biểu thức      1  3  1  P  x    tan   x  .tan   x   cos   x .  sin 2  2  x   2 cos 2 x  2  cos2  x     2  sin   x         2  Rút gọn biểu thức P  x  ta được P  x   m.sin 2 x  n.cos 2 x . Tính S  m 2  n 2 ? Câu 5. Một chiếc đu quay có bán kính 75 m , tâm của vòng quay ở độ cao 90 m (tham khảo hình vẽ). Thời gian quay hết 1 vòng của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét? Câu 6. ˆ Tam giác ABC có AB  5, BC  7, CA  8 . Khi đó số đo góc A bằng bao nhiêu? Câu 7. Cho tam giác ABC có B  30 , C  55 và cạnh AC  16cm . Tính cạnh AB ? Câu 8. Cho tam giác ABC có B  40 , C  55 và cạnh AC  20cm . Tính cạnh BC ? Câu 9. Cho tam giác ABC có B  30 và cạnh AC  16cm . Tính bán kính đường tròn ngoại tiếp tam giác ABC? Câu 10. Cho tam giác ABC có B  50 và cạnh AC  20cm . Tính bán kính đường tròn ngoại tiếp tam giác ABC? Trang 6 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  7. Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Câu 11. Cho tam giác ABC có B  35 , C  50 và cạnh AC  12cm . Tính cạnh AB ? Câu 12. Cho ABC có bán kính đường tròn nội tiếp là r  4 , nửa chu vi p  10 . Diện tích tam giác ABC bằng bao nhiêu? Câu 13. Cho tam giác ABC có a  6, b  6, c  8 . Khi đó diện tích của tam giác bằng bao nhiêu? Câu 14. Cho tam giác ABC có   60, AB  6, AC  8 . Tính BC . A Câu 15. Tam giác ABC có AB  4, BC  6, AC  2 7 . Điểm M thuộc đoạn BC sao cho MC  2 MB . Tính độ dài AM . Câu 16. Cho tam giác ABC biết a  2 3, b  2 2, c  6  2 . Số đo của góc lớn nhất của tam giác bằng bao nhiêu?   Câu 17. Tam giác ABC có B  300 , C  450 , AB  3 . Tính cạnh AC   Câu 18. Tam giác ABC có tổng hai góc B và C bằng 150 0 và BC  a . Tính bán kính đường tròn ngoại tiếp tam giác ABC Câu 19. Cho tam giác ABC thoả mãn hệ thức b  c  2a . Chứng minh rằng sin B  sin C  2 sin A.  Câu 20. Cho tam giác ABC biết AB  4 , AC  5 , BAC  60 . Khi đó diện tích của tam giác ABC bằng bao nhiêu? Câu 21. Cho tam giác ABC biết a  7 , b  8 , c  9 . Khi đó diện tích của tam giác ABC bằng bao nhiêu?   Câu 22. Cho tam giác ABC biết a  6 , B  85 , C  65 . Khi đó bán kính đường tròn ngoại tiếp ABC bằng bao nhiêu? Câu 23. Cho hình chữ nhật ABCD có cạnh AB  4 , BC  6 , M là trung điểm của BC , N là điểm trên cạnh CD sao cho ND  3NC . Khi đó diện tich tam giác AMN bằng bao nhiêu? Câu 24. Cho tam giác ABC có A  120o ; b  8; c  5. Tính bán kính đường tròn nội tiếp tam giác ABC . Câu 25. Cho tam giác ABC có A  60o ; b  12; c  13. Tính đường cao lớn nhất của tam giác ABC .   Câu 26. Cho tam giác ABC , có A  105 , C  45 và AC  10 . Tính độ dài cạnh AB . Câu 27. Cho tam giác ABC có BC  8 , CA  7 , AB  5 . Trên cạnh BC lấy điểm M sao cho BM  5 . Tính bán kính r của đường tròn nội tiếp tam giác ACM . Câu 28. Cho tam giác ABC có AB  2 , AC  3 , BC  4 . Gọi M là trung điểm cạnh AB . Tính bán kính R của đường tròn ngoại tiếp tam giác BCM . Câu 29. Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí     A đến vị trí C và tiến hành đo BAC , BCA . Biết AC  25 m, BAC  5957 ', BCA  829 ' . Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)? Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 7
  8. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ Câu 30. Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là   35 ; khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1, 5 m . Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là   75 ; khoảng cách từ mặt đất đến mắt bạn B cũng là 1, 5 m . Biết chiều cao của tòa nhà là h  20 m (Hình vẽ). Chiếc diều bay cao bao nhiêu mét so mặt đất (làm tròn kết quả đến hàng đơn vị)?    Câu 31. Cho M là điểm nằm trong tam giác ABC sao cho MAB  MBC  MCA   . S  SABC . Chứng minh rằng cot   cot A  cot B  cot C  Câu 32. Tam giác nhọn ABC có AC  b, BC  a , BB ' là đường cao kẻ từ B và CBB '   . Tìm công thức tính bán kính đường tròn ngoại tiếp R của tam giác ABC được tính theo a, b và  ? Câu 33. Cho tam giác ABC có độ dài đường trung tuyến ma , mb , , mc thỏa mãn 5ma  mb  mc2 . Khi đó tam 2 2 giác ABC là tam giác gì? sin B  sin C Câu 34. Cho tam giác ABC thỏa mãn: sin A  . Khi đó tam giác ABC là tam giác gì? cos B  cos C Câu 35. Ông X cần đo diện tích mảnh đất hình tứ giác, ông đi theo chu vi mảnh đất, lần lượt đo độ dài các cạnh và một góc như hình vẽ.Tính diện tích của mảnh đất đó(làm tròn đến m 2 ). Lời giải tham khảo Câu 1. Tính giá trị biểu thức P  sin 30 cos 60  sin 60 cos30. Trang 8 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  9. Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Lời giải sin 30  cos 60 Vì 30 và 60 là hai góc phụ nhau nên  sin 60  cos 30 Nên P  sin 30 cos 60  sin 60 cos 30  cos 2 60  sin 2 60  1 . Câu 2. Rút gọn P  cos 20  cos 40  .....  cos160  cos180 Lời giải P  cos 20  cos 40  .....  cos160  cos180  cos 20  cos 40  cos 60  cos80  cos100  cos120  cos140  cos160  cos180  cos 20  cos 40  cos 60  cos80  cos80  cos 60  cos 40  cos 20  cos180  cos180  1 . Câu 3. Tính giá trị biểu thức P  sin 2 10  sin 2 20  sin 2 30  ...  sin 2 80. Lời giải Do 10O  80O  20  70  30  60  40  50  90 nên các cung lượng giác tương ứng đôi một phụ nhau. Áp dụng công thức sin  90  x   cosx , ta được P   sin 2 10O  cos 2 10O    sin 2 20O  cos 2 20O    sin 2 30  cos2 30    sin 2 40  cos 2 40   1  1  1  1  4. Vậy P  4. Câu 4. Cho biểu thức      1  3  1  P  x    tan   x  .tan   x   cos   x .  sin 2  2  x   2 cos2 x  2  cos 2  x     2  sin   x         2  Rút gọn biểu thức P  x  ta được P  x   m.sin 2 x  n.cos 2 x . Tính S  m 2  n 2 ? Lời giải      1  3  1  P  x    tan   x  .tan   x   cos   x .  sin 2  2  x   2 cos2 x  2  cos 2  x     2  sin   x         2   1   1  2 2   tan x.cot x 2  cos   x  .  sin x  2 cos x  sin x 2  sin x   cot 2 x sin 2 x  2 cos 2 x  3cos 2 x. Vậy m  0 ; n  3  S  9 . Câu 5. Một chiếc đu quay có bán kính 75 m , tâm của vòng quay ở độ cao 90 m (tham khảo hình vẽ). Thời gian quay hết 1 vòng của đu quay là 30 phút. Nếu một người vào cabin tại vị trí thấp nhất của vòng quay thì sau 20 phút quay, người đó ở độ cao bao nhiêu mét? Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 9
  10. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ Lời giải Chọn vị trí xuất phát A làm mốc. Ta xét chiều quay của đu quay là theo chiều kim đồng hồ. Cứ 30 phút thì đu quay sẽ quay được 1 vòng  3600 . 20.3600 Suy ra, sau 20 phút thì đu quay sẽ quay được  2400  ở tại vị trí B theo hình vẽ. 30   BOH  600 . OH OH 75 Có cos BOH   cos 600   OH   m  . OB 75 2 75 Vậy sau 20 phút thì người đó ở độ cao 15  75   127,5 mét. 2 Câu 6. ˆ Tam giác ABC có AB  5, BC  7, CA  8 . Khi đó số đo góc A bằng bao nhiêu? Lời giải  AB  AC 2  BC 2 52  82  7 2 2 1 Theo định lí hàm cosin, ta có cos A    . 2 AB. AC 2.5.8 2 ˆ Do đó, A  60 . Câu 7. Cho tam giác ABC có B  30 , C  55 và cạnh AC  16cm . Tính cạnh AB ? Lời giải Theo định lí sin, ta có: AC AB 16 AB 16sin 55     AB   26, 2  cm  . sin B sin C sin 30 sin 55 sin 30 Câu 8. Cho tam giác ABC có B  40 , C  55 và cạnh AC  20cm . Tính cạnh BC ? Trang 10 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  11. Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Lời giải Ta có: A  180   B  C   180   40  55   85 Theo định lí sin, ta có: AC BC 20 BC 20sin 85     BC   31 cm  sin B sinA sin 40 sin 85 sin 40 Câu 9. Cho tam giác ABC có B  30 và cạnh AC  16cm . Tính bán kính đường tròn ngoại tiếp tam giác ABC? Lời giải Theo định lí sin, ta có: AC AC 16  2R  R    16  cm  sin B 2sin B 2sin 30 Câu 10. Cho tam giác ABC có B  50 và cạnh AC  20cm . Tính bán kính đường tròn ngoại tiếp tam giác ABC? Lời giải Theo định lí sin, ta có: AC AC 20  2R  R    13, 054  cm  sin B 2sin B 2sin 50 Câu 11. Cho tam giác ABC có B  35 , C  50 và cạnh AC  12cm . Tính cạnh AB ? Lời giải Theo định lí sin, ta có: AC AB 12 AB 12sin 50     AB   16, 03  cm  . sin B sin C sin 35 sin 50 sin 35 Câu 12. Cho ABC có bán kính đường tròn nội tiếp là r  4 , nửa chu vi p  10 . Diện tích tam giác ABC bằng bao nhiêu? Lời giải Diện tích tam giác ABC là S  pr  10.4  40 . Câu 13. Cho tam giác ABC có a  6, b  6, c  8 . Khi đó diện tích của tam giác bằng bao nhiêu? Lời giải 668 Nửa chu vi tam giác p   10 2 Diện tích tam giác ABC là S  10. 10  6  . 10  6  . 10  8   8 5 . Câu 14. Cho tam giác ABC có   60, AB  6, AC  8 . Tính BC . A Lời giải Áp dụng định lý Cô-sin trong tam giác ABC ta có: BC 2  AB 2  AC 2  2 AB  AC  cos A Thay số: BC 2  6 2  82  2.6.8.cos 60 Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 11
  12. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/  BC 2  36  64  48  52  BC  52  2 13 Câu 15. Tam giác ABC có AB  4, BC  6, AC  2 7 . Điểm M thuộc đoạn BC sao cho MC  2 MB . Tính độ dài AM . Lời giải  AB 2  BC 2  AC 2 16  36  28 1 Ta có: BM  2 và cos B    . 2 AB.BC 2.4.6 2  1 Vậy AM 2  AB 2  BM 2  2 AB  BM  cos B  16  4  2.4.2.  12  AM  2 3 . 2 Câu 16. Cho tam giác ABC biết a  2 3, b  2 2, c  6  2 . Số đo của góc lớn nhất của tam giác bằng bao nhiêu? Lời giải   B   do đó góc  là góc lớn nhất. Theo giả thiết ta có c  b  a suy ra C  A A Theo hệ quả của định lý Cô-sin ta có 2 2 2 cos A  b2  c 2  a 2        2 2  6 2  2 3  44 3  1 2bc   22 2  6  2 8 3 8 2 Suy ra   120 A Vậy góc lớn nhất là góc A có sổ đo là 120 .   Câu 17. Tam giác ABC có B  300 , C  450 , AB  3 . Tính cạnh AC Lời giải Theo định lí sin ta có AC AB AB sin B 3sin 300 3 2   AC    . sin B sin C sin C sin 450 2   Câu 18. Tam giác ABC có tổng hai góc B và C bằng 150 0 và BC  a . Tính bán kính đường tròn ngoại tiếp tam giác ABC Lời giải Xét ABC có   B  C  1800  A  1800  B  C  1800  1500  300 . A        Theo định lí sin ta có BC BC a  2R  R   a. sin A 2 sin A 2 sin 30 0 Câu 19. Cho tam giác ABC thoả mãn hệ thức b  c  2a . Chứng minh rằng sin B  sin C  2 sin A. Trang 12 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  13. Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Lời giải a b c Theo định lí sin ta có    2R . sin A sin B sin C a  2 R sin A   b  2 R sin B . c  2 R sin C  Ta có b  c  2a  2 R sin B  2 R sin C  2.2 R sin A.  sin B  sin C  2sin A.  Câu 20. Cho tam giác ABC biết AB  4 , AC  5 , BAC  60 . Khi đó diện tích của tam giác ABC bằng bao nhiêu? Lời giải Áp dụng công thức tính diện tích tam giác ta có: 1  1 1 3 S ABC  AB. AC .sin BAC  .4.5.sin 60  .4.5. 5 3. 2 2 2 2 Câu 21. Cho tam giác ABC biết a  7 , b  8 , c  9 . Khi đó diện tích của tam giác ABC bằng bao nhiêu? Lời giải a bc 789 Ta có: p    12 . 2 2 Áp dụng công thức Hê-rông: S ABC  p  p  a  p  b  p  c   12 12  7 12  8 12  9   12.5.4.3  12 5 .   Câu 22. Cho tam giác ABC biết a  6 , B  85 , C  65 . Khi đó bán kính đường tròn ngoại tiếp ABC bằng bao nhiêu? Lời giải Ta có:   180  B  C  180   85  65   30 . A     a a 6 Áp dụng định lý sin ta có:  2R  R   6. sin A 2 sin A 2.sin 30 Câu 23. Cho hình chữ nhật ABCD có cạnh AB  4 , BC  6 , M là trung điểm của BC , N là điểm trên cạnh CD sao cho ND  3NC . Khi đó diện tich tam giác AMN bằng bao nhiêu? Lời giải Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 13
  14. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ Cách 1: Ta có MC  3, NC  1 ; BM  3 ; ND  3 . 1 1 1 15 S AMN  S ABCD  S ABM  SMCN  S ADN  4.6  .4.3  .3.1  .3.4  2 2 2 2 Cách 2: Ta có MC  3, NC  1  MN  10 BM  3, AB  4  AM  5 AD  6, ND  3  AN  45 AM  AN  MN 10  5  45 p  2 2 15 S AMN  p  p  AM  p  AN  p  MN   2 Câu 24. Cho tam giác ABC có A  120o ; b  8; c  5. Tính bán kính đường tròn nội tiếp tam giác ABC . Lời giải Ta có a  b  c  2bc cos A  5  8  2.5.8cos120o  129  a  129 . 2 2 2 2 2 1 1 S  bc sin A  .8.5.sin120o  10 3 . 2 2 a  b  c 13  129 p  2 2 S 20 3 S  pr  r   r  p 13  129 Câu 25. Cho tam giác ABC có A  60o ; b  12; c  13. Tính đường cao lớn nhất của tam giác ABC . Lời giải Ta có a 2  b 2  c 2  2bc cos A  122  132  2.12.13cos 60o  157  a  157  12,5 . 1 1 Diện tích ABC là: S  .b.c.sin A  .12.13.sin 60  39 3 . 2 2 1 1 1 Do S  .a.ha  .b.hb  .c.hc , mà c  a  b  hc  ha  hb 2 2 2 2 S 2.39 3 13 3 hb    . b 12 2   Câu 26. Cho tam giác ABC , có A  105 , C  45 và AC  10 . Tính độ dài cạnh AB . Lời giải Ta có B  180    C  30 .  A   AB AC 10 Theo định lý sin, ta có:   AB  .sin 45  10 2 . sin C sin B sin 30 Vậy AB  10 2 . Câu 27. Cho tam giác ABC có BC  8 , CA  7 , AB  5 . Trên cạnh BC lấy điểm M sao cho BM  5 . Tính bán kính r của đường tròn nội tiếp tam giác ACM . Lời giải Trang 14 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  15. Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG AB 2  BC 2  AC 2 52  82  7 2 1  Xét tam giác ABC có: cos B     B  60 . 2 AB.BC 2.5.8 2 Xét tam giác ABM có: AB  BM  5 ;   60  ABM là tam giác đều. ABM   120 .  AM  5 , AMC 1 1 15 3 Xét tam giác ACM có: S AMC  AM .MC.sin   .5.3.sin120  AMC 2 2 4 5 3 7 15 Mặt khác SAMC  p.r  .r  .r 2 2 15 15 3 3 Suy ra: r r . 2 4 2 Câu 28. Cho tam giác ABC có AB  2 , AC  3 , BC  4 . Gọi M là trung điểm cạnh AB . Tính bán kính R của đường tròn ngoại tiếp tam giác BCM . Lời giải Xét tam giác ABC có: 2 BC 2  AC 2 AB 2 23 23 CM     CM  . 2 4 2 2 23 BM 2  BC 2  CM 2 1  16  2 11 Xét tam giác MBC có: cos B    2 BM .BC 2.1.4 16 23 BM 2  BC 2  CM 2 1  16  2 11 cos B    2 BM .BC 2.1.4 16 3 15  sin B  1  cos 2 B  (do sin B  0 ) 16 23 MC MC 4 690 Xét tam giác BMC , ta có  2R  R   2  sin B 2sin B 3 15 45 8 4 690 Vậy bán kính của đường tròn ngoại tiếp tam giác BCM là R  45 Câu 29. Để đo khoảng cách từ vị trí A đến vị trí B ở hai bên bờ một cái ao, bạn An đi dọc bờ ao từ vị trí     A đến vị trí C và tiến hành đo BAC , BCA . Biết AC  25 m, BAC  5957 ', BCA  829 ' . Hỏi khoảng cách từ vị trí A đến vị trí B là bao nhiêu mét (làm tròn kết quả đến hàng đơn vị)? Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 15
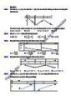
  16. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ Lời giải   5957 '; BCA  829 ' . Xét tam giác ABC , ta có: BAC     180  5957 ' 829'  3754' . ABC AB AC Áp dụng định lí sin trong tam giác ABC ta có:  sin C sin B AC.sin C 25.sin 829 '  AB    28, 6  m  . sin B sin 3754 ' Vậy khoảng cách từ vị trí A đến vị trí B là 28, 6 m . Câu 30. Bạn A đứng ở đỉnh của tòa nhà và quan sát chiếc diều, nhận thấy góc nâng (góc nghiêng giữa phương từ mắt của bạn A tới chiếc diều và phương nằm ngang) là   35 ; khoảng cách từ đỉnh tòa nhà tới mắt bạn A là 1, 5 m . Cùng lúc đó ở dưới chân tòa nhà, bạn B cũng quan sát chiếc diều và thấy góc nâng là   75 ; khoảng cách từ mặt đất đến mắt bạn B cũng là 1, 5 m . Biết chiều cao của tòa nhà là h  20 m (Hình vẽ). Chiếc diều bay cao bao nhiêu mét so mặt đất (làm tròn kết quả đến hàng đơn vị)? Lời giải Gọi các điểm: Trang 16 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  17. Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG O là vị trí của chiếc diều. H là hình chiếu vuông góc của chiếc diều trên mặt đất. C , D lần lượt là hình chiếu vuông góc của A, B trên OH . Đặt OC  x , suy ra OH  x  20  1, 5  x  21, 5  m  . OC OC x Xét tam giác OAC , ta có: tan    AC   . AC tan  tan 35 OD OD x  20 Xét tam giác OBD , ta có: tan    BD   BD tan  tan 75 x x  20 Mà: AC  BD    tan 35 tan 75 20  tan 35  x  tan 75  ( x  20)  tan 35  x   4, 6  m  . tan 75  tan 35 Suy ra OH  26,1  m  . Vậy chiếc diều bay cao 26,1 m so với mặt đất.    Câu 31. Cho M là điểm nằm trong tam giác ABC sao cho MAB  MBC  MCA   . S  SABC . Chứng minh rằng cot   cot A  cot B  cot C Lời giải Áp dụng định lí côsin trong tam giác MAB , ta có BM 2  AB2  AM 2  2 AB.AM.cos  Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 17
  18. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ 1 Mặt khác SABM  AB.AM.sin   BM 2  AB2  AM 2  4SMAB .cot  2 Tương tự ta có CM 2  BC 2  BM 2  4SMBC .cot  , AM 2  AC 2  CM 2  4SMCA .cot  Cộng vế với vế suy ra BM  CM 2  AM 2  2 AB2  AM 2  4SMAB .cot   BC 2  BM 2  4SMBC .cot   AC 2  CM 2  4SMCA .cot   AB2  BC 2  AC 2  4SMAB .cot   4SMBC .cot   4SMCA .cot   4.cot  SMAB  SMBC  SMCA   4S.cot  a2  b2  c 2  cot    cot A  cot B  cot C . 4S b2  c 2  a2 cos A 2bc b2  c 2  a 2 ( Tam giác ABC ta có cot A    sin A 2S 4S bc a  c b 2 2 2 a  b c 2 2 2 cotB  ; cotC  4S 4S a2  b2  c 2  cot A  cot B  cot C  ). 4S  Câu 32. Tam giác nhọn ABC có AC  b, BC  a , BB ' là đường cao kẻ từ B và CBB '   . Tìm công thức tính bán kính đường tròn ngoại tiếp R của tam giác ABC được tính theo a, b và  ? Lời giải  BC Xét tam giác BBC vuông tại B, có sin CBB   BC  a.sin  . BC 2 2 2 Mà AB  BC  AC  AB  b  a.sin  và BB  a .cos  . 2 Tam giác ABB vuông tại B, có AB  BB2  AB2   b  a.sin    a 2 .cos 2   b 2  2ab.sin   a 2 sin 2   a 2 cos 2   a 2  b 2  2ab sin  . Bán kính đường tròn ngoại tiếp cần tính là AB a 2  b 2  2ab sin   2R  R  . sin  ACB 2 cos  Câu 33. Cho tam giác ABC có độ dài đường trung tuyến ma , mb , , mc thỏa mãn 5ma  mb  mc2 . Khi đó tam 2 2 giác ABC là tam giác gì? Trang 18 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
  19. Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Lời giải Ta có 5ma  mb  mc2  5. 2 2  2 b  c2  a2 2   2  a 2  c2   b2  2  a 2  b2   c 2 4 4 4  10b2  10c2  5a2  2a2  2c2  b2  2a2  2b2  c 2  9b 2  9c 2  9a 2  b 2  c 2  a 2 Vậy tam giác ABC vuông tại A . sin B  sin C Câu 34. Cho tam giác ABC thỏa mãn: sin A  . Khi đó tam giác ABC là tam giác gì? cos B  cos C Lời giải Ta có: sin B  sin C sin A   sin A.  cos B  cos C   sin B  sin C cos B  cos C a  a 2  c 2  b2 a 2  b 2  c 2  b c  .    2R  2ac 2ab  2R 2R a2  c2  b2 a2  b2  c2   bc 2c 2b  b.  a 2  c 2  b 2   c.  a 2  b 2  c 2   2bc  b  c   ba 2  bc 2  b3  ca 2  cb 2  c 3  2cb 2  2bc 2  ba 2  ca 2  b3  c 3  bc 2  cb 2  0   b  c  a 2   b  c   b 2  bc  c 2    b  c  .bc  0   b  c   a 2  b 2  bc  c 2  bc   0  a 2  b 2  bc  c 2  bc  0  a2  b2  c2 . Vậy tam giác ABC vuông tại A. Câu 35. Ông X cần đo diện tích mảnh đất hình tứ giác, ông đi theo chu vi mảnh đất, lần lượt đo độ dài các cạnh và một góc như hình vẽ.Tính diện tích của mảnh đất đó(làm tròn đến m 2 ). Lời giải Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 19
  20. Blog: Nguyễn Bảo Vương: https://www.nbv.edu.vn/ Gọi mảnh đất cần tính diện tích là ABCD. Áp dụng định lí Côsin vào tam giác ABD ta có: BD  AB 2  AD 2  AB. AD cos A  58, 48 m. 1  Diện tích tam giác ABD là: S ABD  AB. AD.cos BAD  528,58 m 2 . 2 BC  BD  CD Nữa chu vi tam giác BCD là: p   86, 74 m. 2 Diện tích tam giác BCD là: S BCD  p  p  BC  p  BD  p  CD   1442,38 m 2 . Vậy diện tích mảnh đất của ông X xấp xỉ 1971 m2 . PHẦN 3. BÀI TẬP TRẮC NGHIỆM Câu 1. Cho góc    90;180 . Khẳng định nào sau đây đúng? A. sin  và cot  cùng dấu. B. Tích sin  .cot  mang dấu âm. C. Tích sin  .cos  mang dấu dương. D. sin  và tan  cùng dấu. Câu 2. Giá trị của cos 30  sin 60 bằng bao nhiêu? 3 3 A. . B. . C. 3. D. 1. 3 2 Câu 3. Cho góc  tù. Điều khẳng định nào sau đây là đúng? A. sin   0 . B. cos   0 . C. tan   0 . D. cot   0 . 1 Câu 4. Cho sin   , với 90    180 . Tính cos  . 3 2 2 2 2 2 2 A. cos   . B. cos    . C. cos   . D. cos    . 3 3 3 3 1 Câu 5. Cho cos x  . Tính biểu thức P  3sin 2 x  4cos2 x 2 13 7 11 15 A. . B. . C. . D. . 4 4 4 4 1 Câu 6. Biết  là một góc từ 0 o đến 180o thỏa mãn cos   . Tính sin  . 3 Trang 20 Fanpage Nguyễn Bảo Vương  https://www.facebook.com/tracnghiemtoanthpt489/
ADSENSE

CÓ THỂ BẠN MUỐN DOWNLOAD

THÔNG TIN
TRỢ GIÚP
HỖ TRỢ KHÁCH HÀNG
Theo dõi chúng tôi

Chịu trách nhiệm nội dung:

Nguyễn Công Hà - Giám đốc Công ty TNHH TÀI LIỆU TRỰC TUYẾN VI NA

LIÊN HỆ

Địa chỉ: P402, 54A Nơ Trang Long, Phường 14, Q.Bình Thạnh, TP.HCM

Hotline: 093 303 0098

Email: support@tailieu.vn

Giấy phép Mạng Xã Hội số: 670/GP-BTTTT cấp ngày 30/11/2015 Copyright ©2025 TaiLieu.VN. All rights reserved.

 

Đồng bộ tài khoản
48=>0