TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG Điện thoại: 0946798489
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuong Trang 1
PHẦN 1. LÝ THUYẾT – VÍ DỤ
CHƯƠNG IX. TÍNH XÁC SUẤT THEO ĐỊNH NGHĨA CỔ ĐIỂN
BÀI 26. BIẾN CỐ VÀ ĐỊNH NGHĨA CỔ ĐIỂN CỦA XÁC SUẤT
A - Kiến thức cần nhớ
- Phép thử ngẫu nhiên (gọi tắt là phép thử) là một thí nghiệm hay một hành động mà kết quả của nó không
thể biết trước đượcc. Tập hợp tất cả các kết quả có thể xảy ra khi thực hiện phép thử được gọi là không gian
mẫu của phép thử và kí hiệu là
.
- Kết quả của phép thử làm cho biến cố
E
xảy ra gọi là kết quả thuận lợi cho
E
. Biến cố
E
là một tập con
của không gian mẫu
, bao gồm tất cả các kết quả thuận lợi cho
E
.
- Biến cố đối của biến cố
E
là biến cố: “E không xảy ra" và được kí hiệu là E. Đó là phần bù của
E
trong
.
- Cho phép thử
T
có không gian mẫu là
với các kết quả có thể của
T
là đồng khả năng. Nếu
E
là một
biến cố liên quan đến phép thử
T
thì xác suất của
E
được cho bởi công thức ( )
( ) ,
( )
n E
P E n
tức là xác suất của
E
bằng tỉ số giữa số kết quả thuận lợi của
E
và số kết quả có thể.
- Nếu biến cố
E
có xác suất là
( )P E
thì khi thực hiện phép thử
n
lần
( 30)n
, thì số lần xuất hiện biến cố
E
sẽ xấp xỉ bằng
( )nP E
(n càng lớn thì sai số tương đối càng bé).
B - Ví dụ
Ví dụ 1. Một túi có chứa 3 viên bi xanh, 4 viên bi đỏ, 5 viên bi đen và 6 viên bi trắng. Lấy ngẫu nhiên một
viên bi từ trong túi.
a) Mô tả không gian mẫu.
b) Gọi
H
là biến cố "Bi rút ra có màu đỏ". Các biến cố
H
và H là các tập con nào của không gian mẫu?
c) Gọi
K
là biến cố "Bi rút ra có màu xanh hoặc màu trắng". Các biến cố
K
và K là các tập con nào của
không gian mẫu?
Giải
Kí hiệu 3 viên bi xanh là
1 2 3
, , ;4X X X
viên bi đỏ là
1 2 3 4
, , , ;5D D D D
viên bi đen là
1 2 3 4 5
, , , ,B B B B B
, và 6
viên bi trắng là
1 2 3 4 5 6
, , , , ,T T T T T T
. Ta có
a)
1 2 3 1 2 3 4 1 2 3 4 5 1 2 3 4 5 6
; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; ; X X X D D D D B B B B B T T T T T T
.
b)
1 2 3 4
; ; ;H D D D D
.
1 2 3 1 2 3 4 5 1 2 3 4 5 6
; ; ; ; ; ; ; ; ; ; ; ; ;H X X X B B B B B T T T T T T
.
c)
1 2 3 1 2 3 4 5 6
; ; ; ; ; ; ; ;K X X X T T T T T T
.
1 2 3 4 1 2 3 4 5
; ; ; ; ; ; ; ;K D D D D B B B B B
Ví dụ 2. Xếp ngẫu nhiên 3 bạn An, Bình, Cường đứng thành một hàng dọc. Tính xác suất để
a) An không đứng cuối hàng;
b) Bình và Cường đứng cạnh nhau;
c) An đứng giữa Bình và Cường;
d) Bình đứng trước An.
Giải
Kí hiệu
, ,A B C
tương ứng là An, Bình, Cường. Ta có
{ ; ; ; ; ; } ABC ACB BCA BAC CAB CBA
. Vậy
( ) 6 n
.
a) Gọi
E
là biến cố đang xét. Ta có
{ ; ; ; }, ( ) 4 E ABC BAC CAB ACB n E
.
Vậy
4 2
( ) 6 3
P E
.
b) Gọi
F
là biến cố đang xét. Ta có
{ ; ; ; }, ( ) 4 F ABC ACB BCA CBA n F
.
ÔN TẬP CHƯƠNG 9.
TÍNH XÁC SUẤT THEO ĐỊNH NGHĨA CỔ ĐIỂN
•TOÁN 10
•|FanPage: Nguyễn Bảo Vương
Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 2 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Vậy
4 2
( ) 6 3
P F
.
c) Gọi
G
là biến cố đang xét. Ta có
{ ; }, ( ) 2 G BAC CAB n G
.
Vậy
2 1
( ) 6 3
P G
.
d) Gọi
H
là biến cố đang xét. Ta có
{ ; ; }, ( ) 3 H BAC BCA CBA n H
.
Vậy
3 1
( ) 6 2
P H
.
BÀl 27. THỰC HÀNH TÍNH XÁC SUẤT THEO ĐỊNH NGHĨA CỔ ĐIỂN
A - Kiến thức cần nhớ
- Trong nhiều bài toán, để tính số phần tử của không gian mẫu và biến cố ta sử dụng phương pháp tổ hợp
như: các quy tắc đếm, các công thức tính số hoán vị, chỉnh hợp và tổ hợp.
- Trong một số bài toán, phép thử được hình thành từ một vài phép thử. Khi đó để có thể mô tả đầy đủ, trực
quan không gian mẫu và biến cố, ta sử dụng sơ đồ hình cây.
- Cho
E
là một biến cố. Xác suất của biến cố đối E liên hệ với xác suất của
E
bởi công thức sau:
( ) 1 ( ).P E P E
Trong một số bài toán, nếu tính trực tiếp xác suất của một biến cố gặp khó khăn, ta có thể tính gián tiếp bằng
cách tính xác suất biến cố đối của nó.
B - Ví dụ
Ví dụ 1. Một hộp đựng 30 tấm thẻ đánh số từ 1 đến 30. Chọn ngẫu nhiên 10 tấm thẻ. Tính xác suất để trong
đó có 5 số chia hết cho 3 và 5 số không chia hết cho
3.
Giải. Ta có
10
30
( ) n C
.
Gọi
E
là biến cố "Trong 10 số có 5 số chia hết cho 3 và 5 số không chia hết cho 3 ". Trong tập
{1;2; ;30}
có 10 số chia hết cho 3 và 20 số không chia hết cho 3. Vậy có
5
10
C
cách chọn 5 số chia hết cho 3 từ 10 số
chia hết cho 3 ; có
5
20
C
cách chọn 5 số không chia hết cho 3 từ 20 số không chia hết cho 3 . Theo quy tắc
nhân, ta có
5 5
10 20
( ) n E C C
.
Vậy
5 5
10 20
10
30
( ) 0,13
C C
P E C
.
Ví dụ 2. Gieo một đồng tiền cân đối ba lần.
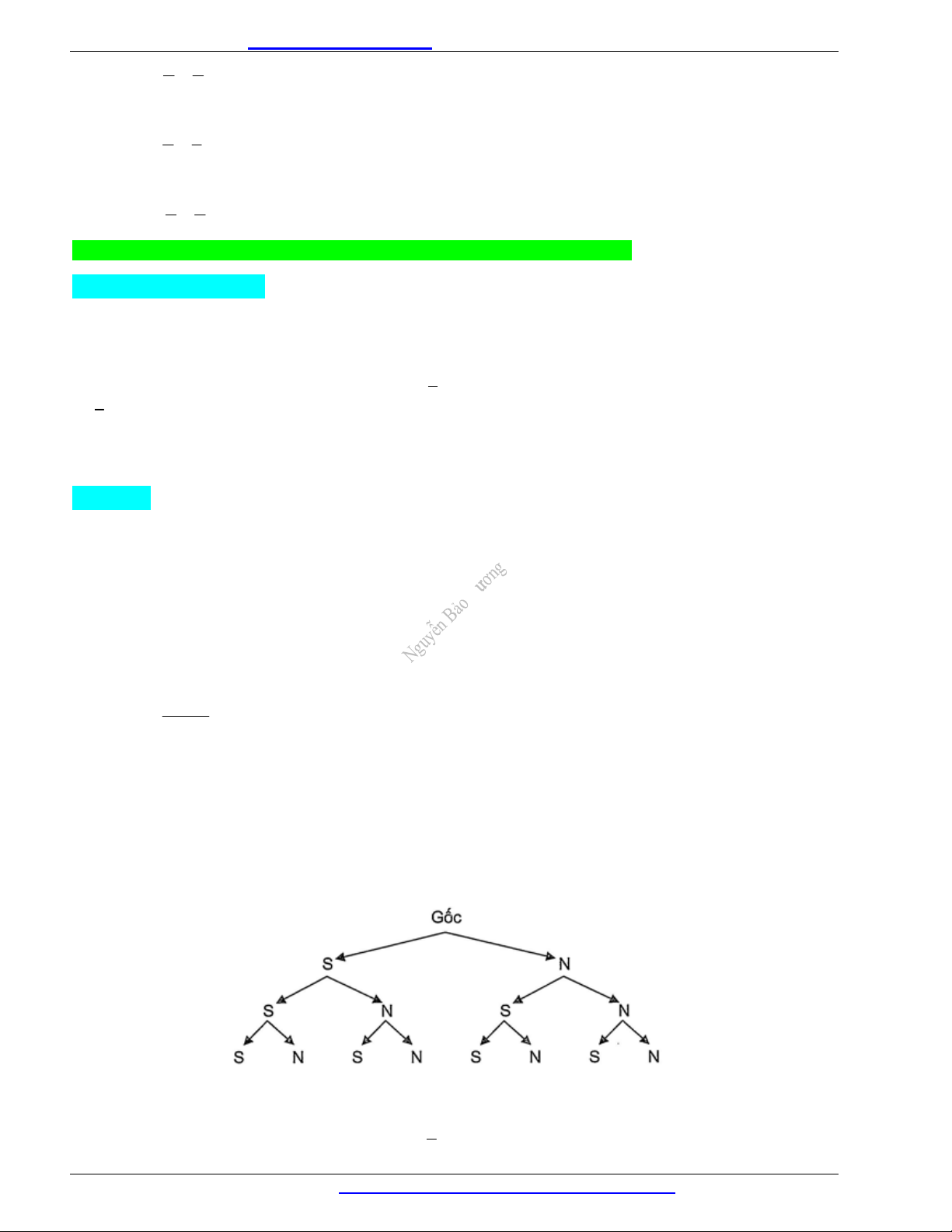
a) Vẽ sơ đồ hình cây mô tả các phần tử của không gian mẫu.
b) Tính xác suất của các biến cố:
A: "Trong ba lần gieo có hai lần sấp, một lần ngửa";
B: "Trong ba lần gieo có ít nhất một lần sấp".
Giải
a) Kí hiệu S là đồng tiền ra mặt sấp,
N
là đồng tiền ra mặt ngửa.
Ta có sơ đồ hình cây:
Các nhánh cây là: SSS, SSN, SNS, SNN, NSS, NSN, NNS, NNN.
Vậy
{
SSS; SSN; SNS; SNN; NSS; NSN; NNS; NNN
}, ( ) 8 n
.
b)
{A
SSN; SNS; NSS
}, ( ) 3n A
. Vậy
3
( ) 8
P A
.

Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 3
{ ; ; ; ; ; ; }, ( ) 7
B SSS SSN SNS SNN NSS NSN NNS n B
. Vậy
7
( )
8
P B
.
Ví dụ 3. Gieo ba con xúc xắc cân đối. Tính xác suất để có ít nhất một con xúc xắc xuất hiện mặt 6 chấm.
Giải
Gọi
E
là biến cố "Có ít nhất một con xúc xắc xuất hiện mặt 6 chấm".
Ta có
{( ; ; ),1 , , 6}
a b c a b c
. Theo quy tắc nhân
( ) 6 6 6 216
n
.
Tuy nhiên khó kiểm đếm trực tiếp được
( )n E
. Ta chuyển qua tính xác suất của biến cố đối.
Ta có
E
: “Không có con xúc xắc nào xuất hiện mặt 6 chấm" là biến cố đối của
E
.
{( ; ; ),1 , , 5}
E i j k i j k
. Theo quy tắc nhân
( ) 5 5 5 125
n E
.
125
( )
216
P E
.
Do đó
125 91
( ) 1 ( ) 1
216 216
P E P E
.
PHẦN 2. BÀI TẬP TỰ LUẬN
ĐỀ BÀI
Câu 1. Trong thực đơn của một nhà hàng có
10
món ăn mặn,
8
món ăn nhẹ và
7
thứ nước uống. Chọn
ngẫu nhiên
1
món ăn mặn,
1
món ăn nhẹ và
1
đồ uống. Tính số phần tử của không gian mẫu, biết
rằng trong tất cả các món ăn và đồ uống của nhà hàng đó không có món nào kị món nào.
Câu 2. Một hộp chứa
10
bút bi khác nhau gồm
5
bút bi màu xanh,
3
bút bi màu đen và
2
bút bi màu
đỏ. Chọn ngẫu nhiên đồng thời
2
bút từ hộp đó. Có bao nhiêu kết quả có thể xảy ra?
Câu 3. Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Tìm xác suất để trong ba lần gieo có đúng
hai lần xuất hiện mặt sấp
Câu 4. Một hộp chứa 2 bi xanh, 3 bi đỏ và 4 bi đen. Chọn ngẫu nhiên 3 bi trong hộp. Gọi A là biến cố để
3 viên bi gồm ít nhất 2 màu khác nhau. Số phần tử của biến cố A ?
Câu 5. Cho bài toán: “Gọi S là tập hợp tất cả các số tự nhiên gồm ba chữ số phân biệt được chọn từ các
chữ số 1; 2; 3; 4; 5; 6; 7. Chọn ngẫu nhiên một số từ S. Số phần tử không gian mẫu bằng bao
nhiêu?
Câu 6. Cho bài toán: “Từ các chữ số 1; 2; 3; 4; 5; 6, người ta lập tất cả các số gồm 4 chữ số đôi một khác
nhau. Chọn ngẫu nhiên một số trong các số lập được. Số phần tử không gian mẫu bằng bao nhiêu?
Câu 7. Cho bài toán: “Cho tập hợp
0; 1; 2; 3; 4; 5
A
. Gọi
S
là tập hợp các số có
2
chữ số khác
nhau được lập thành từ các chữ số của tập
A
. Chọn ngẫu nhiên một số từ
S
. Số phần tử không
gian mẫu của bằng bao nhiêu?
Câu 8. Một con súc sắc được gieo ba lần. Quan sát số chấm xuất hiện. Gọi
A
là biến cố: ‘‘Số chấm trong
lần gieo thứ nhất bằng tổng các số chấm của lần gieo thứ hai và thứ ba’’. Tính số kết quả thuận lợi
của biến cố
A
.
Câu 9. Có 100 tấm thẻ được đánh số từ 1 đến 100. Các tấm thẻ có kích thước và khối lượng như nhau.
Lấy ngẫu nhiên 5 thẻ. Tính số phần tử của biến cố
A
: “Số ghi trên các tấm thẻ được chọn là số
chẵn”.
Câu 10. Một hộp đựng 10 tấm thẻ được đánh số từ 1 đến 10. Các tấm thẻ có kích thước và khối lượng như
nhau. Chọn ngẫu nhiên 3 thẻ. Gọi
A
là biến cố “Tổng số của 3 thẻ được chọn không vượt quá 8.
Số phần tử của biến cố
A
bằng bao nhiêu?
Câu 11. Từ một hộp chứa 5 tấm thẻ được đánh số 1, 2, 3, 4, 5. Lấy ngẫu nhiên liên tiếp 2 lần mỗi lần 1 thẻ
và xếp theo thứ tự từ trái sang phải. Gọi
A
là biến cố “Chữ số sau lớn hơn chữ số trước”. Số phần
tử của biến cố
A
bằng bao nhiêu?
Câu 12. Một hộp có 25 quả bóng được đánh số từ 1 đến 25. Lấy ngẫu nhiên 1 bóng. Tính xác suất để số
ghi trên bóng là số chẵn
Câu 13. Một hộp đựng 9 quả bóng, trong đó có 4 quả màu đỏ, 5 quả màu xanh. Lấy ngẫu nhiên 3 quả.
Tính xác suất lấy được 3 quả màu đỏ
Câu 14. Một hộp bóng đèn có 7 bóng, trong đó có 5 bóng tốt. Lấy ngẫu nhiên 2 bóng. Tính xác suất để lấy
được đúng 1 bóng tốt
Câu 15. Một nhóm có
5
học sinh nam và
4
học sinh nữ. Giáo viên gọi
4
học sinh lên bảng giải bài tập.
Tính xác suất để
4
học sinh được gọi có cả nam và nữ.

Blog: Nguyễn Bảo Vương:
https://www.nbv.edu.vn/
Trang 4 Fanpage Nguyễn Bảo Vương https://www.facebook.com/tracnghiemtoanthpt489/
Câu 16. Thùng thứ nhất có 5 hộp quà đựng quần và 3 hộp quà đựng áo. Thùng thứ hai có 4 hộp quà đựng
quần và 6 hộp quà đựng áo. Các hộp quà có kích thước và khối lượng như nhau. Lấy ngẫu nhiên
từ mỗi thùng 2 hộp. Không gian mẫu của phép thử bằng bao nhiêu?
Câu 17. Một cửa hàng trong ngày khai trương có
5
món khác nhau từ thịt gà,
7
món khác nhau từ thịt
trâu và
6
món khác nhau từ thịt bò. Một khách hàng may mắn được bốc thăm
2
món miễn phí.
Tính số phần tử của biến cố: “ Người đó bốc thăm được
2
món thịt khác loại”.
Câu 18. Một quán nước có nhóm nước uống là trà, sinh tố và sữa chua trong đó trà có
6
loại, sinh tố có
9
loại và sữa chua có
7
loại. Ba người bạn vào quán gọi mỗi nguời một thứ. Tính số phần tử của
biến cố: “ Ba người đó gọi đúng hai trong ba nhóm trà, sinh tố và sữa chua”.
Câu 19. Một hộp chứa
11
bút bi khác nhau gồm
5
bút màu xanh và
6
bút màu đỏ. Chọn ngẫu nhiên đồng
thời
2
bút từ hộp đó. Tính xác suất để
2
bút chọn ra cùng màu bằng.
Câu 20. Có
13
cây bút chì phân biệt trong đó có một cây khắc chữ KIÊN, một cây khắc chữ TRÌ, một cây
khắc chữ HỌC, một cây khắc chữ TẬP, một cây khắc chữ SẼ, một cây khắc chữ THÀNH, một
cây khắc chữ CÔNG và sáu cây khắc số từ
1
đến
6
. Lấy ngẫu nhiên từ đó ra
7
cây bút chì. Tính
xác suất để rút được
7
cây bút có ghi chữ: KIÊN, TRÌ, HỌC, TẬP, SẼ, THÀNH, CÔNG.
Câu 21. Bạn Hòa gieo liên tiếp một con súc sắc và một đồng xu.Tính xác suất của biến cố
A
: “Đồng xu
xuất hiện mặt ngửa hoặc số chấm xuất hiện trên con xúc xắc là
1
”.
Câu 22. Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Tìm xác suất để trong ba lần gieo có ít
nhất một lần xuất hiện mặt sấp
Câu 23. Một hộp đựng 6 viên bi được đánh số từ 1 đến 6. Lấy ngẫu nhiên 3 viên bi rồi cộng các số trên
viên bi lại với nhau. Tính xác suất để kết quả thu được là một số không chia hết cho 8.
Câu 24. Túi I chứa 3 bi trắng, 7 bi đỏ, 15 bi xanh. Túi II chứa 10 bi trắng, 6 bi đỏ, 9 bi xanh. Từ mỗi túi
lấy ngẫu nhiên 1 viên bi. Tính xác suất để lấy được hai viên khác màu.
Câu 25. Cho bài toán: “Gọi
S
là tập hợp các số có
2
chữ số chia hết cho 3. Chọn ngẫu nhiên một số từ
S
,
tính xác suất để số được chọn là số chẵn”. Số phần tử không gian mẫu của bài toán bằng bao
nhiêu?
Câu 26. Có 20 tấm thẻ được đánh số từ 1 đến 20. Các tấm thẻ có kích thước và khối lượng như nhau. Chọn
ngẫu nhiên ra 8 tấm thẻ, tính xác suất để có 3 tấm thẻ mang số lẻ, 5 tấm thẻ mang số chẵn trong
đó chỉ có đúng một tấm thẻ mang số chia hết cho 10.
Câu 27. Một hộp có 12 quả cầu giống nhau, trong đó có 7 quả cầu trắng và 5 quả cầu đen. Lấy ngẫu nhiên
3 quả. Tính xác suất để trong 3 quả chọn ra có ít nhất hai quả màu trắng.
Câu 28. Một nhóm có
3
bạn nam và
3
bạn nữ. Chọn ngẫu nhiên
3
bạn trong nhóm đó. Tính xác suất để
trong cách chọn đó có ít nhất
1
bạn nữ.
Câu 29. Một cửa hàng có 4 áo phông, 3 áo sơ mi, 5 áo len. Hỏi có bao nhiêu cách xếp các loại áo trên
thành một dãy sao cho 4 áo phông đứng cạnh nhau, 3 áo sơ mi đứng cạnh nhau?
Câu 30. Ban chỉ đạo phòng chống dịch Covid-19 của sở y tế Bắc Ninh gồm
12
người, trong đó có đúng
bốn bác sĩ. Chia ngẫu nhiên Ban đó thành ba tổ, mỗi tổ bốn người để đi kiểm tra công tác phòng
dịch ở ba địa phương trong tỉnh. Trong mỗi tổ chọn ngẫu nhiên một người làm tổ trưởng. Số khả
năng sao cho ba tổ trưởng đều là bác sĩ bằng bao nhiêu?
Câu 31. Gọi
S
là tập hợp tất cả các số tự nhiên gồm 3 chữ số. Chọn ngẫu nhiên một số thuộc
S
. Có bao
nhiêu khả năng số chọn được có chữ số đứng sau không bé hơn chữ số đứng trước?
Câu 32. Một hộp chứa
12
bút bi khác nhau gồm
4
bút màu xanh,
5
bút màu đen và
3
bút màu đỏ. Lấy
lần lượt
2
bút từ hộp đó.Tính xác suất để bút thứ
2
màu xanh
Câu 33. Một hộp đựng tám cục tẩy được ghi số từ
1
đến
8
. Lấy ngẫu nhiên từ hộp đó
3
cục tẩy. Tính xác
suất để tổng các số ghi trên ba cục tẩy đó chia hết cho
3
.
Câu 34. Có
8
bạn cùng ngồi xung quanh một cái bàn tròn, mỗi bạn cầm một đồng xu như nhau. Tất cả
8
bạn cùng tung đồng xu của mình, bạn có đồng xu ngửa thì đứng, bạn có đồng xu sấp thì ngồi.
Tính xác suất để không có hai bạn liền kề cùng đứng
Câu 35. Trong một căn nhà có hai phòng nghỉ ngơi X, Y (mỗi phòng có thể chứa được tối đa 3 người). Ba
bạn Sơn, Hải, Văn mỗi bạn chọn ngẫu nhiên một phòng để nghỉ. Tính xác suất của biến cố “cả ba
bạn vào cùng phòng”.
Câu 36. Một chiếc hộp đựng
7
viên bi màu xanh,
6
viên bi màu đen,
5
viên bi màu đỏ,
4
viên bi màu
trắng. Chọn ngẫu nhiên ra
4
viên bi, tính xác suất để lấy được ít nhất
2
viên bi cùng màu

Điện thoại: 0946798489 TOÁN 10-KẾT NỐI TRI THỨC VỚI CUỘC SỐNG
Facebook Nguyễn Vương https://www.facebook.com/phong.baovuongTrang 5
Câu 37. Gọi
A
là tập hợp các số tự nhiên có chín chữ số đôi một khác nhau. Chọn ngẫu nhiên một số tự
nhiên thuộc vào tập
A
. Gọi biến cố
X
“ Chọn được một số thuộc
A
và số đó chia hết cho
3
”.
Tính
P X
Câu 38. Gieo
3
con súc sắc cân đối và đồng chất, kết quả là một bộ thứ tự
; ;x y z
với
; ;x y z
lần lượt là
số chấm xuất hiện trên mỗi con súc sắc. Tính xác suất để
15
x y z
.
Câu 39. Một túi đựng 10 tấm thẻ được đánh số từ 1 đến 10. Các tấm thẻ có kích thước và khối lượng như
nhau. Rút ngẫu nhiên 3 tấm thẻ từ túi đó. Tính xác suất để tổng số ghi trên ba thẻ rút được là một
số chia hết cho 3
Câu 40. Chia ngẫu nhiên 9 quả bóng gồm 4 quả màu đỏ và 5 quả màu vàng có cùng kích thước thành ba
phần, mỗi phần 3 quả. Tính xác suất để không có phần nào gồm 3 bóng cùng màu
Câu 41. Xếp
6
học sinh nam và
4
học sinh nữ vào một cái bàn tròn. Tính xác suất để có ít nhất
2
học sinh
nữ ngồi cạnh nhau.
LỜI GIẢI THAM KHẢO
Câu 1. Trong thực đơn của một nhà hàng có
10
món ăn mặn,
8
món ăn nhẹ và
7
thứ nước uống. Chọn
ngẫu nhiên
1
món ăn mặn,
1
món ăn nhẹ và
1
đồ uống. Tính số phần tử của không gian mẫu, biết
rằng trong tất cả các món ăn và đồ uống của nhà hàng đó không có món nào kị món nào.
Lời giải
Số phần tử của không gian mẫu là
10.8.7 560
(cách).
Câu 2. Một hộp chứa
10
bút bi khác nhau gồm
5
bút bi màu xanh,
3
bút bi màu đen và
2
bút bi màu đỏ. Chọn
ngẫu nhiên đồng thời
2
bút từ hộp đó. Có bao nhiêu kết quả có thể xảy ra?
Lời giải
Số cách lấy ra
2
bút trong
10
bút là
2
10
C
, Suy ra
2
10
45
n C
.
Câu 3. Gieo một đồng xu cân đối và đồng chất liên tiếp ba lần. Tìm xác suất để trong ba lần gieo có đúng hai lần
xuất hiện mặt sấp
Lời giải
Kí hiệu
S
và
N
tương ứng là đồng xu ra mặt sấp và đồng xu ra mặt ngửa. Khi đó không gian mẫu là
, , ; , , ; , , ; , , ; , , ; , , ; , , ; , ,
S S S S S N S N S S N N N S S N S N N N S N N N
.
Ta có
8
n
.
Gọi
A
là biến cố trong ba lần gieo có đúng hai lần xuất hiện mặt sấp. Ta có
, , ; , , ; , ,A S S N S N S N S S
. Ta có
3
n A
.
Vậy xác suất của biến cố
A
là
3
8
P A
.
Câu 4. Một hộp chứa 2 bi xanh, 3 bi đỏ và 4 bi đen. Chọn ngẫu nhiên 3 bi trong hộp. Gọi A là biến cố để 3 viên bi
gồm ít nhất 2 màu khác nhau. Số phần tử của biến cố A ?
Lời giải
Xét biến cố
A
= “3 viên bi lấy ra cùng chỉ có 1 màu”.
3 3 3
3 4 9
5 5 79
n A C C n A C
.
Câu 5. Cho bài toán: “Gọi S là tập hợp tất cả các số tự nhiên gồm ba chữ số phân biệt được chọn từ các chữ số 1; 2;
3; 4; 5; 6; 7. Chọn ngẫu nhiên một số từ S. Số phần tử không gian mẫu bằng bao nhiêu?
Lời giải
Xếp
7
số đã cho vào 3 vị trí
abc
có
3
7
210
A
cách nên số phần tử không gian mẫu là
210.





![Bài tập so sánh hơn và so sánh nhất của tính từ [kèm đáp án/mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250808/nhatlinhluong27@gmail.com/135x160/77671754900604.jpg)
![Tài liệu tham khảo Tiếng Anh lớp 8 [mới nhất/hay nhất/chuẩn nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250806/anhvan.knndl.htc@gmail.com/135x160/54311754535084.jpg)




![Tài liệu Lý thuyết và Bài tập Tiếng Anh lớp 6 [Mới nhất]](https://cdn.tailieu.vn/images/document/thumbnail/2025/20250802/hoihoangdang@gmail.com/135x160/18041754292798.jpg)




