
1
BAØI GIAÛNG TOÙM TAÉT
MOÂN TOAÙN C2
(GV: Traàn Ngoïc Hoäi - 2009)
CHÖÔNG 1
MA TRAÄN
HEÄ PHÖÔNG TRÌNH TUYEÁN TÍNH
A. MA TRAÄN
§1. ÑÒNH NGHÓA VAØ KYÙ HIEÄU
1.1. Ñònh nghóa:
Moät ma traän loaïi m × n treân R laø moät baûng chöõ nhaät goàm m doøng, n coät vôùi
mn heä soá thöïc coù daïng:
11 12 1n
21 22 2n
m1 m2 mn
a a ... a
aa...a
A..... ...... ... ......
a a ... a
⎛⎞
⎜⎟
⎜⎟
=⎜⎟
⎜⎟
⎝⎠
Vieát taét: A = (aij)m×n hay A = (aij), trong ñoù aij ∈ R.
Ta goïi:
aij : heä soá ôû doøng i, coät j cuûa ma traän A;
m : soá doøng cuûa ma traän A;
n : soá coät cuûa ma traän A;
(ai1 ai2 ... ain) : doøng thöù i cuûa ma traän A;
2
1j
2j
mj
a
a
a
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
: coät thöù j cuûa ma traän A.
Kyù hieäu: Mm×n (R) laø taäp hôïp taát caû nhöõng ma traän loaïi m×n treân R.
Ví duï: 32
M
210
321
A×
∈
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
=(R); 23
M
32
10
21
B×
∈
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
=(R)
1.2. Ñònh nghóa:
Cho hai ma traän cuøng loaïi A = (aij)m×n vaø B = (bij)m×n. Ta noùi A baèng B, kyù
hieäu A = B, neáu aij = bij, ∀1 ≤ i ≤m, 1 ≤ j ≤ n.
1.3. Ñònh nghóa:
(i) Ma traän khoâng loaïi m × n, kyù hieäu: 0m×n hay 0, laø ma traän loaïi m × n maø taát
caû caùc heä soá ñeàu baèng 0.
(ii) Moät ma traän vuoâng caáp n laø moät ma traän loaïi n × n (i.e. soá doøng = soá coät = n).
Trong moãi ma traän vuoâng caáp coù moät ñöôøng cheùo chính (goïi taét laø ñöôøng
cheùo) goàm caùc heä soá aii, 1 ≤ i ≤ n.
Taäp caùc ma traän vuoâng caáp n treân R ñöôïc kyù hieäu laø Mn(R).
(iii) Moät ma traän cheùo caáp n laø moät ma traän vuoâng caáp n maø taát caû caùc heä soá
naèm ngoaøi ñöôøng cheùo chính ñeàu baèng 0.
11
22
nn
a 0 ... 0
0a...0
A........................
00...a
⎛⎞
⎜⎟
⎜⎟
=⎜⎟
⎜⎟
⎝⎠
(iv) Ma traän ñôn vò caáp n, kyù hieäu In hay I, laø ma traän cheùo caáp n maø taát caû caùc
heä soá naèm treân ñöôøng cheùo chính ñeàu baèng 1:
Printed with FinePrint trial version - purchase at www.fineprint.com
Vuihoc24h.vn

3
nijnn
10...0
0 1 ... 0
I()
.....................
01
×
⎛⎞
⎜⎟
⎜⎟
==δ
⎜⎟
⎜⎟
⎝⎠
vôùi ⎩
⎨
⎧
≠
=
=δ jineáu0
jineáu1
ij
(v) Moät ma traän tam giaùc treân (tam giaùc döôùi) caáp n laø moät ma traän vuoâng caáp n
maø taát caû caùc heä soá naèm phía döôùi (phía treân) ñöôøng cheùo chính ñeàu baèng 0.
Nhö vaäy,
A = (aij)n×n laø ma traän tam giaùc treân
⇔ aij = 0, ∀1 ≤ j < i ≤ n, nghóa laø A coù daïng:
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
nn
n222
n11211
a...00
.............................
a...a0
a...aa
A
B = (bij)n×n laø ma traän tam giaùc döôùi
⇔ bij = 0, ∀1 ≤ i < j ≤ n, nghóa laø B coù daïng:
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
nn2n1n
2221
11
b...bb
............................
0...bb
0...0b
B
§2. CAÙC PHEÙP TOAÙN MA TRAÄN
2.1. Pheùp laáy chuyeån vò:
Cho A = (aij) laø moät ma traän loaïi m×n. Ta goïi ma traän chuyeån vò cuûa A, kyù
hieäu AT, laø ma traän loaïi n×m, coù ñöôïc töø A baèng caùch xeáp caùc doøng cuûa A thaønh
caùc coät töông öùng cuûa AT. Nghóa laø:
11 12 1n 11 21 m1
21 22 2n 12 22 m2
T
m1 m2 mn 1n 2n mn
aa...a aa...a
a a ... a a a ... a
AA
............................ ...........................
a a ... a a a ... a
⎛⎞⎛⎞
⎜⎟⎜⎟
⎜⎟⎜⎟
=⇒=
⎜⎟⎜⎟
⎜⎟⎜⎟
⎝⎠⎝⎠
Nhö vaäy, heä soá ôû doøng i, coät j cuûa ma traän AT baèng heä soá ôû doøng j, coät cuûa ma
traän A.
4
2.2. Pheùp nhaân voâ höôùng:
Cho ma traän A = (aij)m×n vaø soá thöïc α ∈ R. Ta ñònh nghóa αA laø ma traän coù
töø A baèng caùch nhaân taát caû caùc heä soá cuûa A cho α, nghóa laø:
αA = (αaij)m×n
Ví duï:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−620
286
310
143
2
Kyù hieäu: – A = (–1)A = (– aij)m×n
Ta deã daøng kieåm tra ñöôïc caùc tính chaát sau:
Vôùi A = (aij) vaø α, β ∈ R;
(i) (αβ)A = α(βA)
(ii) (αA)T = αAT
(iii) 0.A = 0 vaø 1.A = A.
2.3. Pheùp coäng ma traän:
Cho hai ma traän cuøng loaïi m×n: A = (aij)m×n vaø = (bij)m×n. Ta ñònh nghóa toång
hai ma traän A vaø B, kyù hieäu A + B, laø ma traän loaïi m×n maø caùc heä soá coù ñöôïc
baèng caùch laáy toång cuûa caùc heä soá töông öùng cuûa A vaø B, nghóa laø:
A + B = (aij + bij)m×n
Ví duï:
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
=
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−
−
+
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
−6108
433
387
401
321
032
Ta deã daøng kieåm ñöôïc caùc tính chaát sau:
Vôùi A, B, C ∈ Mm×n(R) vaø α, β ∈ R ta coù:
(i) A + B = B + A (tính giao hoaùn);
(ii) (A + B) + C = A + (B + C) (tính keát hôïp);
(iii) 0m×n + A = A + 0m×n = A;
(iv) A + (–A) = (–A) + A = 0m×n;
(v) (A + B)T = AT + BT;
(vi) α(A + B) = αA + αB
(vii) (α + β)A = αA + βA;
(viii) (–α)A = α(–A) = –(αA)
Printed with FinePrint trial version - purchase at www.fineprint.com
Vuihoc24h.vn
5
Kyù hieäu: A – B = A + (–B) = (aij – bij)m×n
2.4. Pheùp nhaân ma traän:
Cho hai ma traän A vaø B coù tính chaát: Soá coät cuûa ma traän A baèng soá doøng cuûa
ma traän B. Cuï theå ma traän A = (aij) loaïi m×n vaø ma traän B = (bij) loaïi n×p. Ta
ñònh nghóa tích cuûa hai ma traän A vaø B, kyù hieäu AB, laø ma traän C loaïi m×p ñònh
bôûi:
• Veà loaïi: C coù loaïi m×p.
[Ghi nhôù baèng kyù hieäu hình thöùc : (m×n)(n×p)= (m×p)]
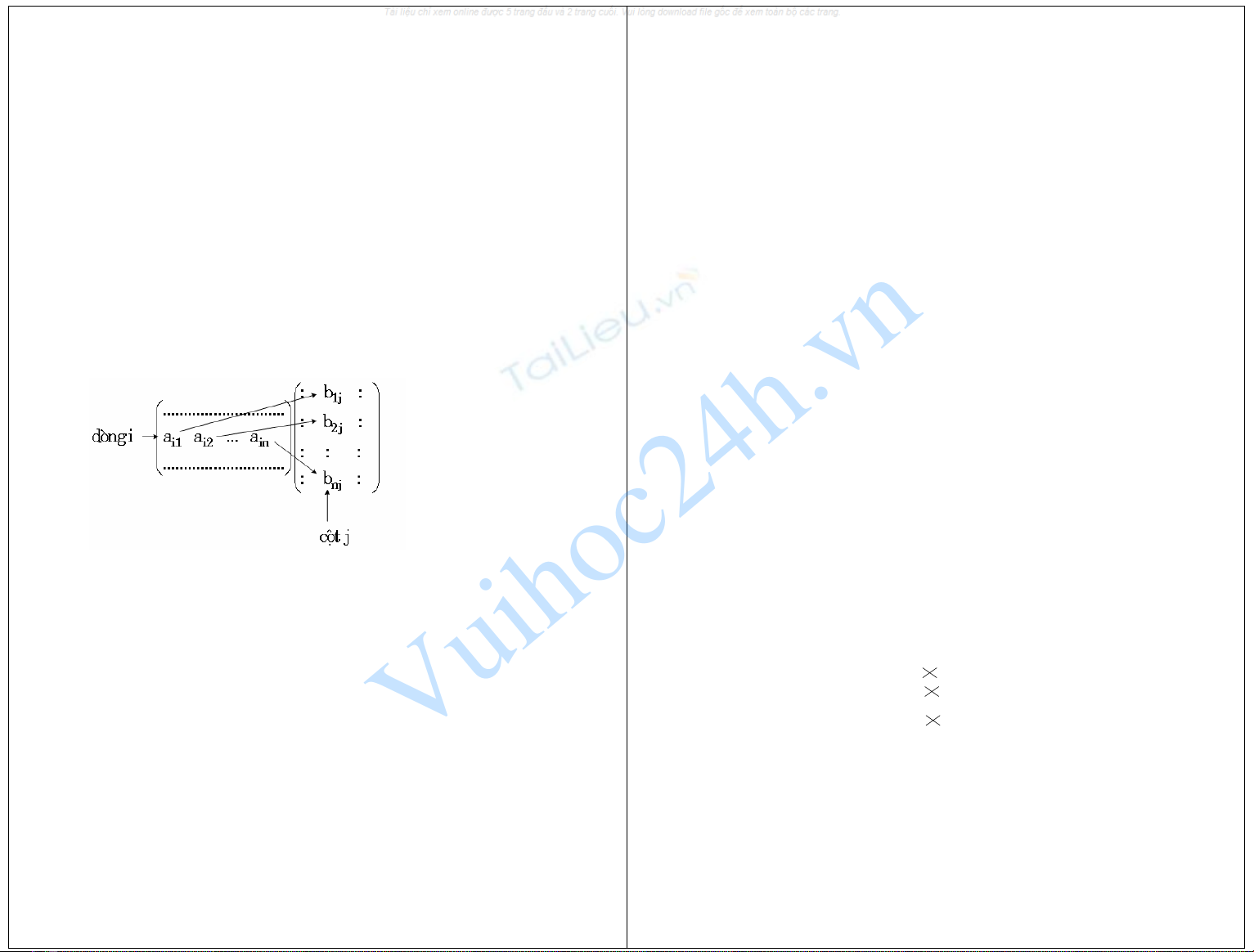
• Veà heä soá: C coù heä soá doøng i, coät j ñöôïc tính bôûi coâng thöùc:
n
ij ik kj
k1
cab
=
=∑
Noùi caùch khaùc, heä soá ôû doøng i, coät j cuûa AB coù ñöôïc baèng caùch nhaân caùc heä soá ôû
doøng i cuûa ma traän A vôùi caùc heä soá töông öùng ôû coät j cuûa ma traän B roài laáy toång
cuûa chuùng:
Ví duï: Vôùi ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
=213
121
A,
1 3
B2 1
31
⎛⎞
⎜⎟
=⎜⎟
⎜⎟
−
⎝⎠
, C = ⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛−
01
12 ta coù:
26
AB 11 8
⎛⎞
=⎜⎟
⎝⎠
;
10 5 5
BA 5 5 0
05 5
⎛⎞
⎜⎟
=⎜⎟
⎜⎟
−
⎝⎠
;
51
BC 5 2
53
−
⎛⎞
⎜⎟
=−
⎜⎟
⎜⎟
−
⎝⎠
;13 4
CA 12 1
−−
⎛⎞
=⎜⎟
−
⎝⎠
nhöng AC vaø CB khoâng xaùc ñònh.
Pheùp nhaân ma traän coù caùc tính chaát sau:
(i) Vôùi A laø ma traän loaïi m×n, ta coù:
ImA = A vaø AIn = A
Suy ra vôùi A laø ma traän vuoâng caáp n, ta coù
6
InA = A.In = A
(ii) Vôùi A laø ma traän loaïi m×n ta coù:
0p×mA = 0p×n vaø A0n×q = 0m×q
Suy ra vôùi A laø ma traän vuoâng caáp n, ta coù:
0n×nA = A.0n×n = 0n×n
(iii) Pheùp nhaân ma traän coù tính keát hôïp:
A ∈ Mm×n (R); B ∈ Mn×p (R); C ∈ Mp×q (R)
(AB)C = A(BC)
nhöng khoâng coù tính giao hoaùn, nghóa laø thoâng thöôøng AB ≠ BA (coù theå AB xaùc
ñònh nhöng BA laïi khoâng xaùc ñònh).
(iv) Pheùp nhaân ma traän coù tính phaân phoái ñoái vôùi pheùp coäng.
A(B + C) = AB + AC;
(B + C) A = BA + CA
(v) (AB)T = BTAT
(vi) Vôùi A =
11
22
2n
a
0
a
0
a
⎛⎞
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
laø moät ma traän cheùo vaø k nguyeân döông, ta coù:
k
11
kk
22
k
k
nn
a
0
A A ...A a
0
a
⎛⎞
⎜⎟
⎜⎟
⎜⎟
==
⎜⎟
⎜⎟
⎜⎟
⎜⎟
⎝⎠
Chuù yù: Nhieàu tính chaát quen thuoäc cuûa pheùp nhaân giöõa caùc soá thöïc khoâng
coøn ñuùng ñoái vôùi pheùp nhaân ma traän, chaúng haïn:
2
A 0 A = 0.
AB 0 A = 0 hay B = 0.
AB = AC B = C.
A0
=⇒
=⇒
⎧⇒
⎨≠
⎩
Ví duï: Vôùi 01 01 00
A;B;CO
00 00 00
⎛⎞⎛⎞ ⎛⎞
====
⎜⎟⎜⎟ ⎜⎟
⎝⎠⎝⎠ ⎝⎠
, ta coù A2 = 0; AB = 0; AB =
AC, nhöng A, B ñeàu khaùc 0 vaø B ≠ C.
Printed with FinePrint trial version - purchase at www.fineprint.com
Vuihoc24h.vn
7
§3. PHEÙP BIEÁN ÑOÅI SÔ CAÁP TREÂN DOØNG
3.1. Ñònh nghóa:
Cho A = (aij)m×n. Ta goïi pheùp bieán ñoåi sô caáp treân doøng (vieát taét laø BÑSCTD)
treân A laø moät trong ba loaïi bieán ñoåi sau:
1) Loaïi 1: Ñoûi hai doøng cho nhau.
Kyù hieäu : di ↔ dk chæ pheùp ñoåi hai doøng i vaø k cho nhau .
2) Loaïi 2: Nhaân moät doøng cho moät soá khaùc 0.
Kyù hieäu: di : = αdi chæ pheùp nhaân doøng thöù i cho soá α ≠ 0.
3) Loaïi 3: Coäng vaøo moät doøng moät boäi cuûa doøng khaùc.
Kyù hieäu: di : = di + βdk chæ pheùp coäng vaøo doøng thöù i boäi β (β ∈ R) laàn
cuûa doøng k ≠ i.
3.2. Ñònh nghóa:
Cho A vaø B laø hai ma traän cuøng loaïi. Ta noùi A töông ñöông doøng vôùi B, kyù
hieäu A ~ B, neáu B coù ñöôïc töø A qua höõu haïn (tuøy yù) pheùp bieán ñoåi sô caáp treân
doøng naøo ñoù.
Vaäy:
A ~ B ⇔ ∃e1, e2, ..., ek: caùc pheùp BÑSCTD sao cho
12 k
ee e
12 k
AA A...AB
⎯
⎯⎯→⎯⎯⎯→⎯⎯⎯→⎯⎯⎯→=
Nhaän xeùt: Ta thaáy quan heä töông ñöông doøng laø moät quan heä töông ñöông,
nghóa laø caùc tính chaát sau ñöôïc nghieäm ñuùng:
(i) A ~ A;
(ii) A ~ B ⇒ B ~ A
(iii) A ~ B vaø B ~ C ⇒ A ~ C
3.3. Ñònh nghóa: (Ma traän daïng baäc thang vaø daïng baäc thang ruùt goïn)
Cho A = (aij) laø moät ma traän loaïi m×n treân R. Ta noùi:
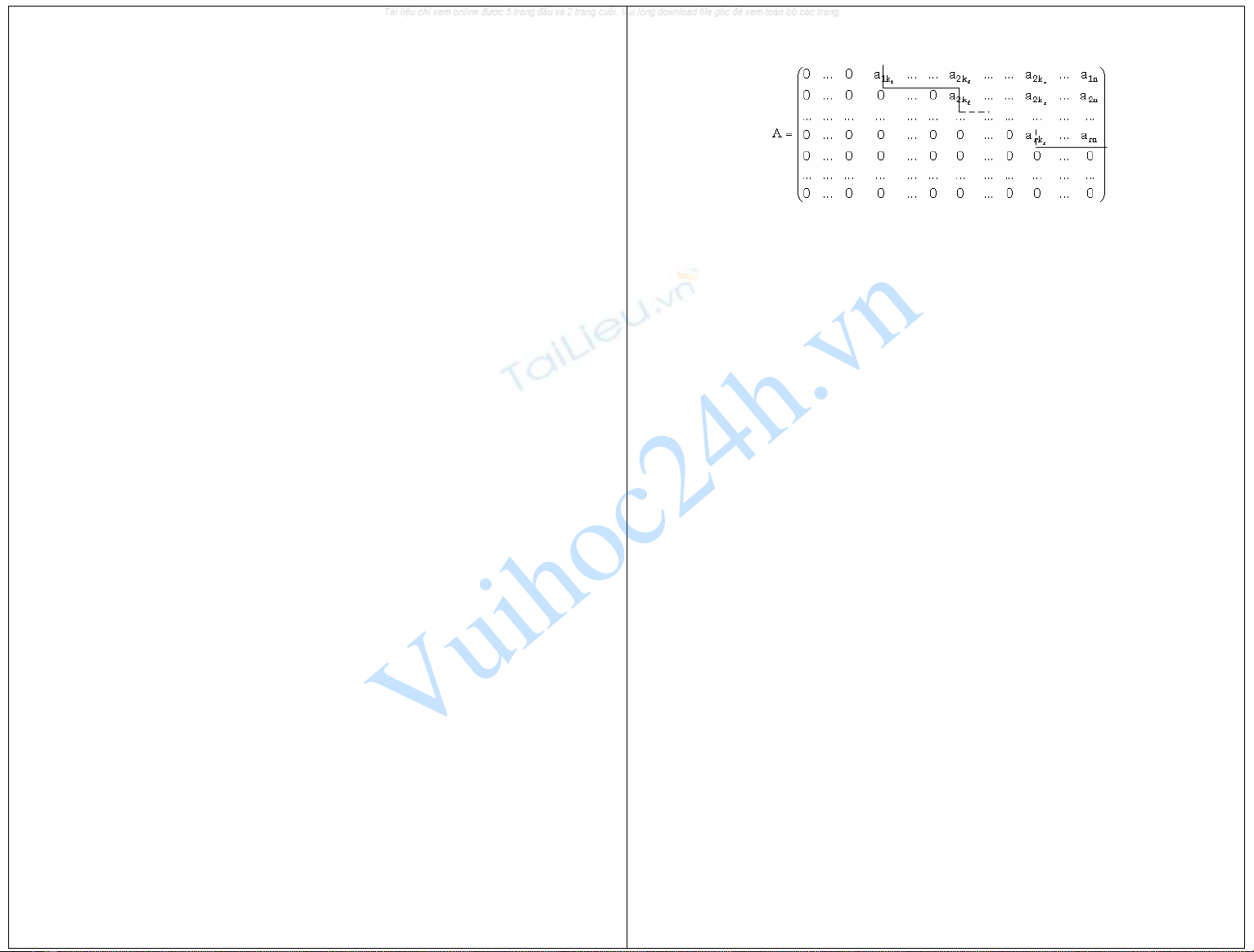
(i) A coù daïng baäc thang neáu A coù daïng sau:
8
trong ñoù k1 < k2 <...< kr vaø 12 r
1k 2k rk
a ,a ,...,a 0≠, nghóa laø A thoûa hai tính chaát
sau:
1) Caùc doøng khaùc 0 luoân luoân ôû treân caùc doøng baèng 0 cuûa A.
2) Treân hai doøng khaùc 0 cuûa A, heä soá khaùc 0 ñaàu tieân cuûa doøng döôùi bao giôø
cuõng ôû beân phaûi coät chöùa heä soá khaùc 0 ñaàu tieân cuûa doøng treân.
(ii) A coù daïng baäc thang ruùt goïn (hay coù daïng ruùt goïn theo doøng töøng baäc) neáu
tính chaát sau ñöôïc thoûa:
1) A coù daïng baäc thang.
2) Caùc heä soá khaùc 0 ñaàu tieân treân caùc doøng khaùc 0 cuûa R ñeàu baèng 1.
3) Treân caùc coät coù chöùa caùc soá 1 laø caùc heä soá khaùc khoâng ñaàu tieân treân caùc
doøng khaùc 0, taát caû caùc heä soá khaùc ñeàu baèng 0. Nghóa laø R coù daïng nhö trong (i)
vaø 12 r
1k 2k rk
aa...a1
=
== =, hôn nöõa, ngoïai tröø caùc heä soá 1 naøy, treân caùc coät k1,
k2,.., kr taát caû caùc heä soá coøn laïi ñeàu baèng 0.
Ví duï: Xeùt caùc ma traän:
12 542
00 31 7
A0000 4
00 0 0
⎛⎞
⎜⎟
⎜⎟
=⎜⎟
⎜⎟
⎝⎠
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
0000
3010
2400
1232
B
101000
01 3 00
C00 0 12
00 0 00
⎛⎞
⎜⎟
⎜⎟
=⎜⎟
⎜⎟
⎝⎠
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
00000
00100
00010
72031
D
Ta thaáy:
• A coù daïng baäc thang nhöng B khoâng coù daïng baäc thang.
• C coù daïng baäc thang ruùt goïn nhöng D khoâng coù daïng baäc thang ruùt goïn
(D chæ coù daïng baäc thang).
Printed with FinePrint trial version - purchase at www.fineprint.com
Vuihoc24h.vn

9
3.4. Ñònh lyù:
Cho A laø moät ma traän loaïi m×n treân R. Khi ñoù toàn taïi duy nhaát moät ma
traän baäc thang ruùt goïn R sao cho A ~ R. Ta goïi R laø ma traän daïng baäc thang ruùt
goïn cuûa A vaø soá löôïng doøng khaùc 0 cuûa R laø haïng cuûa ma traän A, kyù hieäu r(A).
Nhaän xeùt: Haïng cuûa ma traän A cuõng baèng soá löôïng doøng khaùc 0 cuûa baát kyø
ma traän daïng baäc thang naøo (khoâng nhaát thieát ruùt goïn) töông ñöông doøng vôùi A.
Ví du 1: Tìm moät ma traän daïng baäc thang R töông ñöông doøng vôùi ma traän:
17 1 3 0
17 1 2 2
A214 2 7 0
642 3 13 3
⎛⎞
⎜⎟
−−−
⎜⎟
=⎜⎟
⎜⎟
−
⎝⎠
Töø ñoù xaùc ñònh haïng cuûa A.
Ñaùp soá:
17 1 3 0
00 2 5 2
AR 00 0 1 0
00 0 0 0
⎛⎞
⎜⎟
−−−
⎜⎟
=⎜⎟
⎜⎟
⎝⎠
∼. Ma traän A coù haïng laø r(A) = 3.
Ví du 2: Tìm ma traän daïng baäc thang R töông ñöông doøng vôùi ma traän:
17 1 3 0
17 1 2 2
A214 2 7 0
642 3 13 3
⎛⎞
⎜⎟
−−−
⎜⎟
=⎜⎟
⎜⎟
−
⎝⎠
Ñaùp soá:
1700 1
0010 1
AR 0001 0
0000 0
−
⎛⎞
⎜⎟
⎜⎟
=⎜⎟
⎜⎟
⎝⎠
∼.
§4. MA TRAÄN KHAÛ NGHÒCH
4.1. Ñònh nghóa:
Moät ma traän A vuoâng caáp n ñöôïc goïi laø khaû nghòch neáu coù moät ma traän B
vuoâng caáp n sao cho AB = BA = In. Khi ñoù ma traän B laø duy nhaát vaø ñöôïc goïi laø
ma traän nghòch ñaûo cuûa A kyù hieäu laø A–1.
Nhaän xeùt:
10
1) Neáu ma traän A coù moät doøng hay moät coät baèng 0 thì A khoâng khaû nghòch.
Ñaûo laïi khoâng ñuùng.
2) Ma traän ñôn vò I khaû nghòch vaø I–1 = I.
3) Vôùi A, B laø hai ma traän vuoâng caáp n ta coù:
(A khaû nghòch vaø A-1 = B) ⇔ AB = In ⇔ BA = In
4) Neáu A khaû nghòch vaø α ∈ R, α ≠ 0 thì ma traän αA cuõng khaû nghòch vaø
11
1
(A) A
−−
α=
α.
5) Neáu A khaû nghòch thì AT cuõng khaû nghòch vaø
(AT)–1 = (A–1)T
6) Neáu A, B laø hai ma traän khaû nghòch coù cuøng caáp thì ma traän tích AB
cuõng khaû nghòch vaø:
(AB)–1 = B-1A–1
4.2. Ñònh lyù:
Cho A laø moät ma traän vuoâng caáp n. Ta coù caùc khaúng ñònh sau töông ñöông:
1) A khaû nghòch.
2) r(A) = n.
3) A ~ In .
4) Toàn taïi caùc pheùp BÑSCTD e1, e2, ..., ek bieán ma traän A thaønh ma traän ñôn
vò In.
Hôn nöõa, khi ñoù cuõng qua chính caùc pheùp bieán ñoåi e1, e2,..., ek, ma traän ñôn
vò In seõ bieán thaønh ma traän nghòch ñaûo A–1, nghóa laø:
Neáu 3
12 k
e
ee e
12 kn
AA A ...AI
⎯
⎯⎯→⎯⎯⎯→⎯⎯⎯→⎯⎯⎯→=
thì 312 k
e
ee e 1
n12 k
IBB...BA
−
⎯⎯⎯→⎯⎯⎯→⎯⎯⎯→⎯⎯⎯→= .
Chuù yù: Trong thöïc haønh, ñeå xeùt tính khaû nghòch cuûa ma traän A vuoâng caáp n
vaø tìm A-1 (neáu coù), ta tieán haønh nhö sau: Xeáp In beân phaûi ma traän A: (A⏐In) vaø
duøng caùc pheùp BÑSCTD ñeå bieán ñoåi ma traän naøy theo höôùng ñöa A veà daïng baäc
thang ruùt goïn R:
Printed with FinePrint trial version - purchase at www.fineprint.com
Vuihoc24h.vn























![Đề thi cuối kì môn Mô hình hóa toán học [kèm đáp án]](https://cdn.tailieu.vn/images/document/thumbnail/2026/20260121/lionelmessi01/135x160/83011768986868.jpg)


