www.laisac.page.tl
CHUYÊNĐỀ
P
P
PH
H
HƯ
Ư
ƯƠ
Ơ
ƠN
N
NG
G
GT
T
TR
R
RÌ
Ì
ÌN
N
NH
H
HV
V
VÀ
À
ÀB
B
BẤ
Ấ
ẤT
T
TP
P
PH
H
HƯ
Ư
ƯƠ
Ơ
ƠN
N
NG
G
GT
T
TR
R
RÌ
Ì
ÌN
N
NH
H
H
Q
Q
QU
U
UI
I
IV
V
VỀ
Ề
ỀB
B
BẬ
Ậ
ẬC
C
CH
H
HA
A
AI
I
I
A).PHƯƠNGTRÌNHVÀBẤTPHƯƠNGTRÌNHCHỨACĂNTHỨC
I.DẠNGCƠBẢN
Chúý:ĐểtồntạiAthì 0 ³A; 0 ³A
Khigiảilưuýbabướcsau:
1.Biểuthứcngoàicăn.
2.Biểuthứctrongcăn.
3.Làmmấtcănđểgiải
1).DạngPhươngtrình cơbản
3
3
2
0
)0(0
BABA
BA
B
BA
BA
BhayA
BA
= Û = ·
î
í
ì
=
³
Û = ·
î
í
ì
=
³ ³
Û = ·
2.DạngBấtphươngtrìnhcóbảncơbản
2
A 0
A B B 0
A B
ì ³
ï
< Û >
í
ï <
î 2
A 0
B 0
A B B 0
A B
é ³
ì
í
ê <
î
ê
> Û ê ³
ì
ï
ê
í
ê >
ï
î
ë
II).MỘTSỐVÍDỤ:
Giảiphươngtrình
Bài1.2
4 2 2x x x + - = -
2 2 2
2 0 2
4 2 ( 2) 3 0
2 3
0 3
x x
x x x x x
x x
x x
- ³ ³
ì ì
Û Û
í í
+ - = - - =
î î
³
ì
Û Û =
í = Ú =
î
Bài2. 4 1 1 2x x x + - - = -
1 1
4 4
2 2
4 1 2 (1 )(1 2 ) 1 2 (1 )(1 2 ) 2 1
x x
x x x x x x x x
ì ì
- £ £ - £ £
ï ï
Û Û
í í
ï ï
+ = - + - - + - - - = +
î î
2
1
4 1 1
2
1 2 2 0
7
2 0
(1 )(1 2 ) 4 4 1 2
x
x
x x
x x
x x x x
ì
- £ £
ï ì
ï - £ £
ï
ï ï
Û ³ - Û Û =
í í
ï ï = Ú = -
ï
ï - - = + + î
ï
î
Bài3.Giảicácbấtphươngtrìnhsauđây
1) 1)1(2 2 + £ - xx( 311 £ £ Ú - = xx)
2) 02162 2 > + - + - xxx( 3 1 7; 3
2 2
x x £ - >)
3) 3x +– 1x -< 2x -( 2 21
3
x>)
BÀITẬP:
Giảicácphươngtrìnhvàbấtphươngtrìnhsau:
Bài1:Giảicácphươngtrình
2
2
1
1) 3 9 1 2 0 : 2
11
2) 2 9 4 3 1 : ; 0
3
3) 5 1 3 2 1 0 : 2
4) 2 3 5 2 4 6 0 : 2
x x x DS x
x x x DS x x
x x x DS x
x x x x DS x
-
- + + - = =
+ = - + + = =
- - - - - = =
- + - - + - = =
Bài2:Giảicácbấtphươngtrình
7
1) ( 1)(4 ) 2 ( 1 ; )
2
x x x x x + - > - - £ <
2) 7 1 3 18 2 7 ( 9)x x x x + - - £ + ³
3) 5 1 1 2 4 ( 10 2)x x x x x - - - > - < Ú ³
4)
2
51 2 1 ( 5; 1 2 13; 1; 1 2 13)
1
x x x x x x
x
- - < < - ³ - - > £ - +
-
5)
2
1 1 4 2 1 1
3 ( ; ;0 )
4 2 2
x x x x
x
- - < < - ³ - < £
II.PHƯƠNGPHÁPĐẶTẨNSỐPHỤ:
Cácdạngđặtẩnphụthườnggặpsauđây
Dạng2 2
ax axbx m bx c n + + + + =
Đặt 2
axt bx c = + +kèmtheođiềukiện
VíDụ 1:Giảiphươngtrình
–4 )2)(4( x x + -= 2
x–2x–8(1)
HD:Đặtt= )2)(4( x x + -(t³0)
(1)trởthành:– 4t=– 2
t Û ê
ë
é
=
=
4t
0t
Vídụ2:Giảibấtphươngtrình
1) (x+5)(2–x) ³=3 x3x2 +.
2) 2855)4)(1( 2 + + < + + xxxx(– 9<x<4)
Dạng
( )( )
ncxbcxadcxbcxa = - + + - + +
Phươngpháp.Đặtt=cxbcxa - + +;ĐK: )(2 batba + £ £ +.
HD:Đặt 3 6t x x = + + -.Đưavềphươngtrình:t
2 –2t–3=0
Vídụ 1.Chophươngtrình:mxxxx = - + - - + + )3)(1(31
a) Giảip/tkhim=2. ĐS:x=1hoặcx=3.
b) Tìmm đểp/tcónghiệm. Đs 2222 £ £ - m
Vídụ 2:Giảiphươngtrình
1x ++ x4 -+ )x4)(1x( - +=5(1)
HD: Đặtt= 1x ++ x4 - Þ)x4)(1x( - += 2
5t2 -
(1)trởthành:t+ 2
5t2 -=5.
Vídụ 3 Giảibấtphươngtrình
2
3 2 1 4 9 2 3 5 2x x x x x - + - ³ - + - +
Vídụ 4:Giảiphươngtrìnhsauđây: . 2 5 3 2 9 4 1 2 3 2 + - + - = - + - x x x x x
Dạng: .
''
).()'')(.( m
bax
bxa
baxbxabax =
+
+
+ + + +
b a
Phươngpháp :Đặt =t)'')((
''
)( 2bxabaxt
bax
bxa
bax + + = Þ
+
+
+.
Phươngtrìnhđãchotrởthành: 0
2 = - + mtt
b a
.
Vídụ:Chophươngtrình: .
3
1
)3(4)1)(3( m
x
x
xxx =
-
+
- + + -
1. Giảiphươngtrìnhkhim=3.
2. Địnhthamsốmđểphươngtrìnhcónghiệm.
HD:Đặt 2
1
( 3) ( 3)( 1)
3
x
t x X x x
x
+
= - Þ = - +
-nênpt(1)đưavề:t
2
+4tm=0(2)
a) Vớim=3thìphươngtrình(2)trởthành 2 1
4 3 0 3
t
t t t
= -
é
+ + = Û ê = -
ë
Đs 1 5x = -, 1 13x = -
b)Trướchếtphươngtrình(2)cónghiệm 0 4 0 4m m
¢
Û D ³ Û + ³ Û ³ -.
Giảsửnghiệmlàt0 thì 0
1
( 3) 3
x
x t
x
+
- =
-.
+Nếut0 =0thìx=–1
+Nếut0 >0thì 2
0
2
0
3 1 4
( 3)( 1)
x x X
x x t
>
ì Û = + +
í - + =
î
+Nếut0<0thì 2
0
2
0
3 1 4
( 3)( 1)
x x t
x x t
<
ì Û = - +
í - + =
î
Vậyvới 4m ³ -thìphươngtrình(2)cónghiệmtứclàphươngtrình(1)cónghiệm.
Dạng: ) 1 ( .
2 ¹ = ± + a a x a x.
Phươngpháp :Đặt ).0( ³ = + ttaxĐưaphươngtrìnhvềhệ ï
î
ï
í
ì
= -
= +
axt
atx
2
2
Trừhaivếtheovếtađưavềdạng(t+x)(x–t+1)=0.
Vídụ: Giảiphươngtrình: . 2007 2007
2 4 = + + x x
HD.Đặtt
2 = 2007
2 + x.Phươngtrìnhtrởthành 0 ) 1 )( (
2007
2007 2 2 2 2
2 4
2 4
= - - + Þ
ï
î
ï
í
ì
= -
= + t x t x
x t
t x.
Chúý:Cóthểgiảicáchkhácnhưsau:
Phươngtrình 4
1
2007 2007
4
1 2 2 2 4 + + - + = + + Û x x x x
2
2
2
2
2
1
2007
2
1 ÷
ø
ö
ç
è
æ - + =
÷
ø
ö
ç
è
æ + Û x x.
Dạng: ) ( . N n b ax a b x n
n Î - = +.
Phươngpháp :Đặtn baxt - =,tacóhệ ï
î
ï
í
ì
= +
= +
axbt
atbx
n
n
Vídụ 1:Giảiphươngtrìnhsau: 3
3 1221 - = + xx; 3
3 2552 - = + xx
HD.Đặt ï
î
ï
í
ì
= +
= +
Þ - =xt
tx
xt21
21
12 3
3
3
Vídụ 2:Giảiphươngtrình 3 3
1 2 2 1x x + = -.
Hướngdẫn:Đặt
3
3
3
3
1 2
2 1 1 2 1 2
x y
y x y x y x
ì + =
ï
= - Û + = Þ í + =
ï
î
.Đápsố:x=1; 1 5
2
x - ±
=
ĐUAVỀHỆPHƯƠNGTRÌNH
Vídụ1.Giảiphươngtrình: 3 10 25 2 2 = - - - x x.
HD.TXĐ: 1010 £ £ - x.
Đặt 2
25 x -=avà 2
10 x -=b(a,b ³0)
Việcgiảiphươngtrình,chuyểnvềgiảihệPThữutỉsau: î
í
ì
= -
= -
15
3
22ba
ba
Vídụ 2.Giảiphươngtrình: 211 33 = - + + xx
HD.TXĐ:x ³0. Đặt3 1 x +=avà 3 1 x -=b.
ViệcgiảiPT(3)chuyểnvềgiảihệPT î
í
ì
= +
= +
2
2
33ba
ba
Giảihệphươngtrìnhnàyđượca=b=1.Từdósuyrax=0 Ûx=0.
Vídụ3.Giảiphươngtrình 3 7x +– x =1(1)
HD+Cách1:Đặtt= x (t ³0)
(1)trởthành3 2 7t +=t+1 Û2
t +7= 3
t +3 2
t +3t+1
Û(t–1)( 2
t +3t+6)=0(Bạnđọctựgiải)(ĐSx=1)
+Cách2:Đặt ï
î
ï
í
ì
=
+ =
xv
7xu 3
cóhệ î
í
ì
= -
= -
7vu
1vu
23
Vídụ 4.Giảiphươngtrình
3x +–3 x =1(1)
HD+Cách1:Đặtt=3 x,(1)trởthành: 1t
3 +=t+1
+Cách2:Đặt ï
î
ï
í
ì
=
+ =
3 xv
3xu cóhệ î
í
ì
= -
= -
3vu
1vu
32 (ĐS 1; 2 2)x x = =
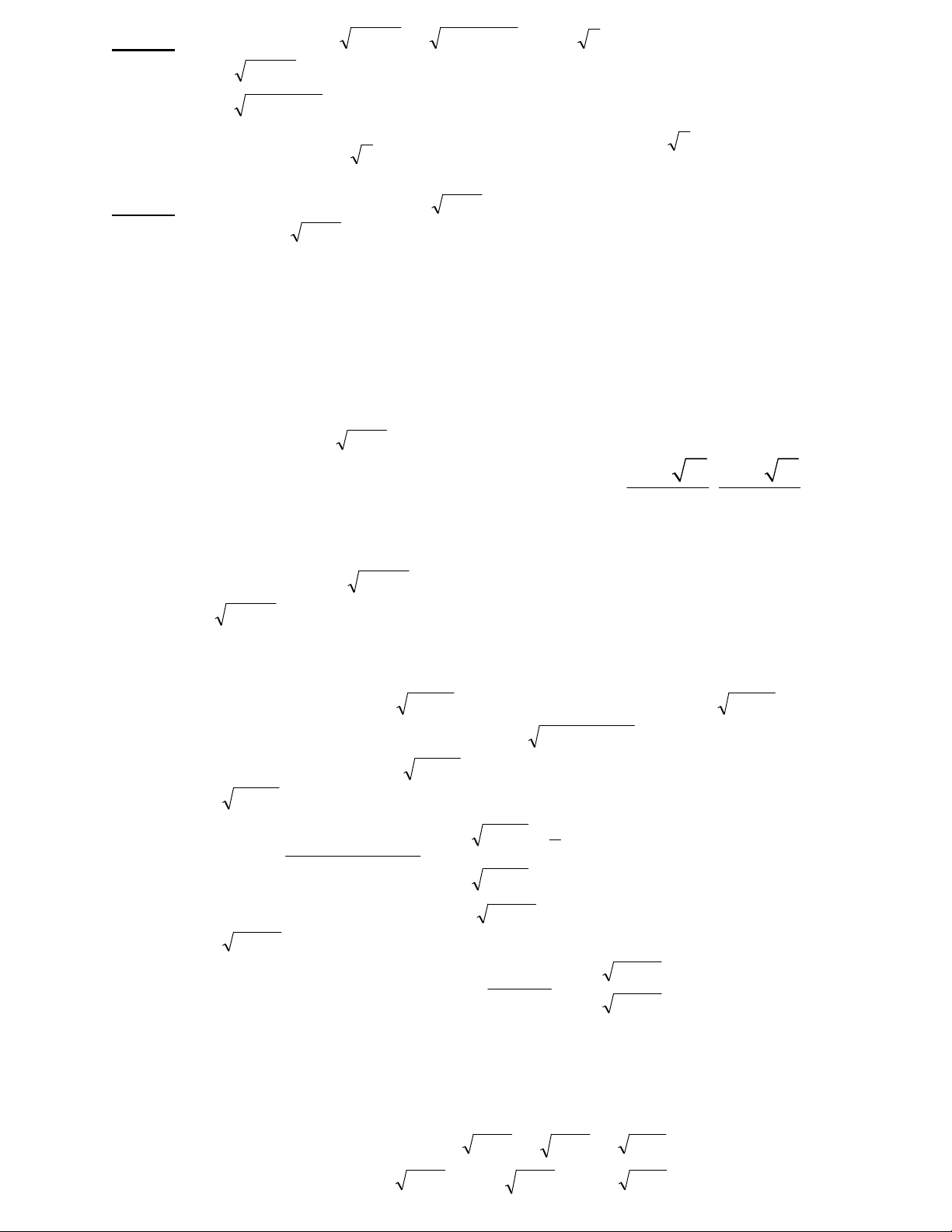
Vídụ 5:Giảiphươngtrình xx2 ++ 7xx2 + +=3+ 2 (1)
Giải Đặt ï
î
ï
í
ì
+ + =
+ =
7xxv
xxu
2
2
(1)trởthành:u+v=3+ 2.Tacóhệphươngtrình ï
î
ï
í
ì
= -
+ = +
7uv
23vu
22
Vídụ 6: Giảiphươngtrình 2
x +4x= 6x +(1)
HD · Tadựkiếnđặt 6x +=at+bđểđưavềhệphươngtrìnhđốixứng:
Tacóhệphươngtrình: ï
î
ï
í
ì
- + = +
+ = +
222
2
b6xabt2ta
batx4x
hệnàyđốixứngnếu
ï
ï
î
ï
ï
í
ì
- =
=
=
=
2
2
b6b
1a
4ab2
1a
Û î
í
ì
=
=
2b
1a
.Nhưvậytađặtt+2= 6x +(t ³–2)
Khiđócóhệptđốixứng: ï
î
ï
í
ì
+ = +
+ = +
2xt4t
2tx4x
2
2
(ĐS 3 17 5 13
; )
2 2
x - - - +
=
+ĐẶTẲNMỚI,ẨNCŨCÒNLẠIXEMNHƯTHAMSỐ.
Vídụ1:Giảiphươngtrình:
( )
23132 22 + - = - + xxxx.
HD:Đặt 2
2 + = xt.PTtrởthành:
( ) ( )
01213
2 = - + - - xxtxt
Giảiphươngtrinhbậc2ẩnt,tacó: ê
ë
é
- =
=
12xt
xt
Vídụ2:Giảiphươngtrình:
( )
( )
1212114 22 - + + = + - xxxx(HD:Đặt 1
2 + = xt.)
Thídụ3:Giảiphươngtrình: . 0 5 6 6 ) 1 4 ( 5 10 6 2 2 = + - - - + - x x x x x
Vídụ 4:Giảiphươngtrình(4x–1) 1x2 +=2 2
x +2x+1(1)
HD:Đặtt= 1x2 +(t ³1)(1)trởthành(4x– 1)t=2 2
t +2x–1
D= 2
)3x4( - Þt= 4
)3x4()1x4( - ± - Û
ê
ê
ê
ë
é
- = +
= +
1x21x
2
1
1x
2
2
Vídụ 5:Giảiphươngtrình2 2
x –3x+2=x 2x3 -(1)
HD:Đặtt= 2x3 -(t ³0)(1)trởthành 2
t +xt–2 2
x =0.
·Cách1: D=9 2
x (chínhphương) Þt= 2
x3x ± - Û ê
ê
ë
é
- = -
= -
x22x3
x2x3
·Cách2:phươngtrìnhđẳngcấp Þđặtx=ty:
2
t +y 2
t –2 2
y 2
t =0 Û2
t (1+y–2 2
y )=0.
*ĐƯAVỀTỔNGBÌNHPHƯƠNG: î
í
ì
=
=
Û = + 0
0
0
2 2
B
A
B A
Vídụ1.Giảiphươngtrình.5634224 - + - + - = + + + zyxzyx
HD:Phươngtrìnhtươngđương
( ) ( ) ( )
0352312 222 = - - + - - + - - zyx.