Kinh tế lượng ứng dụng - Bài tập 1

Chia sẻ: Meomeo Ten | Ngày: | Loại File: DOC | Số trang:13

Thêm vào BST

Báo xấu

115
lượt xem 16
download

Download Vui lòng tải xuống để xem tài liệu đầy đủ

Các quan hệ đồng biến, hay tổng thu nhập cá nhân tăng thì tổng chi tiêu dành cho chăm sóc sức khỏe tăng.. Hãy cho biết có mối tương quan tuyến tính giữa tổng chi tiêu dùng cho chăm sóc sức khỏe

Chủ đề:

Bình luận(0) Đăng nhập để gửi bình luận!

Lưu

Nội dung Text: Kinh tế lượng ứng dụng - Bài tập 1

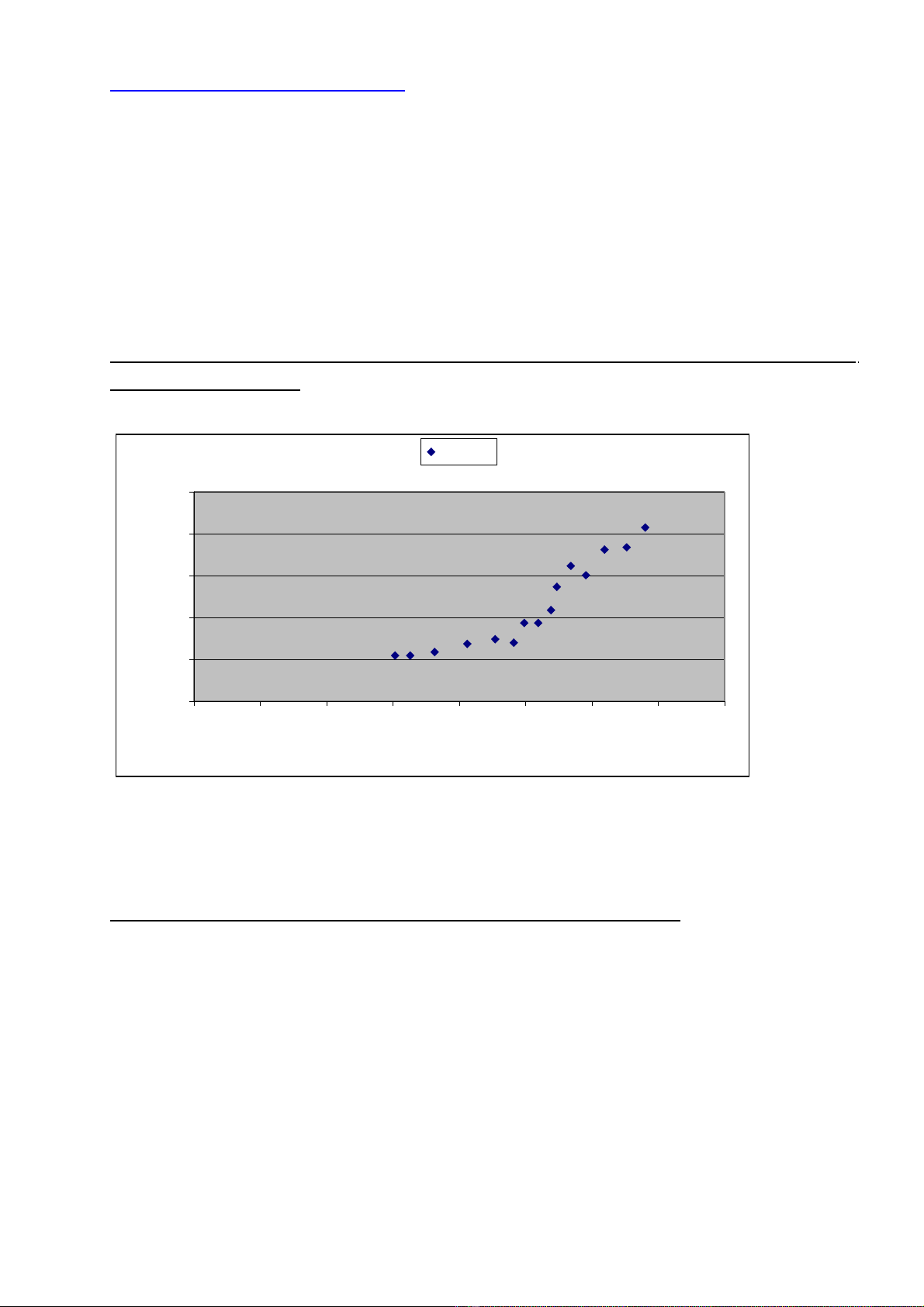
http://www.facebook.com/DethiNEU Nhóm 6: KINH TẾ LƯỢNG ỨNG DỤNG BÀI TẬP 1 Bài 1 (BT2-Fullright) Câu 1: (Dữ liệu AM06-PS2-sheet 1) EXPHLTH: Tổng chi tiêu dành cho chăm sóc sức khỏe (tỷ USD) INCOME: Tổng thu nhập cá nhân (tỷ USD) 1a. Vẽ đồ thị phân tán (Scatter Diagram) cho tập dư liệu trên. Dùng tr ục hòanh cho bi ến INCOME và trục tung chobiến EXPHLTH. Dựa vào dữ liệu AM06-PS2- sheet 1, ta có Đồ thị phân tán sau: BT2, Ca u1a . DO THI P HAN TAN 800 600 EXP HLTH 400 200 0 0 20 40 60 80 100 INCOME 1b. Tính các trị thống kê tổng hợp cho biến lương biến INCOME VÀ EXPHLTH. Đặt EXPHLTH là Y và INCOME là X, ta có: Trung bình: Y = ∑Y / n = 768.512 / 51 = 15.068863 X = ∑X/ n = 5361.8 / 51 = 105.1333 Phương sai: SY2= ∑(Yi - Y )2 / (n-1) = 16068.214 / 50 = 321.3643 SX2= ∑(Xi - X )2 / (n-1) = 784951.293 / 50 = 15699.026 Độ lệch chuẩn: SDY = √?SY2 = 321.3643 = 17.92663622 SDX = √?SX2 = 15699.026 = 125.296 -1-
http://www.facebook.com/DethiNEU Đồng phương sai Cov (X,Y) = (1/n-1) * ∑(Xi - X ) . (Yi - Y ) ⇒ Cov (X,Y) = (1/ 51-1) * 111190.066 = 2223.801 1c. Dùng CORREL trong Excel, xác định hệ số tương quan tuyến tính (r) gi ữa t ổng chi tiêu dùng cho chăm sóc sức khỏe EXPHLTH và tổng thu nhập cá nhân INCOME. Ta tính đựơc r= 0.990058425 Hoặc tính theo: ˆ β = ∑XiYi – n( X * Y ) / ∑Xi2 – n ( X )2 = ˆ β = 191986.2936 – 51(105.1333)(15.06886) / 1348655.2 – 51(105.1333)2 ˆ β = 0.141652 ˆ α = Y - β * X = 15.068863 – (0.141652 * 105.1333) = 0.176496 ˆ TSS= ∑Yi2 – n *( Y )2 = 27648.816 – 51*(15.069)2 = 16068.214 ˆ ˆ ESS = β 2*∑xi2 = β 2*∑(Xi- X )2 = (0.141652)2 * (784951.293) = 15750.275 RSS= TSS- ESS = 16068.214 - 15750.275 = 317.940 Hệ số xác định R2 = ESS/ TSS = 15750.275 / 16068.214 = 0.9802132 Hệ số tương quan: r= ±√?R2 = ±√?0.9802132 = ± 0.9900584 Ý nghĩa: ˆ a) r và β có cùng dấu , do đó r=0.9900584 ˆ b) β >0 và r >0, nên X và Y có quan hệ đồng biến, hay tổng thu nh ập cá nhân tăng thì t ổng chi tiêu dành cho chăm sóc sức khỏe tăng. 1d. Hãy cho biết có mối tương quan tuyến tính giữa t ổng chi tiêu dùng cho chăm sóc s ức kh ỏe EXPHLTH và tổng thu nhập cá nhân INCOME ở mức ý nghĩa α=5% hay không. Gọi β là hệ số tương quan tuyến tính giữa tổng chi tiêu dành cho chăm sóc sức khỏe và tổng thu nhập cá nhân. Đặt giả thiết X và Y có mối tương quan tuyến tính. H0: β = 0 H1: β # 0 Tại 1c, Ta đã có r = 0.9900584 Tính t0 = r / √?[ (1-r2) / (n-2)] = 0.9900584 /√?[(1- 0.99005842)/49]= 49.2717867 Với α=5%, α/2= 0.025, tra bảng tn-2, α/2= t49,0.025= 2.010 -2-
http://www.facebook.com/DethiNEU Vì t0 > t49,0.025 nên tổng chi tiêu dùng cho chăm sóc sức khỏe EXPHLTH và tổng thu nhập cá nhân INCOME có mối tương quan tuyến tính ở mức ý nghĩa α=5%. Câu 2. (Dữ liệu AM06-PS2-sheet 2) CPI: chỉ số giá tiêu dùng NYSE: chỉ số chứng khóan trên thị trường chứng khóan New York T: thời kỳ 1977~1991. 2a. Vẽ đồ thị phân tán (Scatter Diagram) cho tập dư liệu trên. Dùng tr ục hòanh cho bi ến CPI và trục tung cho biến NYSE. 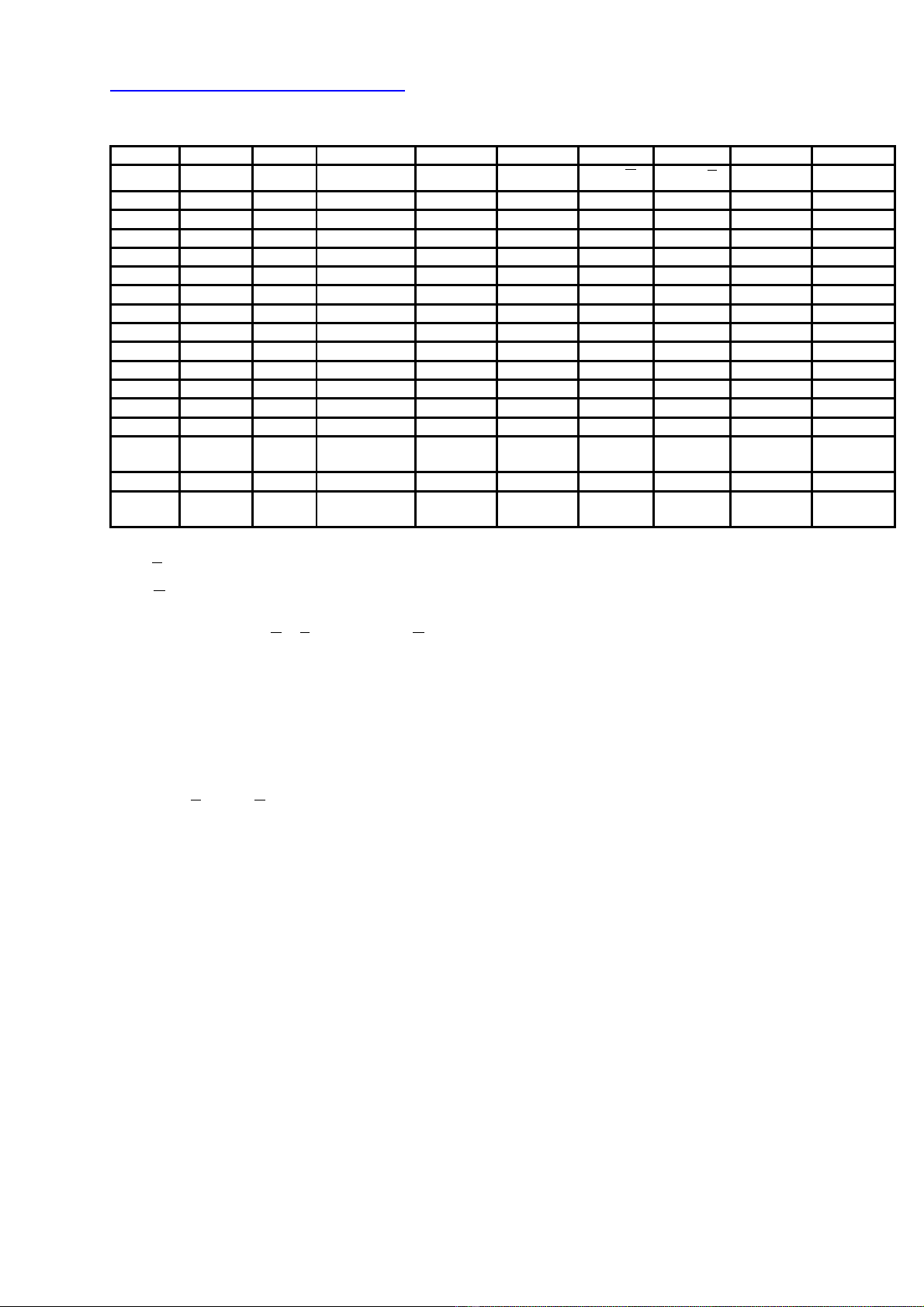Dựa vào dữ liệu AM06-PS2-sheet 2, ta có Đồ thị phân tán sau: Series1 250 200 150 NYSE 100 50 0 0 20 40 60 80 100 120 140 160 CPI Nhận xét: Bằng trực quan, nhận thấy CPI và NYSE có mối quan hệ đồng biến. Sử dụng Excel/ Graph/ Scatter XY. 2b. Anh Vũ đề nghị mô hình hồi quy tuyến tính NYSEt = α + β CPIt + ut Ước lượng các hệ số độ dốc β và tung độ gốc α của mô hình bằng 4 cách: Cách 1: Dựa trên công thức tính của phương pháp bình phương tối thiểu OLS. -3-
http://www.facebook.com/DethiNEU Năm NYSE CPI t Y X XY ˆ X 2 ˆ Y2 x=X- X y = Y- Y ˆ y2 ˆ x2 1977 53.69 60.6 3253.614 3672.36 2882.616 -40.18 -58.855 3463.872 1614.432 1978 53.7 65.2 3501.24 4251.04 2883.69 -35.58 -58.845 3462.695 1265.936 1979 58.32 72.6 4234.032 5270.76 3401.222 -28.18 -54.225 2940.314 794.112 1980 68.1 82.4 5611.44 6789.76 4637.61 -18.38 -44.445 1975.328 337.824 1981 74.02 90.9 6728.418 8262.81 5478.96 -9.88 -38.525 1484.15 97.614 1982 68.93 96.5 6651.745 9312.25 4751.345 -4.28 -43.615 1902.239 18.318 1983 92.63 99.6 9225.948 9920.16 8580.317 -1.18 -19.915 396.5939 1.392 1984 92.46 103.9 9606.594 10795.21 8548.852 3.12 -20.085 403.3938 9.734 1985 108.9 107.6 11717.64 11577.76 11859.21 6.82 -3.645 13.2836 46.512 1986 136 109.6 14905.6 12012.16 18496 8.82 23.455 550.1527 77.792 1987 161.7 113.6 18369.12 12904.96 26146.89 12.82 49.155 2416.247 164.352 1988 149.91 118.3 17734.353 13994.89 22473.01 17.52 37.365 1396.168 306.950 1989 180.02 124 22322.48 15376 32407.2 23.22 67.475 4552.921 539.168 1990 183.46 130.7 23978.222 17082.49 33657.5 29.92 70.915 5028.985 895.206 7 1991 206.33 136.2 28102.146 18550.44 42572.07 35.42 93.785 8795.689 1254.576 Tổng 1688.1 1511.7 185942.592 159773.1 228776.6 0.000 0.000 38782.03 7423.924 7 Y = ∑Y / n = 1688.17 / 15 = 112.5447 X = ∑X/ n = 1511.7 / 15 = 100.78 ˆ β = ∑XiYi – n( X * Y ) / ∑Xi2 – n ( X )2 ˆ β = [185942.6– 15(100.78)(112.5447)] / [1597731 – 15(100.78)2] ˆ β = 2.1294425 ˆ α = Y - β * X = 112.5447 – (2.1294425 * 100.78) = -102.06055 ˆ Cách 2: Dùng các lệnh SLOPE và INTERCEPT trong Excel. ˆ Excel = SLOPE (Y, X) = β = 2.1294425 Excel = INTERCEPT (Y, X) = α = -102.06055 ˆ -4-
http://www.facebook.com/DethiNEU Cách 3: Dùng công cụ DATA ANALYSIS trong Excel SUMMARY OUTPUT Bài tập 2, Câu 2b, sử dụng công cụ Data Analysis trong Excel Regression Statistics 　 Multiple R 0.931681352 R Square 0.868030141 Adjusted R Square 0.857878613 Standard Error 19.84179586 Observation 15 ANOVA 　 df SS MS F P- value Regression 1 33663.97216 33663.97216 85.50734163 4.43E-07 Residual 13 5118.059218 393.6968629 Total 14 38782.03137 　　　　 Coefficient Standard error t Statistics P- value Lower limit 95% Intercept -102.0605501 23.76678031 -4.29425226 8.73E-04 -153.4055474 X Variable 2.129442516 0.230284241 9.247017986 4.43E-07 1.631943756 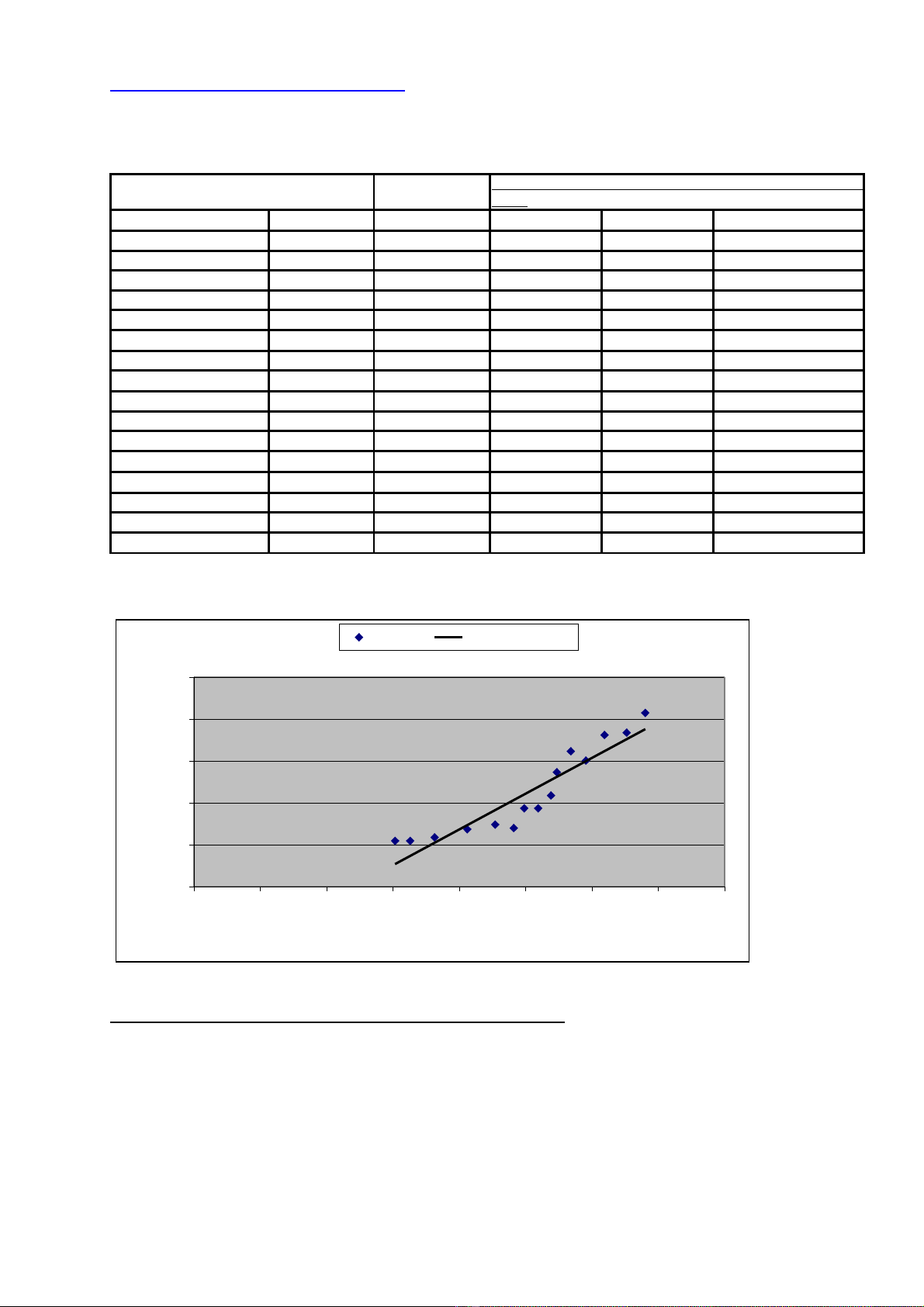Cách 4: Dùng công cụ ADD TRENDLINE trong Ecxel. Series1 Linear (Series1) 250 200 150 NYSE 100 50 0 0 20 40 60 80 100 120 140 160 CPI 2c. Viết phương trình hồi quy ước lượng của mô hình trên: NYSEt = -102.06055 + 2.1294425 CPIt + ut Ý nghĩa hệ số độ dốc: ˆ β = 2.1294425 Khi chỉ số giá tiêu dùng CPI tăng (ho ặc gi ảm 1%) thì chỉ s ố ch ứng khóan NYSE cũng tăng (ho ặc giảm) với chỉ số tương đương 2.1294425 tại thời điểm 1977~1991. Với điều kiện các yếu tố -5-
http://www.facebook.com/DethiNEU khác không đổi. 2d. Xác định mối quan hệ tuyến tính có ý nghĩa về mặt thống kê với mức ý nghĩa α=5% giữa CPI và NYSE. Đặt giả thiết, CPI(X) và NYSE(Y) không có mối quan hệ tuyến tính về mặt thống kê (X không ảnh hưởng đến Y) H0: β = 0 H1: β # 0 Tại 2b, Ta đã có p-value = 4.43E-07= 0.0443%
http://www.facebook.com/DethiNEU ut 30.000 20.000 10.000 0.000 1976 1978 1980 1982 1984 1986 1988 1990 1992 -10.000 -20.000 -30.000 -40.000 Series1 ˆ Nhận xét: Bằng trực quan, nhận thấy đại lượng sai số u t dao động quanh trục hòanh. Sử dụng Excel/Graph. Câu 3. GNP bình quân đầu người (GNPKAP) (tính theo USD) Tỉ lệ học sinh cấp hai (EDUC) Các trị thống kê. GNPKAP EDUC Number 30 30 Average 182 42.4% Std Dev(SD) 35.2 14.6% Max 259.3 67.6% Min 105 20.8% ˆ ˆ Mô hình 1: EDUCi = a + b *GNPKAPi + êi ˆ ˆ Mô hình 2: GNPKAPi = α + β * EDUCi + u i (tác động của EDUC đối với GNPKAP) ˆ Xác định hệ số độ dốc (β) và tung độ gốc (α) sử dụng trong mô hình 2. Đặt GNPKAP là Y và EDUC là X, ta có: ˆ b = cov(Y,X) / SY2 ˆ β = cov(Y,X) / SX2 ˆ với kết quả hồi quy của mô hình 1, b = 0.00344 ˆ ˆ nên b / β = Sx2 / Sy2 -7-
http://www.facebook.com/DethiNEU ˆ ˆ β =( b * Sy2) / Sx2 = (0.00344* 35.22 / 14.6% = 199.95767 ˆ α = Y - β * X = 182 – (199.95767* 42.4%) = 97.21795 ˆ ˆ Vậy mô hình 2 có hàm hồi quy GNPKAPi = 97.21795 + 199.95767 * EDUCi + u i ˆ Với α = 97.21795 và β = 199.95767 ˆ -8-
http://www.facebook.com/DethiNEU Bài 2 (BT3-Fullright) Câu 1. (Dữ liệu AM06-PS2-sheet 2) chuyển qua Eview CPI: chỉ số giá tiêu dùng NYSE: chỉ số chứng khóan trên thị trường chứng khóan New York T: thời kỳ 1977~1991. 1a. Tính các trị thống kê tổng hợp cho biến lương biến NYSE và CPI. Eview: Group Statistics / Decriptive Statistics / Common sample 　 CPI GNPKAP Mean 100.78 112.5447 Median 103.9 92.63 Maximum 136.2 206.33 Minimum 60.6 53.69 Std. Dev. 23.02782 52.63217 Skewness -0.28628 0.436896 Kurtosis 2.111741 1.736831 　　 Jarque-Bera 0.698018 1.474443 Probability 0.705387 0.478441 　　 Observations 15 15 1b. Vẽ đồ thị phân tán của 2 chỉ số trên (với trục hòanh cho biến CPI) (Sử dụng Excel/Graph) 250 200 150 NYSE Series1 Linear (Series1) 100 50 0 0 50 100 150 CPI 1c. Ước lượng phương trình hồi quy tuyến tính sau: NYSEt = α + β CPIt + ut Dependent Variable: NYSE 　　　 -9-
http://www.facebook.com/DethiNEU Method: Least Squares 　 Date: 08/10/07 Time: 15:39 　 Sample: 1 15 　 Included observations: 15 　　　　　　 Variable Coefficient Std. Error t-Statistic Prob. 　　　　　 C -102.0606 23.76678 -4.294252 0.0009 CPI 2.129443 0.230284 9.247018 0.0000 　　　　　 R-squared 0.86803 Mean dependent var 112.5447 Adjusted R-squared 0.857879 S.D. dependent var 52.63217 S.E. of regression 19.8418 Akaike info criterion 8.937024 Sum squared resid 5118.059 Schwarz criterion 9.031431 Log likelihood -65.02768 F-statistic 85.50734 Durbin-Watson stat 0.603767 Prob(F-statistic) 0.00000 Dựa vào bảng kết quả hồi quy trên, ta có phương trình hồi quy tuyến tính: NYSEt = -102.0606 + 2.129443 CPIt + ut Chuyển số liệu sang Eview: Quick / Estimate Equation / nyse c cpi. 1d. Xác định khỏang tin cậy 95% cho hệ số độ đốc (β). Mức ý nghĩa α = 5% , α/2 = 0.025 Tra bảng t-student tn-2, α/2 = t13,0.025 = 2.16 Để xác định khỏang tin cậy cho hệ số độ dốc β, ta phải so sánh như sau: ˆ ˆ ˆ ˆ β - tn-2, α/2*se( β ) ≤ β ≤ β + tn-2, α/2*se( β )  2.129443 – 2.16*0.230284 ≤ β ≤ 2.129443 + 2.16*0.230284  1.632 ≤ β ≤ 2.626 Nhận xét: Khỏang tin cậy 95% (mức ý nghĩa α = 5%) cho thấy β> 0, CPI và NYSE có quan hệ tuyến tính đồng biến, có ý nghĩa về mặt thống kê. - 10 -
http://www.facebook.com/DethiNEU ˆ 1e. Vẽ đồ thị của đại lượng sai số ut theo CPIt (với u t trên trục tung) UT v s. CPI Số liệu chuyển từ Excel sang 40 Eview: View / Graph / Scatter / Scatter with Regression. 20 0 UT -20 -40 40 60 80 100 120 140 CPI Nhận xét: Nhìn vào đồ thị ta thấy các giá trị u^t dao động xung quanh đường t =0, khi CPI tăng, lúc đầu các giá trị t giảm dần, sau đó tăng dần. Câu 2: (Dữ liệu Gujarati 4 – Table 6.4) CM: số trẻ sơ sinh tử vong trên 1000 trẻ sơ sinh PGNP: GNP bình quân đầu người (USD) Chuyển dữ liệu sang phần mềm Eview. 2a. Viết phương trình hồi quy tổng thể (PRF) CMi = α+ β PGNPi + ui Bằng trực quan, kỳ vọng dấu của hệ số độ dốc trong phương trình hồi quy là d ấu (-) vì 2 bi ến này có mức độ tương quan nghịch nhau, không thể đồng nhau. Vì n ếu xét PGNP là bi ến đ ộc l ập, CM là biến giải thích thì khi PGNP tăng (hoặc gi ảm) dẫn đến CM cùng tăng (ho ặc gi ảm) gây ra tình trạng không hợp lý với thực tế. Trong thực tế không có tình trạng GNP bình quân đầu người tăng sẽ dẫn đến số trẻ sơ sinh tử vong tăng. 2b. Ước lượng phương trình hồi quy. Dependent Variable: CM 　　　　 Method: Least Squares 　 - 11 -
http://www.facebook.com/DethiNEU Date: 08/10/07 Time: 23:18 　 Sample: 1 64 　 Included observations: 64 　　　　　　 Variable Coefficient Std. Error t-Statistic Prob. 　　　　　 C 157.4244 9.845583 15.98935 0.0000 PGNP -0.011364 0.003233 -3.515661 0.0008 　　　　　 R-squared 0.166217 Mean dependent var 141.5 Adjusted R-squared 0.152769 S.D. dependent var 75.97807 S.E. of regression 69.93413 Akaike info criterion 11.36374 Sum squared resid 303228.5 Schwarz criterion 11.4312 Log likelihood -361.6396 F-statistic 12.35987 Durbin-Watson stat 1.931458 Prob(F-statistic) 0.000826 Sử dụng Eview : Quick / Estimate Equation / cm c pgnp. Dựa vào bảng kết quả này, ta nhận đựơc phương trình hồi quy: CMi = 157.4244 – 0.011364* PGNPi + u iˆ Kết quả của hệ số độ dốc đúng với kỳ vọng β= - 0.011364 Ý nghĩa: Hệ số độ dốc β: theo thông tin mẫu, nếu GNP bình quân đầu người tăng 1000USD thì trung bình CM số trẻ sơ sinh tử vong giảm 11 trẻ. Tung độ gốc α=157.4244 của phương trình hồi quy ước lượng không có giải thích. 2c. Xác định mối quan hệ tuyến tính có ý nghĩa về mặt thống kê với mức ý nghĩa α=5% giữa CM và PGNP. Đặt giả thiết, PGNP(X) và CM(Y) không có mối quan hệ tuyến tính v ề m ặt th ống kê (X không ảnh hưởng đến Y) H0: β = 0 H1: β # 0 Tại 2b, Ta đã có p-value = 0.0008
http://www.facebook.com/DethiNEU Các kết quả kiểm định khác không đổi. Câu 3. Cho kết quả phương trình hồi quy ước lượng Yt= 16898.27 – 2978.546 Xt Yt : lượng cầu hoa hồng (lố/quí) Xt : giá bán trung bình hoa hồng trong quí (10000/lố). 3a. Xác định độ co giãn trung bình của cầu hoa hồng: ε = dY/dX * X / Y = - 2978.546 * (3.106875/ 7645) = - 1.21046 Ý nghĩa: Theo thông tin mẫu, tại mức giá trung bình nếu giá bán hoa hồng trong quý tăng 1% thì l ượng cầu hoa hồng sẽ giảm 1.21%. 3b. Ước lượng hệ số tương quan r : Ta có: Sx = √?∑(Xi - X )2 / (n-1)  Sx2 = ∑( Xi - X )2 / (n-1)  ∑(Xi - X )2 = Sx2 * (n-1) = 0.5378072 * (16 – 1) = 4.338545539 ˆ β = ∑ xi*yi / ∑xi2 = ∑(Xi - X )*(Yi - Y ) / ∑(Xi - X )2 ˆ => ∑(Xi - X )*(Yi - Y ) = β * ∑(Xi - X )2 = - 2978.546 * 4.338545539 = - 12922.55746 Cov(X,Y) = (1/n-1)* ∑(Xi - X )*(Yi - Y ) = (1/16-1)* (-12922.55746) = -861.5038307 Vậy: r = Cov(X,Y) / Sx*Sy = -861.5038307 / (0.537807*2042.814) = -0.784155037 3c. Ước lượng giá trị của R2 (hệ số xác định). Do đặc điểm của hàm hồi quy đơn biến, ta có: R2 = r2 = (-0.784155037)2 = 0.614899122 - 13 -