Bài giảng Khoa học quản lý ứng dụng: Chương 3 - ThS. Huỳnh Đỗ Bảo Châu

2/12/2017<br /> <br /> Mục tiêu bài học<br /> <br /> TRƯỜNG ĐẠI HỌC NGÂN HÀNG TP<br /> .HCM<br /> KHOA HỆ THỐNG THÔNG TIN QUẢN LÝ<br /> <br /> <br /> <br /> KHOA HỌC QUẢN LÝ ỨNG DỤNG<br /> <br /> <br /> <br /> <br /> <br /> <br /> Trình bày đặc điểm của bài toán QHTT<br /> Phân biệt các dạng bài toán QHTT<br /> Ứng dụng cách xây dựng mô hình cho bài toán QHTT<br /> Sử dụng một số công cụ máy tính để giải bài toán QHTT<br /> Giải thích kết quả sau khi giải bài toán QHTT<br /> <br /> CHƯƠNG 3<br /> LẬP TRÌNH TUYẾN TÍNH (Linear Programming)<br /> GV. ThS. Huỳnh Đỗ Bảo Châu<br /> <br /> 1<br /> <br /> 2<br /> <br /> Nội dung chính<br /> 1.<br /> 2.<br /> 3.<br /> 4.<br /> 5.<br /> <br /> Các giả định cho quy hoạch tuyến tính<br /> <br /> Mô hình hóa bài toán QHTT<br /> Phương pháp đồ thị<br /> Giải pháp máy tính<br /> Phân tích độ nhạy<br /> Các mô hình ví dụ<br /> <br /> 3<br /> <br /> GV.ThS. Huỳnh Đỗ Bảo Châu<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> Các giá trị tham số là chắc chắn<br />  Không đổi theo quy mô<br /> VD: 1 sp thêm 4 $ lợi nhuận, đòi hỏi 3 giờ<br /> để sản xuất, vậy 500 sp thêm $ 4x500, cần<br /> 3x500 giờ<br />  Không có tương tác giữa các biến quyết định<br /> <br /> <br /> 4<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> 1<br /> <br /> 2/12/2017<br /> <br /> Giới thiệu về Bài toán QHTT<br /> Xác định x1, x2, …, xn sao cho:<br /> Cực đại (hay Cực tiểu) hàm mục tiêu Z:<br /> Z = z(x1, x2, …, xn)<br /> Đồng thời thỏa mãn các ràng buộc Rj:<br /> <br /> 1. Mô hình hóa bài toán QHTT<br /> <br /> Rj = rj(x1, x2, …, xn)<br /> Trong đó, z và rj là biểu thức tuyến tính<br /> đối với x1, x2, …, xn.<br /> <br /> 5<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> Các bước áp dụng kỹ thuật QHTT<br /> B1: Xác định vấn đề cần giải quyết mối quan hệ theo<br /> mô hình tuyến tính không.<br /> B2: Nếu là vấn đề không có cấu trúc, cần phân tích và<br /> xây dựng như 1 mô hình toán học<br /> B3: Giải mô hình và tìm ra kết quả bằng cách sử dụng<br /> các kỹ thuật toán học<br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> 6<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> Xây dựng mô hình QHTT<br /> Xác định:<br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> Số biến cần tìm<br /> Hàm mục tiêu ( MAX, hoặc  MIN)<br /> Các ràng buộc của các biến (các mối quan hệ tuyến tính)<br /> <br /> 2 kỹ thuật phổ biến là Đồ thị và Đơn hình.<br /> <br /> 7<br /> <br /> GV.ThS. Huỳnh Đỗ Bảo Châu<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> 8<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> 2<br /> <br /> 2/12/2017<br /> <br /> Các dạng bài toán QHTT<br /> <br /> <br /> Cực đại chuẩn<br /> <br /> ∑<br /> <br /> <br /> <br /> Ràng buộc:<br /> <br /> ∑<br /> <br /> ∀<br /> 0 ∀<br /> <br /> 1,2, … ,<br /> <br /> 1,2, …<br /> <br /> 0<br /> <br /> <br /> Cực tiểu chuẩn<br /> Ràng buộc:<br /> <br /> 2. Phương pháp đồ thị<br /> <br /> ∑<br /> <br /> <br /> ∑<br /> <br /> ∀<br /> 0 ∀<br /> <br /> 1,2, … ,<br /> <br /> 1,2, …<br /> <br /> 0<br /> <br /> <br /> Bài toán cực đại (hay cực tiểu) với ràng buộc có dấu ≥ và cả dấu ≤.<br /> <br /> 9<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> Phương pháp đồ thị<br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> <br /> Có nhiều ràng buộc dưới dạng bất phương trình<br /> Số biến cần tìm là 2<br /> <br /> Cung cấp bức tranh toàn cục về giải pháp bài toán.<br /> Thuận lợi để thực hiện phân tích độ nhạy.<br /> <br /> 11<br /> <br /> GV.ThS. Huỳnh Đỗ Bảo Châu<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> Giải bài toán QHTT bằng PP đồ thị<br /> <br /> Sử dụng khi:<br /> <br /> <br /> 10<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> <br /> <br /> Nghiệm khả dĩ (Feasible solution): 1 bộ giá trị các<br /> biến thỏa mãn các ràng buộc.<br /> Vùng khả dĩ (Feasible region): Tập tất cả các<br /> nghiệm khả dĩ.<br /> <br /> 12<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> 3<br /> <br /> 2/12/2017<br /> <br /> Các bước thực hiện (áp dụng cho bài toán 2 biến)<br /> <br /> <br /> <br /> <br /> B1: Biểu diễn các dữ kiện của bài toán dưới dạng phương<br /> trình hoặc bất phương trình<br /> B2: Giải các phương trình và bất phương trình bằng đồ thị,<br /> kết quả sẽ nhận được 1 vùng khả dĩ<br /> B3: Vẽ 1 đường thẳng biểu diễn hàm mục tiêu và tịnh tiến<br /> đường này tiến về miền nghiệm khả dĩ. Điểm đầu tiên mà<br /> đường hàm mục tiêu chạm với miền nghiệm chính là kết<br /> quả bài toán.<br /> <br /> 13<br /> <br /> Ví dụ minh họa<br /> (MÔ HÌNH BÀI TOÁN CỰC ĐẠI)<br /> <br /> <br /> <br /> <br /> GV. 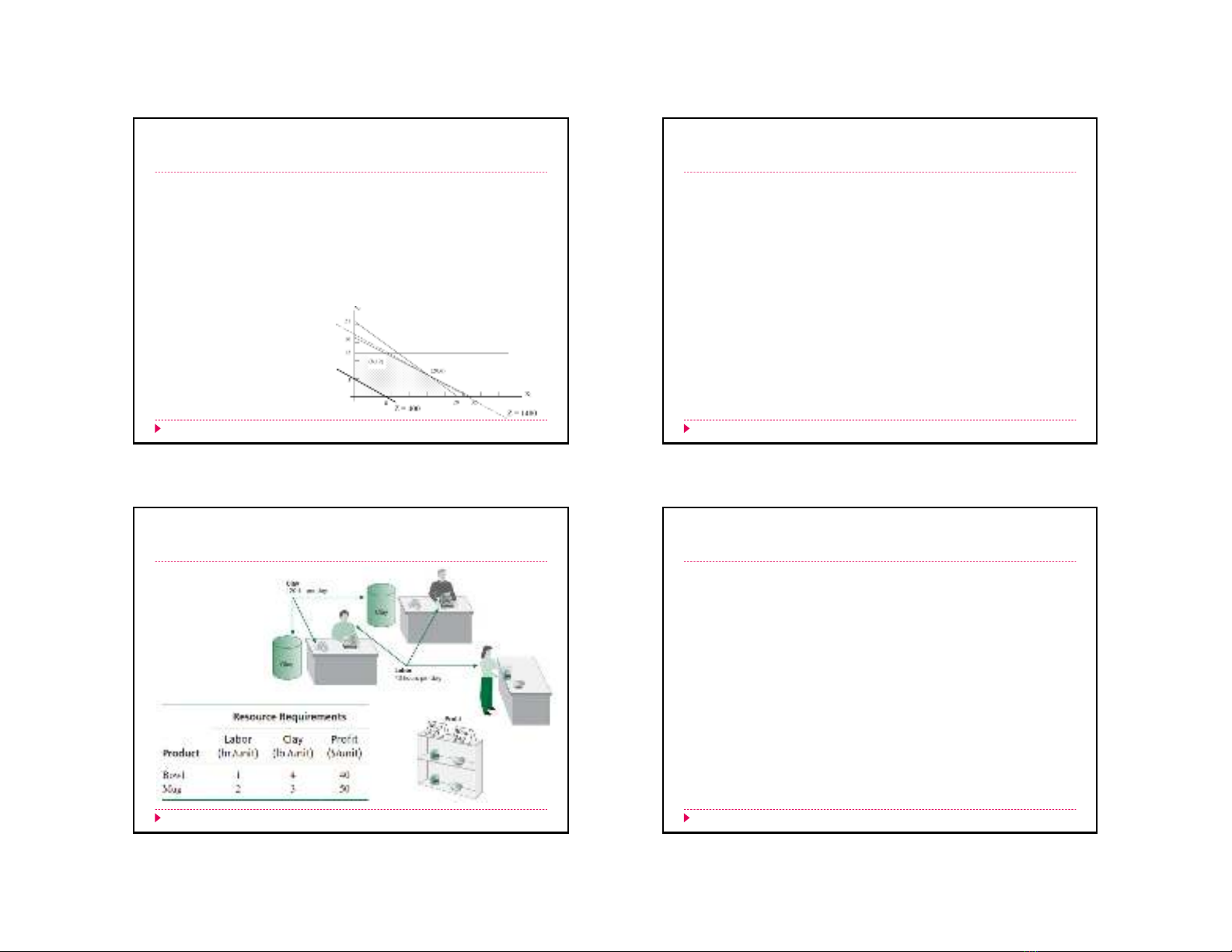Huỳnh Đỗ Bảo Châu<br /> <br /> Ví dụ minh họa (tt)<br /> <br /> Công ty Gốm Beaver Creek sản xuất thủ công quy mô<br /> nhỏ, sử dụng các nghệ nhân có tay nghề cao để sản<br /> xuất chén và ly bằng đất sét theo thiết kế và màu sắc<br /> của Mỹ. Hai nguồn lực chính của công ty là đất sét<br /> (clay), và lao động có tay nghề cao (labor).<br /> Với nguồn lực có hạn, công ty mong muốn biết bao<br /> nhiêu cái chén và ly cần sản xuất mỗi ngày để tối đa<br /> hóa lợi nhuận ?<br /> <br /> 14<br /> <br /> Ví dụ minh họa (tt)<br /> <br /> <br /> <br /> <br /> <br /> Gọi : số chén (bowl) cần sản xuất<br /> Gọi : số ly (mug) cần sản xuất<br /> HÀM MỤC TIÊU LỢI NHUẬN:<br /> 40<br /> 50 →<br /> RÀNG BUỘC:<br /> 2<br /> 40<br /> 1<br /> 3<br /> 120<br /> 4<br /> với<br /> <br /> 15<br /> <br /> GV.ThS. Huỳnh Đỗ Bảo Châu<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> 16<br /> <br /> ,<br /> <br /> 0, int<br /> <br /> GV. 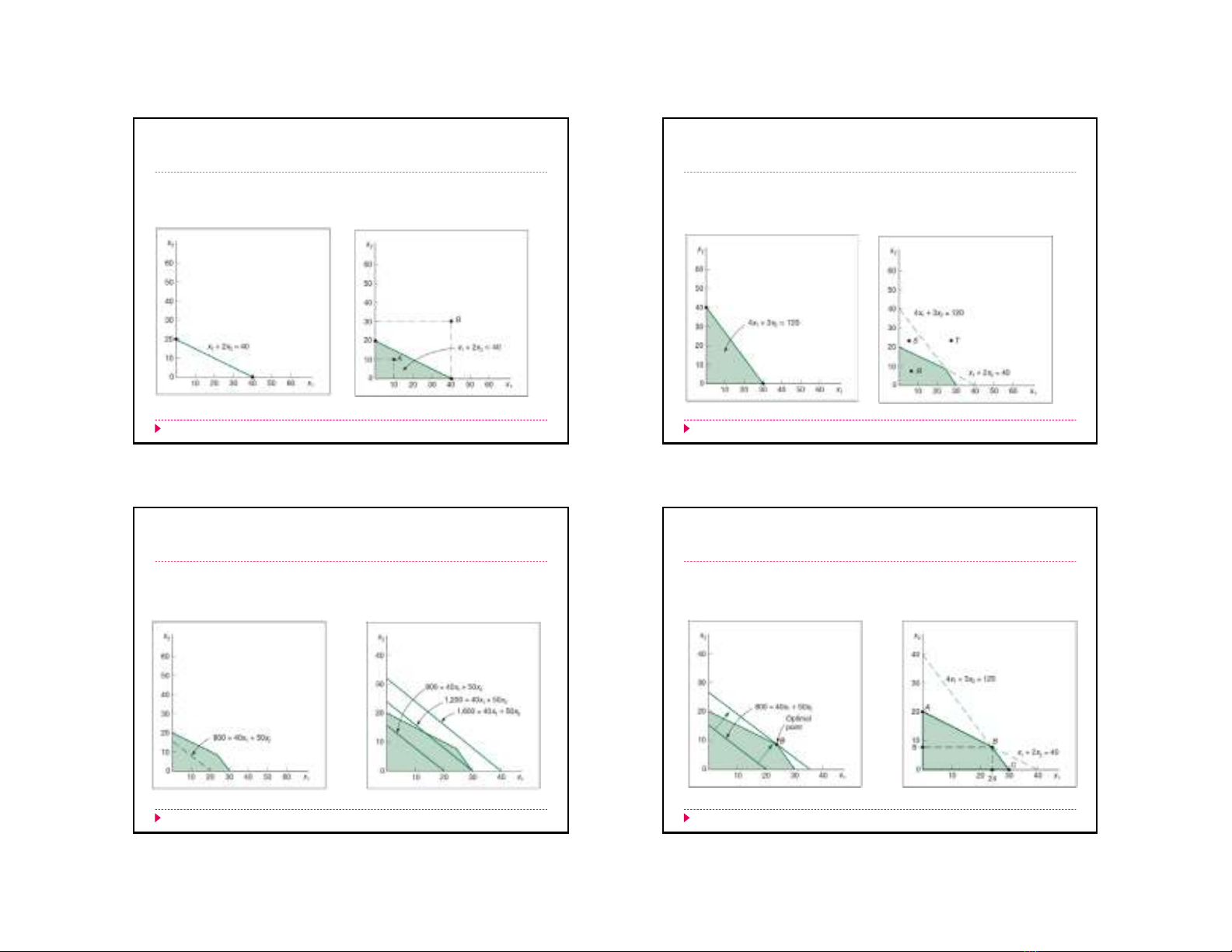Huỳnh Đỗ Bảo Châu<br /> <br /> 4<br /> <br /> 2/12/2017<br /> <br /> Ví dụ minh họa (tt)<br /> <br /> Ví dụ minh họa (tt)<br /> <br /> Đường biểu diễn ràng buộc về người lao động<br /> 1<br /> 2<br /> 40<br /> <br /> Đường biểu diễn ràng buộc về lượng đất sét nguyên liệu<br /> 4<br /> 3<br /> 120<br /> <br /> Vùng ràng buộc<br /> nguyên liệu đất sét<br /> <br /> Vùng ràng buộc<br /> nguồn lực lao động<br /> <br /> 17<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> Ví dụ minh họa (tt)<br /> <br /> <br /> 18<br /> <br /> <br /> <br /> Tìm giá trị của kết quả<br /> 24,<br /> <br /> Đường hàm mục tiêu<br /> với F = 800<br /> <br /> GV.ThS. Huỳnh Đỗ Bảo Châu<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> Ví dụ minh họa (tt)<br /> <br /> Vẽ đường hàm mục tiêu với giá trị F bất kỳ<br /> 50<br /> 40<br /> <br /> 19<br /> <br /> Kết hợp 2 ràng buộc<br /> có vùng khả dĩ<br /> <br /> ,<br /> 8 →<br /> <br /> 1.360<br /> Kết quả tại<br /> B (24,8)<br /> <br /> Tịnh tiến<br /> đường hàm mục tiêu<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> 20<br /> <br /> GV. Huỳnh Đỗ Bảo Châu<br /> <br /> 5<br /> <br />